笔试面试相关记录（5）

（1）给定一个字符串，含有大写、小写字母，空格，数字，需要将其变为满足如下条件：

所有的数字需要换成空格，并且字符串的头尾不包含空格，且整个字符串不包含连续的两个空格。

（2）给定n,k,L,R，接下拉n个数字，要从中选出某个序列，这个序列满足如下条件：

对于整个数组中的任意的k个连续的子数组，所选出的子序列必须包含子数组中的x个数字，其中x>=1 && x <= R；求所有满足条件的子序列的序列和（序列和就是序列中所有元素的数字相加）

示例

3 2 1 2

8 3 4 

输出48

（3）排雷：每次只能排去正方形的四个角的雷，如果雷的数目不够四个或者不在正方形的四个角，则不能排雷，输入数据为n行a b，其中a b表示雷的位置，求可以排雷的最大数目。

例如输入

8
0 0
0 1
1 0
1 1
2 0
2 1
10 0
10 1
输出4,最多可以拍雷四个。

（4）给定一个字符串如下3(a2(c))3(a)2(bc)，其中n(str)表示str出现n次，其中n > 0 && n < 10，将其还原为原始字符串。

#include 
#include 
#include 
#include 
using namespace std;

int main() {
    string str;
    while (cin >> str) { // 注意 while 处理多个 case
        int len = str.size();
        stack stk;
        int i = 0;
        while(i < len) {
            if (str[i] == ')') {
                string t;
                while (stk.top() != "(") {
                    t += stk.top();
                    stk.pop();
                }
                // 取出(
                stk.pop();
                // 取出数字
                // 3(a2(c)) 3(a) 2(bc)
                string n = stk.top();
                stk.pop();
                if (n.find_first_of("123456789") != string::npos) {
                    // 是数字
                    int times = n[0] - '0';
                    string orign = t;
                    for (int k = 0; k < times-1; k++) {
                        t += orign;
                    }
                } 
                if (stk.size()) {   
                    string c = stk.top();
                    if (c != "(") {
                        t = c + t;
                        stk.pop();
                    }   
                }
                stk.push(t);
                i++;
            } else {
                if (str[i] == '(') {
                    stk.push("(");
                    i++;
                } else if(isdigit(str[i])) {
                    stk.push(to_string(str[i]-'0'));
                    i++;
                } else {
                    string l = "";
                    while (isalpha(str[i])) {
                        l += str[i];
                        i++;
                    }
                    stk.push(l);
                }
            }
        }
        cout << stk.top() << endl;
    }
}

（5）给一串数字，例如 9 8 5 6 3 2 4 1 7 0，第一个数字表示后面数字的个数，后面的数字都不重复，求出最小的峰值数，如果没有就输出-1（峰值数表示其值比左右两边都大的数字）；

#include 
#include 
#include 
using namespace std;

int main() {
    string str;
    while (std::getline(std::cin, str)) { // 注意 while 处理多个 case
        int len = str.size();
        vector nums;
        int left = 0, t = 0;
        while (left < len) {
            if (isdigit(str[left])) {
                t = t*10 + (str[left]-'0');
            } else {
                nums.push_back(t);
                t = 0;
            }
            left++;
        }
        nums.push_back(t);
        // for (int i = 0; i < nums.size(); i++) {
        //     cout << nums[i] << "-";
        // }
        int min_head = 1e8;
        for (int i = 2; i < nums.size()-1; i++) {
            if (nums[i] > nums[i-1] && nums[i] > nums[i+1] && nums[i] < min_head) {
                min_head = nums[i];
            }
        }
        if (min_head == 1e8) {
            cout << -1 << endl;
        } else {
            cout << min_head << endl;
        }
    }
}

（6） 

    int a = 1;
    int &ra = a;
    int* pa = &a;
    int* pb = new int(a);
    a = 2;
    cout << *pa <<" " << *pb << endl;
    输出2 1

（7）

void func(char*) {
    cout << "char *" << endl;
}

void func(int) {
    cout << "int" << endl;
}
int main()
{
    func(nullptr);

    return 0;
}
输出char *

（8）

已知一个按照递增顺序排列的整数数组nums和一个目标值target，找出给定目标值在数组中的开始位置和结束位置。

要求：

1.时间复杂度O(log n)

2.空间复杂度O(1)

示例：

输入：nums=[3,5,5,8,8,8,10]，target=8

输出：[3,5]

输入：nums=[3,5,5,8,8,8,10]，target=9

输出：[-1,-1]

答题模板

class Solution {

public:

   vector searchRange(vector& nums, int target) {

   }

#include 
#include 

using namespace std;

int searchleft(vector& nums, int target) {
    int left = 0, right = nums.size()-1;
    while (left < right) {
        int mid = (left+right)>>1;
        if (nums[mid] >= target) {
            right = mid;
        } else {
            left = mid+1;
        }
    }
    if (nums[left] == target) return left;
    return -1;
}

int searchright(vector& nums, int target) {
    int left = 0, right = nums.size()-1;
    while(left < right) {
        int mid = (left+right)>>1;
        if (nums[mid] <= target) {
            left = mid+1;
        } else {
            right = mid-1;
        }
    }
    return left;
}

vector searchRange(vector& nums, int target) {
    int left = searchleft(nums, target);
    vector ans(2, 0);
    if (left == -1) {
        ans[0] = -1;
        ans[1] = -1;
        return ans;
    }
    int right = searchright(nums, target);
    ans[0] = left;
    ans[1] = nums[right] == target ? right:right-1;
    return ans;
}

int main() {
    vector nums{3, 5, 5, 8, 8, 8, 8, 10};
    int target = 3;
    vector ans = searchRange(nums, target);
    cout << ans[0] << " " << ans[1];
    system("pause");
    return 0;
}

（9）给你一个整数数组coins, 表示不同面额的硬币，以及一个整数amount，表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回-1。
你可以认为每种硬币的数量是无限的。
要求：时间复杂度O(Sn), S是金额，n是面额数

数值范围：
1 <= coins.length <= 12
0 <= amount <= 10^4

【测试用例】
输入：coins = [1, 2, 5], amount = 11
输出：3
输入：coins = [2], amount = 3
输出：-1
输入：coins = [1], amount = 0
输出：0

【参考函数】
int coinChange(vector& coins, int amount) {}

#include 
#include 

using namespace std;

int coinChange(vector& coins, int amount) {
    vector dp(amount+1, 1e9);
    // 总价为0时，需要0张
    dp[0] = 0;
    int len = coins.size();
    for (int i = 0; i < len; i++) {
        for (int j = coins[i]; j <= amount; j++) {
            dp[j] = min(dp[j], dp[j-coins[i]] + 1);
        }
    }
    if (dp[amount] == 1e9) {
        return -1;
    }
    return dp[amount];
}

int main() {
    vector coins{1,2,5};
    int amount = 11;
    cout << coinChange(coins, amount);
    system("pause");
    return 0;
}

（10）

你参与了一个微信小游戏的研发，策划同学计划给你发布n项任务，每项任务会有一个 发布时间点r 和 预估处理时长p ，你需要等待任务发布后才能开始编码实现，同时每项任务都会有一位测试同学跟进测试工作，你需要合理安排工作，让所有测试同学等待的时间之和最少，此外你作为一个资深的程序员，多项任务可以交替进行。
输入：n r1 p1 ... rn pn
输出：各项任务的任务id和完成时间，任务id从下标1开始，按完成时间升序排列
比如
输入：2 1 4 3 1
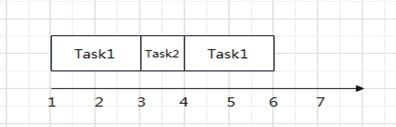
即发布2项任务，任务1的发布时间点r=1，处理时长p=4；任务2的发布时间点r=3，处理时长p=1，合理的工作安排如下图所示:

输出：
2 4
1 6
测试同学等待的总时长为10
                                                        

【测试用例】
输入：2 1 4 3 1
输出：
2 4
1 6
输入：3 3 3 4 1 1 7
输出：
2 5
1 7
3 12
输入：2 5 2 3 1
输出：
2 4
1 7
【题目1】请简要阐述解题思路（12分）
【题目2】编写相应的程序实现（24分）
【参考函数】
struct Task {
   int i;          // 任务id
   int r, p;       // 发布时间，处理时长
};
vector> processTasks(vector& tasks) {}

思路：按照结束时间最早进行排序，这个时候的顺序就是最终的任务执行的顺序，因为多项任务交替进行，每一个任务都有一个测试人员，要让所有测试人员等待最小的时间，需要让 能够最先完成的任务最先完成，如果最先完成的没有在最开始完成，那么它带来的延迟会加到其他所有的测试人员上。（个人思路，不确定是不是正确的）

 

#include 
#include 
#include 
using namespace std;

struct Task {
    int i;
    int r, p;
};

static bool cmp(Task& t1, Task& t2) {
    return t1.r + t1.p < t2.r + t2.p;
}

vector> processTasks(vector& tasks) {
    int last_start = tasks[0].r;
    vector> ans;
    int len = tasks.size();
    // 此时第一个任务就是最先完成的任务，直接放入ans中
    ans.push_back({tasks[0].i, tasks[0].r + tasks[0].p});
    // 遍历剩下的任务
    for (int i = 1; i < len; i++) {
        // 分三种情况
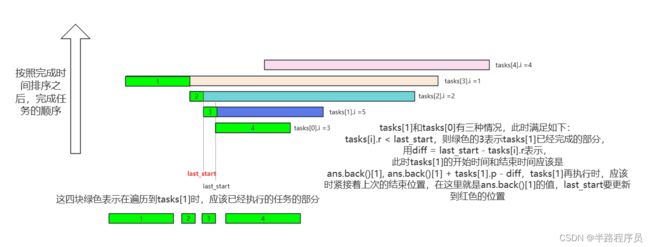
        if (tasks[i].r < last_start) {
            int diff = last_start - tasks[i].r;
            last_start = tasks[i].r;
            ans.push_back({tasks[i].i, ans.back()[1] + tasks[i].p - diff});
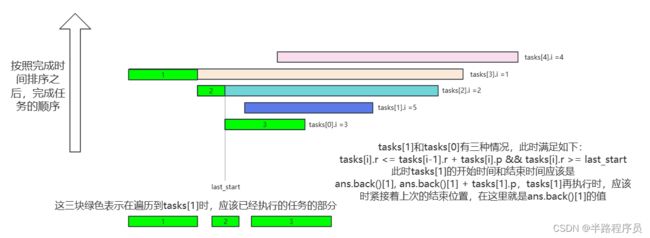
        } else if (tasks[i].r > tasks[i-1].r + tasks[i].p) {
            ans.push_back({tasks[i].i, ans.back()[1] + tasks[i].p});
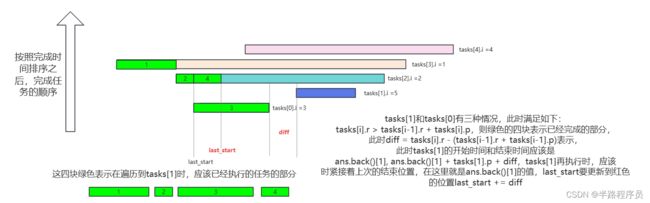
        } else {
            int diff = tasks[i].r - (tasks[i-1].r + tasks[i-1].p);
            last_start += diff;
            ans.push_back({tasks[i].i, ans.back()[1] + diff + tasks[i].p});
        }
    }
    return ans;
}

int main() {
    int n;
    cin >> n;
    vector tasks(n);
    for (int i = 0; i < n; i++) {
        cin >> tasks[i].r;
        cin >> tasks[i].p;
        tasks[i].i = i+1;
    }
    sort(tasks.begin(), tasks.end(), cmp);

    // for (int i = 0; i < n; i++) {
    //     cout << tasks[i].r << " " << tasks[i].p << endl;
    // }
    
    vector> ans = processTasks(tasks);
    for (int i = 0; i < ans.size(); i++) {
        cout << ans[i][0] << " " << ans[i][1] << endl;
    }
    
    system("pause");
    return 0;
}