二叉树经典OJ题——【数据结构】

W...Y的主页 

代码仓库分享  

---

今天我们来进行二叉树的OJ练习，就是利用二叉树的前序、中序、后续以及晨序遍历的特性进行OJ训练。话不多说，来看我们的第一道题。

【leetcode 965.单值二叉树】

OJ链接 

如果二叉树每个节点都具有相同的值，那么该二叉树就是单值二叉树。

只有给定的树是单值二叉树时，才返回 true；否则返回 false。

示例 1：

输入：[1,1,1,1,1,null,1]
输出：true

示例 2：

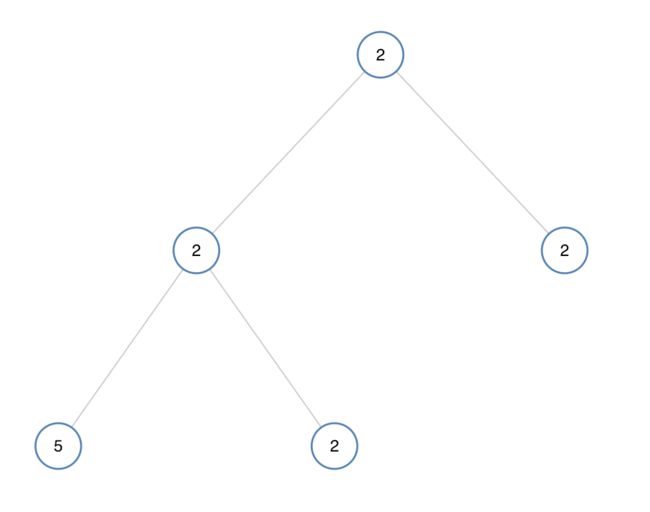
输入：[2,2,2,5,2]
输出：false

题目函数接口：

root：二叉树的根节点指针。 返回值：bool类型（真 true 假 false）

---

给定一个二叉树，我们需要判断树中val的值是不是相同的。我们的思路就是将其全部遍历一遍，如果在遍历过程中发现其中有一个数与其余数不同即可停止，返回false，反之返回true

强调一下：数与数之间是有传递性的，所以我们不需要将其遍历时先创建一个变量将val值进行标记。a = b,b=c,那么a=c。

代码实现：

bool isUnivalTree(struct TreeNode* root){
    if(root == NULL)
    {
        return true;
    }
    if(root->left != NULL && root->left->val != root->val)
    {
        return false;
    }
    if(root->right != NULL && root->right->val != root->val)
    {
        return false;
    }
    return isUnivalTree(root->left) && isUnivalTree(root->right);
}

当我们root等于空时，满足题中要求，所以要返回true。当root的左子树不为空并且左子树的val值，不等于其父节点val值则返回false，同理root的右子树不为空且右子树的val值不等于其父节点val值则返回flase。最后我们进行一个递归遍历，将树中的所有节点全部遍历一遍即可，如果有一个返回false，则最终返回false。左子树与右子树必须全部为true才真正为true

这个函数的原理其实就是前序遍历的变形。

我们简单画一张递归分析图：

【leetcode 100.相同的树】 

OJ链接

给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

示例 1：

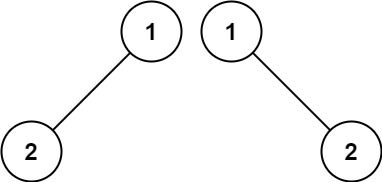
输入：p = [1,2,3], q = [1,2,3]
输出：true

示例 2：

输入：p = [1,2], q = [1,null,2]
输出：false

示例 3：

输入：p = [1,2,1], q = [1,1,2]
输出：false

题目函数接口：

p：一棵树的根节点指针。q：另一颗树的根节点指针

---

这道题给予我们两个树，让我们检查两颗树是否相同。

我们就是模仿遍历。当我们遍历一棵树的左子树时，另一颗树也遍历其左子树。右子树同理即可。（如同模仿者一样同步进行）

大概思路已经确定，下面就是细节了。

当两棵树的节点都为NULL，我们返回true。当两棵树的节点一个为空，另一个不为空，我们返回false。当两个节点的val值不相同时，我们也返回空。

bool isSameTree(struct TreeNode* p, struct TreeNode* q){
    if(p == NULL && q == NULL)
        return true;
    if(p == NULL || q == NULL)
        return false;
    if(p->val != q->val)
        return false;
    return isSameTree(p->left, q->left)&&isSameTree(p->right, q->right);
}

和上面的题递归类型基本相同，先递归左树再递归右树，只有两个树递归完成后返回值都为true才为true。

【leetcode 101.对称二叉树】

OJ链接 

给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例 1：

​

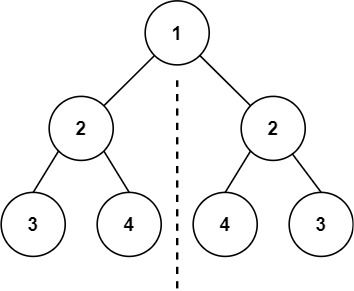
输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

​

输入：root = [1,2,2,null,3,null,3]
输出：false

题目函数接口：

root：二叉树的根节点。bool：bool类型（真 true 假 false）

---

这道题与leetcode 100.相同的树做法非常相似，就是一道变形题。它将两颗树变成一棵树，然后考察这棵树是否对称。

我们可以继续依照上题，一棵树看作两棵树，但是这两个树的根节点都为root。然后进行遍历判断。因为是判断树是否对称，所以两个指针应该一个遍历左树，一个遍历右数，然后检查每个节点的val是否相等即可。

代码演示：

bool checkroot(struct TreeNode* p, struct TreeNode* q){
    if(p == NULL && q == NULL)
        return true;
    if(p == NULL || q == NULL)
        return false;
    if(p->val != q->val)
        return false;
    return checkroot(p->left, q->right)&&checkroot(p->right, q->left);
}
bool isSymmetric(struct TreeNode* root){
   return checkroot(root, root);
}

注意：这道题的return checkroot(p->left, q->right)&&checkroot(p->right, q->left);是左树与右树进行比较，与上一题的return值不同。

为了更好的理解，递归展开图：

【leetcode 572. 另一颗子树】

OJ链接 

给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。

二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。

示例 1：

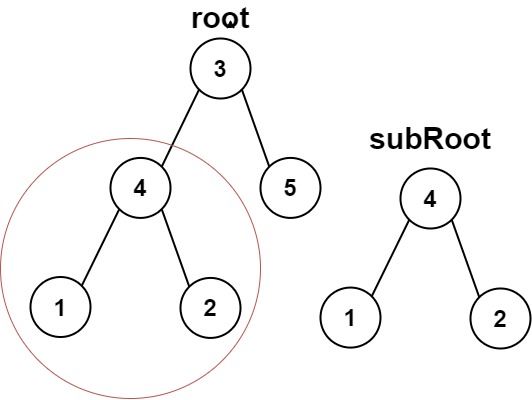
输入：root = [3,4,5,1,2], subRoot = [4,1,2]
输出：true

示例 2：

输入：root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
输出：false

题目函数接口：

root： 大树的根节点。 suboot：小树的根节点。

---

这道题我们将大树中可以分解成一颗颗与小树结构相同的树，然后遍历比较即可。依旧是leetcode100.相同的树的变形。

代码展示：

bool isSameTree(struct TreeNode* p, struct TreeNode* q){
    if(p == NULL && q == NULL)
        return true;
    if(p == NULL || q == NULL)
        return false;
    if(p->val != q->val)
        return false;
   return isSameTree(p->left, q->left)&&isSameTree(p->right, q->right);
}

bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
    if(root == NULL)
    {
        return false;
    }
    
    if(isSameTree(root, subRoot))
    {
        return true;
    }
    return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
}

 【leetcode 104.二叉树的最大深度】

OJ链接

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：3

示例 2：

输入：root = [1,null,2]
输出：2

---

要想找到二叉树的最大深度，我们必须用深度优先遍历，前中后序都可以。将树进行遍历，每进入一颗子树就进行计数+1。

代码演示：

int maxDepth(struct TreeNode* root){
    if(root == NULL)
    {
        return 0;
    }
    int val1 = 0, val2 = 0;
    val1 =  maxDepth(root->left);
    val2 = maxDepth(root->right);
    

    return val1 >= val2 ? val1+1 : val2+1;
}

注意：我们必须再函数中创建临时变量用来接收递归函数每次的返回值。

遍历左树与右数，谁的值大（树的深度深）就返回谁。

【leetcode 树的前中后遍历】——这是三道题

前序：OJ链接

中序：OJ链接

后序： OJ链接

给你二叉树的根节点 root ，返回它节点值的 前序 遍历。

示例 1：

输入：root = [1,null,2,3]
输出：[1,2,3]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

示例 4：

输入：root = [1,2]
输出：[1,2]

示例 5：

输入：root = [1,null,2]
输出：[1,2]

题目函数接口：

root：是目标二叉树的根。returnSize：因为函数只能返回一个值，所以这个参数是动态开辟的数组长度。 int*：返回数组的地址。

---

这里的前序遍历不仅仅只是前序遍历，而是将前序遍历的数全部放入数组中去。

所以我们必须开辟动态数组将其数放入。那么我们首先的任务就是得求出二叉树中的所有节点个数。

我们创建一个函数，然后进行前序遍历计数，返回一棵树的节点个数。

int TreeSize(struct TreeNode* root)
 {
     return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
 }

然后我们动态开辟空间，然后遍历树将树中的每个节点的val值放入数组中。创建一个int变量记录数组角标，每放一个变量++。最后返回数组地址即可。

代码演示：

void preorder(struct TreeNode* root, int* a, int* i)
 {
     if(root == NULL)
     {
         return;
     }
     a[(*i)++] = root->val;
     preorder(root->left, a, i);
     preorder(root->right, a, i);
 }
int* preorderTraversal(struct TreeNode* root, int* returnSize){
    int n = TreeSize(root);
    int* a = (int*)malloc(sizeof(int)*n);

    int j = 0;
    preorder(root, a, &j);

    *returnSize = n;
    return a;
}

注意：我们创建的变量进行调用时应该传入地址，而不是单纯的值。因为如果传入对应的值，在每次调用函数时这个值不会累记，在调用函数结束后i会跟着销毁。

---

中序与后序与前序基本相同，只有三行代码调整了一下顺序。因为遍历顺序不同。

下面是代码展示：

中序：

int Treesize(struct TreeNode* root)
 {
     return root == NULL ? 0 :Treesize(root->left) + Treesize(root->right) + 1;
 }
 void InOrder(int* a, struct TreeNode* root, int* j)
 {
     if(root == NULL)
     {
         return;
     }
     InOrder(a, root->left, j);
     a[(*j)++] = root->val;
     InOrder(a, root->right, j);
    
 }
int* inorderTraversal(struct TreeNode* root, int* returnSize){
    int size = Treesize(root);
    int* a = (int*)malloc(sizeof(int) * size);
    int j = 0; 
    InOrder(a, root, &j);
    *returnSize = size;
    return a;
}

后序：

int Treesize(struct TreeNode* root)
 {
     return root == NULL ? 0 :Treesize(root->left) + Treesize(root->right) + 1;
 }
 void PostOrder(int* a, struct TreeNode* root, int* j)
 {
     if(root == NULL)
     {
         return;
     }
     PostOrder(a, root->left, j);
     PostOrder(a, root->right, j);
    a[(*j)++] = root->val;
 }
int* postorderTraversal(struct TreeNode* root, int* returnSize){
    int size = Treesize(root);
    int* a = (int*)malloc(sizeof(int) * size);
    int j = 0; 
    PostOrder(a, root, &j);
    *returnSize = size;
    return a;
}

【牛客网 KY11 二叉树遍历】

OJ链接 

描述：

编一个程序，读入用户输入的一串先序遍历字符串，根据此字符串建立一个二叉树（以指针方式存储）。 例如如下的先序遍历字符串： ABC##DE#G##F### 其中“#”表示的是空格，空格字符代表空树。建立起此二叉树以后，再对二叉树进行中序遍历，输出遍历结果。

输入描述：

输入包括1行字符串，长度不超过100。

输出描述：

可能有多组测试数据，对于每组数据， 输出将输入字符串建立二叉树后中序遍历的序列，每个字符后面都有一个空格。 每个输出结果占一行。

示例1

输入：

abc##de#g##f###

输出：

c b e g d f a 

---

这道题不是接口题，所以我们就要自己动手创建二叉树。从main函数走起。

首先我们得了解题意，有一串字符数组是按照二叉树前序遍历出来的。我们就要将其建立成正常二叉树，然后再使用中序遍历将其一一打印出来即可。

注意：’#‘代表的是空格，也就是NULL。

我们使用示例1先来推测出二叉树的基本样子：

其实只要给我们前序遍历的树，我们就可以推测出二叉树的样子。

然后就是我们先创建出二叉树的结构体：

typedef struct BinaryTreeNode
{
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
	int val;
}BTNode;

就应该写主函数了，先创建一个数组进行存储写入数据，然后就得创建一个可以将数组变成二叉树的函数CreatTree，参数我们传入字符数组和角标i，调用函数一定要传入i的指针！！

如果遇到’#‘就直接返回NULL，如果不是NULL就malloc一个节点进行存储，然后让i++。继续递归出左子树与右子树。

最后再创建一个可以中序遍历的树调用打印即可。

完整代码如下：

#include 
#include
typedef struct BinaryTreeNode
{
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
	int val;
}BTNode;

BTNode* CreateTree(char* str, int *pi)
{
    if(str[*pi] == '#')
    {
        ++(*pi);
        return NULL;
    }
    BTNode* root = (BTNode*)malloc(sizeof(BTNode));
    root->val = str[*pi];
    (*pi)++;
    root->left = CreateTree(str,pi);
    root->right = CreateTree(str, pi);

    return root;
}
void Inorder(BTNode* root)
{
    if(root == NULL)
    {
        return;
    }
    Inorder(root->left);
    printf("%c ", root->val);
    Inorder(root->right);
}
int main() {
    char str[100];
    scanf("%s", str);
    int i = 0;
    BTNode* root = CreateTree(str, &i);
    Inorder(root);
    return 0;
}

以上就是经典二叉树的OJ习题分享，希望对大家有所帮助。

觉得帮助到了你，就给博主一个三连关注吧！！！