数据结构与算法:排序算法(2)
目录
堆排序
使用步骤
代码实现
计数排序
适用范围
过程
代码实现
排序优化
桶排序
工作原理
代码实现
堆排序
二叉堆的特性:
1. 最大堆的堆顶是整个堆中的最大元素
2. 最小堆的堆顶是整个堆中的最小元素
以最大堆为例,如果删除一个最大堆的堆顶(并不是完全删除,而是跟末尾的节点交换位置),经过自我调整,第2大的元素就会被交换上来,成为最大堆的新堆顶
在删除值为10的堆顶节点后,经过调整,值为9的新节点就会顶替上来;由于二叉堆的这个特性,每一次删除旧堆顶,调整后的新堆顶都是大小仅次于旧堆顶的节点。那么只要反复删除堆顶,反复调整二叉堆,所得到的集合就会成为一个有序集合。
使用步骤
1. 把无序数组构建成二叉堆。需要从小到大排序,则构建成最大堆;需要从大到小排序,则构建成最小堆
2. 循环删除堆顶元素,替换到二叉堆的末尾,调整堆产生新的堆顶
代码实现
public static void main(String[] args){
int[] array = new int[] {4,4,6,5,3,2,8,1,7,5,6,0,10};
heapSort(array);
System.out.println(Arrays.toString(array));
}
public static void downAdjust(int[] array, int parentIndex, int length) {
int temp = array[parentIndex];
int childIndex = 2 * parentIndex + 1;
while (childIndex < length){
if (childIndex + 1 < length && array[childIndex + 1] > array[childIndex]) {
childIndex++;
}
if (temp >= array[childIndex]){
break;
}
array[parentIndex] = array[childIndex];
parentIndex = childIndex;
childIndex = 2 * childIndex + 1;
}
array[parentIndex] = temp;
}
public static void heapSort(int[] array) {
//1.无序数组构建成最大堆
for (int i = (array.length-2)/2; i >= 0; i--) {
downAdjust(array, i, array.length);
}
System.out.println(Arrays.toString(array));
//2.环删除堆顶元素,移到集合尾部,调整堆产生新的堆顶
for (int i = array.length - 1; i > 0; i--) {
int temp = array[i];
array[i] = array[0];
array[0] = temp;
downAdjust(array, 0, i);
}
}计数排序
有一些特殊的排序并不基于元素比较,而是利用数组下标来确定元素的正确位置的。
适用范围
它适用于一定范围内的整数排序。在取值范围不是很大的情况下,它的性能甚至快过那些时间复杂度为O(nlogn)的排序
过程
假设数组中有20个随机整数,取值范围为0~10,要求用最快的速度把这20个整数从小到大进行排序,可以根据这有限的范围,建立一个长度为11的数组。数组下标从0到10,元素初始值全为0
随机值:9,3,5,4,9,1,2,7,8,1,3,6,5,3,4,0,10,9 ,7,9
这个无序的随机数列,每一个整数按照其值对号入座,同时,对应数组下标的元素进行加1操作
该数组中每一个下标位置的值代表数列中对应整数出现的次数;直接遍历数组,输出数组元素的下标值,元素的值是几,就输出几次,输出的数列已经是有序的了
代码实现
public static void main(String[] args){
int[] array = new int[] {4,4,6,5,3,2,8,1,7,5,6,0,10};
int[] sortedArray = countSort(array);
System.out.println(Arrays.toString(sortedArray));
}
public static int[] countSort(int[] array) {
//1.得到数列的最大值
int max = array[0];
for(int i=1; i max){
max = array[i];
}
}
//2.根据数列最大值确定统计数组的长度
int[] countArray = new int[max+1];
//3.遍历数列,填充统计数组
for(int i=0; i 排序优化
只以数列的最大值来决定统计数组的长度,其实并不严谨;如:数列的最大值是99,但最小的整数是90。如果创建长度为100的数组,那么前面从0到89的空间位置就都浪费了
解决:
以数列最大值-最小值+1作为统计数组的长度
同时,数列的最小值作为一个偏移量,用于计算整数在统计数组中的下标
public static void main(String[] args){
int[] array = new int[] {4,4,6,5,3,2,8,1,7,5,6,0,10};
int[] sortedArray = countSort(array);
System.out.println(Arrays.toString(sortedArray));
}
public static int[] countSort(int[] array) {
//1.得到数列的最大值和最小值,并算出差值d
int max = array[0];
int min = array[0];
for(int i=1; i max){
max = array[i];
}
if(array[i] < min){
min = array[i];
}
}
int d = max - min;
//2.创建统计数组并统计对应元素的个数
int[] countArray = new int[d+1];
for(int i=0; i=0;i--) {
sortedArray[countArray[array[i]-min]-1]=array[i];
countArray[array[i]-min]--;
}
return sortedArray;
} 桶排序
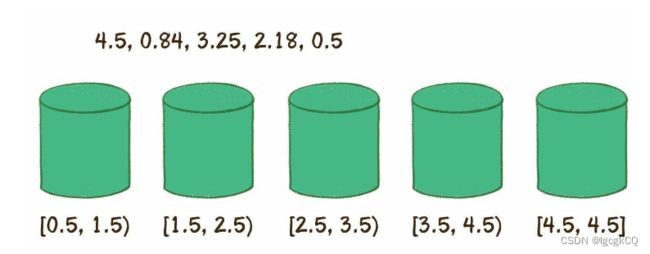
桶排序是一种线性时间的排序算法。类似于计数排序所创建的统计数组,桶排序需要创建若干个桶来协助排序。
桶:每一个桶(bucket)代表一个区间范围,里面可以承载一个或多个元素。
工作原理
1.创建桶,并确定每一个桶的区间范围
创建的桶数量等于原始数列的元素数量
区间跨度 = (最大值-最小值)/ (桶的数量 - 1)
2.遍历原始数列,把元素对号入座放入各个桶中
3.对每个桶内部的元素分别进行排序
4.遍历所有的桶,输出所有元素
代码实现
public static void main(String[] args){
double[] array = new double[]{4.12,6.421,0.0023,3.0,2.123,8.122,4.12, 10.09};
double[] sortedArray = bucketSort(array);
System.out.println(Arrays.toString(sortedArray));
}
public static double[] bucketSort(double[] array){
//1.得到数列的最大值和最小值,并算出差值d
double max = array[0];
double min = array[0];
for(int i=1; i max){
max = array[i];
}
if(array[i] < min){
min = array[i];
}
}
double d = max - min;
//2.初始化桶
int bucketNum = array.length;
ArrayList> bucketList = new ArrayList>(bucketNum);
for(int i=0;i());
}
//3.遍历原始数组,将每个元素放入桶中
for(int i = 0; i < array.length; i++){
int num = (int)((array[i] - min) * (bucketNum-1) / d);
bucketList.get(num).add(array[i]);
}
//4.对每个桶内部进行排序
for(int i = 0; i < bucketList.size(); i++){
Collections.sort(bucketList.get(i));
}
//5.输出全部元素
double[] sortedArray = new double[array.length];
int index = 0;
for(LinkedList list : bucketList){
for(double element : list){
sortedArray[index] = element;
index++;
}
}
return sortedArray;
} 所有的桶都保存在ArrayList集合中,每一个桶都被定义成一个链表(LinkedList