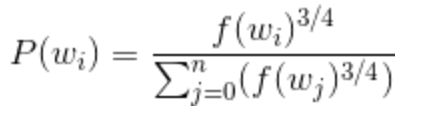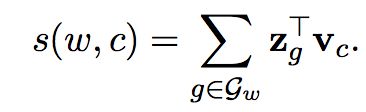Intro to Wordembedding
Intro to Wordembedding
background
wordembedding发展史上一个比较大的跨越就是Distributional Semantics，即用一个词的上下文去做一个词的表义，拥有相似上下文的词拥有相似的表义。
wordembedding in word2vec
word2vec原理
eg. I wanna train wordembedding with given training data.
- CBOW: 取窗口大小为2，则用
wannatrainwithgiven为输入，wordembedding为输出 - Skipgram：取窗口大小为2，则用
wordembedding为输入，wannatrainwithgiven为输出
本文仅以Skipgram为例，CBOW和Skipgram差异并不大。Skipgram需要最大化给定输入词，预测给定窗口里词的概率，即
传统会以简单的对输出做一个Softmax，即
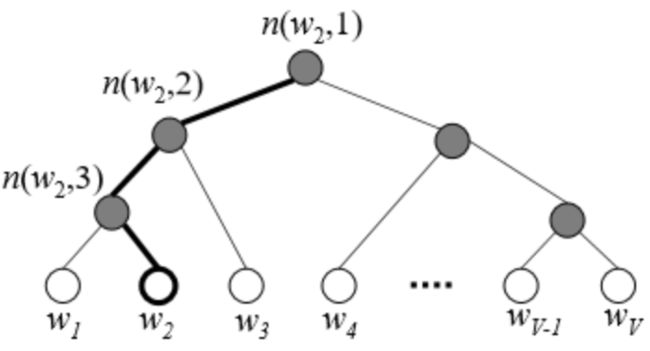
但是这样计算的时间复杂度会很高，即word2vec默认使用Hierarchical Softmax的方式做计算，即对训练词表生成一棵Huffman树，即
More precisely, each word w can be reached by an appropriate path from
the root of the tree. Let n(w, j) be the j-th node on the path from the
root to w, and let L(w) be the length of this path, so n(w, 1) = root
and n(w, L(w)) = w. In addition, for any inner node n, let ch(n) be an
arbitrary fixed child of n and let [x] be 1 if x is true and -1 otherwise.
则时间复杂度变为：
其中C为窗口大小，D为embedding的dimension，V为output dimension。
Negtive Sampling:
Unigram Distribution:
对于这个玩意我Google了一下，没有比较明确的搜索结果，所以写了一段代码做了一个简单的试验，随机K个字母，取样本P，对于字母A在K中的概率为Pk，在P中的概率为Pp，以Unigram Distribution，去指数0.1，0.75，0.80得到的概率为Pu0.1，Pu0.75，Pu0.8，Pu0.75相比其他值和Pp更接近于PK。我理解的是，对于wordembedding的语料来说，永远是真实全集的一个观测集，以Unigram Distribution表示要更好一些。代码如下：
int main(int argc, char **argv) {
unsigned long long next_random = (long long)1000;
vector all;
vector part;
int total = 10000000;
double f = 0.8;
for (int i = 0; i < total; ++i) {
next_random = next_random * (unsigned long long)25214903917 + 11;
all.push_back(next_random % 26 + int('A'));
}
int count = 0;
for (int i = 0; i < total; ++i) {
if (all[i] == int('A')) {
++count;
}
}
cout << "real prop of A: " << double(count) / total << endl;
unsigned seed = 100;
shuffle(all.begin(), all.end(), std::default_random_engine(seed));
for (int i = 0; i < total / 2; ++i) {
part.push_back(all[i]);
}
map cnt_map;
for (int i = 0; i < total / 2; ++i) {
if (cnt_map.find(part[i]) == cnt_map.end()) {
cnt_map[part[i]] = 0;
}
cnt_map[part[i]]++;
}
double sm = 0.;
for (auto &it : cnt_map) {
sm += pow(double(it.second), f);
}
cout << "part real prop of A: " << cnt_map[int('A')] / double(total / 2) << endl;
cout << "part noise prop of A: " << pow(double(cnt_map[int('A')]), f) / sm << endl;
return 0;
}
SubSampling:
其实代码里实现是这样的，或许是为了实现上的方便吧。
if (sample > 0) {
real ran = (sqrt(vocab[word].cn / (sample * train_words)) + 1) * (sample * train_words) / vocab[word].cn;
next_random = next_random * (unsigned long long)25214903917 + 11;
if (ran < (next_random & 0xFFFF) / (real)65536) continue;
}
subsampling的目的就是为了去除一些可能的无意义的高频词，例如the and for等等。
word2vec实现
- 用简单的hash表存储词，一个hash vector，一个word vector，数据读取时会不断的调整hash表大小来节省内存空间，其一是hash表达到总量70%是去调词频为1的词，然后扩容，第二次扩容去调词频为2的，依次增加，后续会再做一次参数指定的最小词频的词过滤，会再次对hash表做调整。简而言之，稀有词会被从词表里去掉。往往对于某个具体的场景来说，稀有词往往会是一个keyword，这样就要求wordembedding训练的数据量非常大，减少稀有词数量，这样用作基础的embedding，也会更合适。fasttext通过另一种方式解决了这个问题。
其实最后计算的时候用的是word的hash值，其实并没有很明显的one-hot的vector表示，在计算上是没有必要的。
- 用Huffman树表示词，非常惊艳的一段代码
205 // Create binary Huffman tree using the word counts
206 // Frequent words will have short uniqe binary codes
207 void CreateBinaryTree() {
208 long long a, b, i, min1i, min2i, pos1, pos2, point[MAX_CODE_LENGTH];
209 char code[MAX_CODE_LENGTH];
210 long long *count = (long long *)calloc(vocab_size * 2 + 1, sizeof(long long));
211 long long *binary = (long long *)calloc(vocab_size * 2 + 1, sizeof(long long));
212 long long *parent_node = (long long *)calloc(vocab_size * 2 + 1, sizeof(long long));
213 for (a = 0; a < vocab_size; a++) count[a] = vocab[a].cn;
214 for (a = vocab_size; a < vocab_size * 2; a++) count[a] = 1e15;
215 pos1 = vocab_size - 1;
216 pos2 = vocab_size;
217 // Following algorithm constructs the Huffman tree by adding one node at a time
218 for (a = 0; a < vocab_size - 1; a++) {
219 // First, find two smallest nodes 'min1, min2'
220 if (pos1 >= 0) {
221 if (count[pos1] < count[pos2]) {
222 min1i = pos1;
223 pos1--;
224 } else {
225 min1i = pos2;
226 pos2++;
227 }
228 } else {
229 min1i = pos2;
230 pos2++;
231 }
232 if (pos1 >= 0) {
233 if (count[pos1] < count[pos2]) {
234 min2i = pos1;
235 pos1--;
236 } else {
237 min2i = pos2;
238 pos2++;
239 }
240 } else {
241 min2i = pos2;
242 pos2++;
243 }
244 count[vocab_size + a] = count[min1i] + count[min2i];
245 parent_node[min1i] = vocab_size + a;
246 parent_node[min2i] = vocab_size + a;
247 binary[min2i] = 1;
248 }
249 // Now assign binary code to each vocabulary word
250 for (a = 0; a < vocab_size; a++) {
251 b = a;
252 i = 0;
253 while (1) {
254 code[i] = binary[b];
255 point[i] = b;
256 i++;
257 b = parent_node[b];
258 if (b == vocab_size * 2 - 2) break;
259 }
259 }
260 vocab[a].codelen = i;
261 vocab[a].point[0] = vocab_size - 2;
262 for (b = 0; b < i; b++) {
263 vocab[a].code[i - b - 1] = code[b];
264 vocab[a].point[i - b] = point[b] - vocab_size;
265 }
266 }
267 free(count);
268 free(binary);
269 free(parent_node);
270 }
因为此前vocab vector已经排过序了，所以每次取最小的两个子树根节点做为一个新增父节点的子节点，以此地推，则时间复杂度为
O(time) = vocab_size/2 + vocab_size/4 + ... + vocab_size / n
= vocab_size
大致思想如下：
由底向上一层层构建Huffman树，可以跟着代码走一走，很好理解。
神经网络的参数存储，包括HS和NEG。
350 void InitNet() {
351 long long a, b;
352 unsigned long long next_random = 1;
353 a = posix_memalign((void **)&syn0, 128, (long long)vocab_size * layer1_size * sizeof(real));
354 if (syn0 == NULL) {printf("Memory allocation failed\n"); exit(1);}
355 if (hs) {
356 a = posix_memalign((void **)&syn1, 128, (long long)vocab_size * layer1_size * sizeof(real));
357 if (syn1 == NULL) {printf("Memory allocation failed\n"); exit(1);}
358 for (a = 0; a < vocab_size; a++) for (b = 0; b < layer1_size; b++)
359 syn1[a * layer1_size + b] = 0;
360 }
361 if (negative>0) {
362 a = posix_memalign((void **)&syn1neg, 128, (long long)vocab_size * layer1_size * sizeof(real));
363 if (syn1neg == NULL) {printf("Memory allocation failed\n"); exit(1);}
364 for (a = 0; a < vocab_size; a++) for (b = 0; b < layer1_size; b++)
365 syn1neg[a * layer1_size + b] = 0;
366 }
367 for (a = 0; a < vocab_size; a++) for (b = 0; b < layer1_size; b++) {
368 next_random = next_random * (unsigned long long)25214903917 + 11;
369 syn0[a * layer1_size + b] = (((next_random & 0xFFFF) / (real)65536) - 0.5) / layer1_size;
370 }
371 CreateBinaryTree();
372 }
预计算Sigmoid函数值表，作用就是加速计算。
708 expTable = (real *)malloc((EXP_TABLE_SIZE + 1) * sizeof(real));
709 for (i = 0; i < EXP_TABLE_SIZE; i++) {
710 expTable[i] = exp((i / (real)EXP_TABLE_SIZE * 2 - 1) * MAX_EXP); // Precompute the exp() table
711 expTable[i] = expTable[i] / (expTable[i] + 1); // Precompute f(x) = x / (x + 1)
712 }
对于单个词的参数更新，这一块我也没理太清晰，就不纠结了，感兴趣可以自己看源码。
496 for (a = b; a < window * 2 + 1 - b; a++) if (a != window) {
497 c = sentence_position - window + a;
498 if (c < 0) continue;
499 if (c >= sentence_length) continue;
500 last_word = sen[c];
501 if (last_word == -1) continue;
502 l1 = last_word * layer1_size;
503 for (c = 0; c < layer1_size; c++) neu1e[c] = 0;
504 // HIERARCHICAL SOFTMAX
505 if (hs) for (d = 0; d < vocab[word].codelen; d++) {
506 f = 0;
507 l2 = vocab[word].point[d] * layer1_size;
508 // Propagate hidden -> output
509 for (c = 0; c < layer1_size; c++) f += syn0[c + l1] * syn1[c + l2];
510 if (f <= -MAX_EXP) continue;
511 else if (f >= MAX_EXP) continue;
512 else f = expTable[(int)((f + MAX_EXP) * (EXP_TABLE_SIZE / MAX_EXP / 2))];
513 // 'g' is the gradient multiplied by the learning rate
514 g = (1 - vocab[word].code[d] - f) * alpha;
515 // Propagate errors output -> hidden
516 for (c = 0; c < layer1_size; c++) neu1e[c] += g * syn1[c + l2];
517 // Learn weights hidden -> output
518 for (c = 0; c < layer1_size; c++) syn1[c + l2] += g * syn0[c + l1];
519 }
520 // NEGATIVE SAMPLING
521 if (negative > 0) for (d = 0; d < negative + 1; d++) {
522 if (d == 0) {
523 target = word;
524 label = 1;
525 } else {
526 next_random = next_random * (unsigned long long)25214903917 + 11;
527 target = table[(next_random >> 16) % table_size];
528 if (target == 0) target = next_random % (vocab_size - 1) + 1;
529 if (target == word) continue;
530 label = 0;
531 }
532 l2 = target * layer1_size;
533 f = 0;
534 for (c = 0; c < layer1_size; c++) f += syn0[c + l1] * syn1neg[c + l2];
535 if (f > MAX_EXP) g = (label - 1) * alpha;
536 else if (f < -MAX_EXP) g = (label - 0) * alpha;
537 else g = (label - expTable[(int)((f + MAX_EXP) * (EXP_TABLE_SIZE / MAX_EXP / 2))]) * alpha;
538 for (c = 0; c < layer1_size; c++) neu1e[c] += g * syn1neg[c + l2];
539 for (c = 0; c < layer1_size; c++) syn1neg[c + l2] += g * syn0[c + l1];
540 }
541 // Learn weights input -> hidden
542 for (c = 0; c < layer1_size; c++) syn0[c + l1] += neu1e[c];
543 }
总的来说，word2vec的实现给人的感觉非常优雅，嗯，优雅。
- word2vec源码
- word2vec Google项目
relate reading
- Galina Olejnik, Word embeddings: exploration, explanation, and exploitation
- Galina Olejnik, Hierarchical softmax and negative sampling: short notes worth telling
wordembedding in fasttext
只记录与word2vec有明显差异的地方。
fasttext原理
fasttext是一个词预测一个词，即演变成一个二分类问题。
Subword Model，其思想就是考虑到词的形态学，很多语言都会有prefix，stem，suffix，fasttext将character-ngram当作一个可调整的参数，不同语言的prefix，suffix的长度会有差异。这么做对于稀有词的表示是有益的，因为数据预处理过程中会去调一些稀有词，对于没有出现在语料里的词也是可以做表示的。其实对于象形文字中文来说，这个思想有更好的适用性，例如魑魅魍魉 饕餮 圆圈在表意上就很相近。
去character-ngram为3，对于where,表示为
whe her ere re>
分值计算变为所有character-ngram的和：
因为fasttext引入了Subword Model的概念，所以对于输入层计算次数变为了(V+B)xD，其中V为词量，B为subword的存储空间大小，D为wordembedding维数，所以fasttext相比word2vec，word/thread/second值会稍低一点。
fasttext实现
fasttext存储word，也是用的HashTable，大致结构与word2vec相同。
其实对于where，默认minn是3，maxnn是6，对于其实际存储的character-ngram为
whe wher where where> her here here> ere ere> re>
这样能更好是适用于prefix，stem，suffix长度的变化，也能很好的保留词的原意。
172 void Dictionary::computeSubwords(
173 const std::string& word,
174 std::vector& ngrams,
175 std::vector* substrings) const {
176 for (size_t i = 0; i < word.size(); i++) {
177 std::string ngram;
178 if ((word[i] & 0xC0) == 0x80) {
179 continue;
180 }
181 for (size_t j = i, n = 1; j < word.size() && n <= args_->maxn; n++) {
182 ngram.push_back(word[j++]);
183 while (j < word.size() && (word[j] & 0xC0) == 0x80) {
184 ngram.push_back(word[j++]);
185 }
186 if (n >= args_->minn && !(n == 1 && (i == 0 || j == word.size()))) {
187 int32_t h = hash(ngram) % args_->bucket;
188 pushHash(ngrams, h);
189 if (substrings) {
190 substrings->push_back(ngram);
191 }
192 }
193 }
194 }
195 }
对于word2vec，Skipgram采用的是随机窗口位置，即input word可以在窗口内的固定位置，fasttext输入词总是在中心位置，个人更喜欢word2vec的处理方式。
训练过程也都大同小异，不过，fasttext的代码更像是一个ML的简易框架，word2vec由于是c写的，很难扩展，也很难维护。
text classification in fasttext
这个看了源码和论文就顺带记录吧。
fasttext linear model:
代码和CBOW实现差不多，只不过output变成了__label__，对于实际应用的话loss采用OneVsAll比较好，对于多label而言，可能每一个label的置信度都很低，这样可以不出结果，而且后处理策略也比较好做控制。对于每个label数据量不够不均衡的情况，也可以用这个思想去做样本均衡。
TreeHole
期望以后能看更多的论文，做更多的实现，不限于工作相关领域，能把其他领域所了解的有趣的东西，值得记录下来的东西，抽时间记录在这里。
references
- fasttext site
- P. Bojanowski*, E. Grave*, A. Joulin, T. Mikolov, Enriching Word Vectors with Subword Information
- Tomas Mikolov, Kai Chen, Greg Corrado, Jeffrey Dean, Efficient Estimation of Word Representations in Vector Space
- Tomas Mikolov, Ilya Sutskever, Kai Chen, Greg Corrado, Jeffrey Dean, Distributed Representations of Words and Phrases and their Compositionality
- Tomas Mikolov, Wen-tau Yih, Geoffrey Zweig, Linguistic Regularities in Continuous Space Word Representations
- Armand Joulin, Edouard Grave, Piotr Bojanowski, Tomas Mikolov, Bag-of-Tricks-for-Efficient-Text-Classification