华为杯数学建模比赛经验分享第二期——编程手篇
数学建模比赛中编程手是较为重要的角色,不仅需要根据建模手的思路完成代码的编写,还需要与写作手沟通结果分析与呈现。 所以,编程手必须在不同的阶段完成相应的学习,这里我把它分为赛前和赛中。
1、赛前
在短短4天的学习新的代码并运用起来这对于大多数人来说是困难的,所以需要编程手在赛前多去实战一些代码,包括:预测类、评价类、优化类、机理模型类等。 只有平时积累的多,比赛时才能更快的完成编程任务。 这是对编程手赛前准备的基本要求。
对于预测类的问题,不仅仅是预测模型(BP、SVM、LSTM等)的使用,重要的是对原始数据的预处理,数学建模比赛中给的数据,往往会存在异常值、缺失值等,所以建模手对应就应该在赛前学习或者了解一些异常值剔除的方法代码实现、补齐缺失值的代码,对应的方法我不在这里赘述,大家可以去百度搜索数据清洗的方法。 对于优化类,那就要更加准备一些常用的优化求解器CPLEX、gurobi等,这里要做到能熟悉其编程规则。 对于机理类,以前的赛题中会有传染病模型一类的,我们可以参照这一类模型的思路对类似的问题进行数学建模等。 综上,对建模手来说,要想在数学建模比赛中获奖那就是不断的积累。
2、赛中
比赛中编程手需要根据建模手的思路完成代码的编写,有些时候由于时间问题或者个人编程能力有限,无法完成建模手建立模型的编写。 这时候就需要与建模手进行沟通将模型进行简化,进而完成编程。 其次,编程手也需要把代码的最终数据和初步的实验结果图交给写作手进一步加工。 如果比赛中有充分的时间,我建议编程手可以多用一些方法,举个例子说,在预测类模型中,我们最终选用的模型可能是LSTM,那我们就可以用BP、SVM等一些常规模型作为比较,这也是一个加分项。 值得注意的是,使用了方法对比,那就要在论文中对各类方法的结果进行分析,即告诉评审专家我使用的方法为什么好的问题? 这种问题的回答往往可以在模型的原理介绍中进行描诉,最后在结果分析那一块体现一下即可。 同样地,要在题目分析之后的技术流程图中体现你的方法对比,这样会让你的整个思路更清晰,实验结果更可信。
这里举一个例子:以ECG信号的分类为例。 采用1DCNN和支持向量机进行效果对比。 对应的部分代码如下:
%%1DCNNclear;clc;%% 载入数据;fprintf('Loading data...\n');tic;load('N_dat.mat');load('L_dat.mat');load('R_dat.mat');load('V_dat.mat');fprintf('Finished!\n');toc;fprintf('=============================================================\n');%% 控制使用数据量,每一类5000,并生成标签,one-hot编码;fprintf('Data preprocessing...\n');tic;Nb=Nb(1:5000,:);Label1=repmat([1;0;0;0],1,5000);Vb=Vb(1:5000,:);Label2=repmat([0;1;0;0],1,5000);Rb=Rb(1:5000,:);Label3=repmat([0;0;1;0],1,5000);Lb=Lb(1:5000,:);Label4=repmat([0;0;0;1],1,5000);Data=[Nb;Vb;Rb;Lb];Label=[Label1,Label2,Label3,Label4];clear Nb;clear Label1;clear Rb;clear Label2;clear Lb;clear Label3;clear Vb;clear Label4;Data=Data-repmat(mean(Data,2),1,250); %使信号的均值为0,去掉基线的影响;fprintf('Finished!\n');toc;fprintf('=============================================================\n');%% 数据划分与模型训练测试;fprintf('Model training and testing...\n');Nums=randperm(20000); %随机打乱样本顺序,达到随机选择训练测试样本的目的;train_x=Data(Nums(1:10000),:);test_x=Data(Nums(10001:end),:);train_y=Label(:,Nums(1:10000));test_y=Label(:,Nums(10001:end));train_x=train_x';test_x=test_x';cnn.layers = {struct('type', 'i') %input layerstruct('type', 'c', 'outputmaps', 4, 'kernelsize', 31,'actv','relu') %convolution layerstruct('type', 's', 'scale', 5,'pool','mean') %sub sampling layerstruct('type', 'c', 'outputmaps', 8, 'kernelsize', 6,'actv','relu') %convolution layerstruct('type', 's', 'scale', 3,'pool','mean') %subsampling layer};cnn.output = 'softmax'; %确定cnn结构;%确定超参数;opts.alpha = 0.01; %学习率;opts.batchsize = 16; %batch块大小;opts.numepochs = 30; %迭代epoch;cnn = cnnsetup1d(cnn, train_x, train_y); %建立1D CNN;cnn = cnntrain1d(cnn, train_x, train_y,opts); %训练1D CNN;[er,bad,out] = cnntest1d(cnn, test_x, test_y);%测试1D CNN;[~,ptest]=max(out,[],1);[~,test_yt]=max(test_y,[],1);Correct_Predict=zeros(1,4); %统计各类准确率;Class_Num=zeros(1,4); %并得到混淆矩阵;Conf_Mat=zeros(4);for i=1:10000Class_Num(test_yt(i))=Class_Num(test_yt(i))+1;Conf_Mat(test_yt(i),ptest(i))=Conf_Mat(test_yt(i),ptest(i))+1;if ptest(i)==test_yt(i)Correct_Predict(test_yt(i))= Correct_Predict(test_yt(i))+1;endendACCs=Correct_Predict./Class_Num;fprintf('Accuracy = %.2f%%\n',(1-er)*100);fprintf('Accuracy_N = %.2f%%\n',ACCs(1)*100);fprintf('Accuracy_V = %.2f%%\n',ACCs(2)*100);fprintf('Accuracy_R = %.2f%%\n',ACCs(3)*100);fprintf('Accuracy_L = %.2f%%\n',ACCs(4)*100);figure(1)confusionchart(test_y,ptest)
%%支持向量机clear;clc;%% 载入数据;fprintf('Loading data...\n');tic;load('N_dat.mat');load('L_dat.mat');load('R_dat.mat');load('V_dat.mat');fprintf('Finished!\n');toc;fprintf('=============================================================\n');%% 控制使用数据量,每一类5000,并生成标签;fprintf('Data preprocessing...\n');tic;Nb=Nb(1:5000,:);Label1=ones(1,5000);%Label1=repmat([1;0;0;0],1,5000);Vb=Vb(1:5000,:);Label2=ones(1,5000)*2;%Label2=repmat([0;1;0;0],1,5000);Rb=Rb(1:5000,:);Label3=ones(1,5000)*3;%Label3=repmat([0;0;1;0],1,5000);Lb=Lb(1:5000,:);Label4=ones(1,5000)*4;%Label4=repmat([0;0;0;1],1,5000);Data=[Nb;Vb;Rb;Lb];Label=[Label1,Label2,Label3,Label4];Label=Label';clear Nb;clear Label1;clear Rb;clear Label2;clear Lb;clear Label3;clear Vb;clear Label4;Data=Data-repmat(mean(Data,2),1,250); %使信号的均值为0,去掉基线的影响;fprintf('Finished!\n');toc;fprintf('=============================================================\n');%% 利用小波变换提取系数特征,并切分训练和测试集;fprintf('Feature extracting and normalizing...\n');tic;Feature=[];for i=1:size(Data,1)[C,L]=wavedec(Data(i,:),5,'db6'); %% db6小波5级分解;endNums=randperm(20000); %随机打乱样本顺序,达到随机选择训练测试样本的目的;train_x=Feature(Nums(1:10000),:);test_x=Feature(Nums(10001:end),:);train_y=Label(Nums(1:10000));test_y=Label(Nums(10001:end));[train_x,ps]=mapminmax(train_x',0,1); %利用mapminmax内建函数特征归一化到0,1之间;test_x=mapminmax('apply',test_x',ps);train_x=train_x';test_x=test_x';fprintf('Finished!\n');toc;fprintf('=============================================================\n');%% 训练SVM,并测试效果;fprintf('SVM training and testing...\n');tic;model=libsvmtrain(train_y,train_x,'-c 2 -g 1'); %模型训练;[ptest,~,~]=libsvmpredict(test_y,test_x,model); %模型预测;Correct_Predict=zeros(1,4); %统计各类准确率;Class_Num=zeros(1,4);Conf_Mat=zeros(4);for i=1:10000Class_Num(test_y(i))=Class_Num(test_y(i))+1;Conf_Mat(test_y(i),ptest(i))=Conf_Mat(test_y(i),ptest(i))+1;if ptest(i)==test_y(i)Correct_Predict(test_y(i))= Correct_Predict(test_y(i))+1;endendACCs=Correct_Predict./Class_Num;fprintf('Accuracy_N = %.2f%%\n',ACCs(1)*100);fprintf('Accuracy_V = %.2f%%\n',ACCs(2)*100);fprintf('Accuracy_R = %.2f%%\n',ACCs(3)*100);fprintf('Accuracy_L = %.2f%%\n',ACCs(4)*100);toc;figure(1)confusionchart(test_y,ptest)
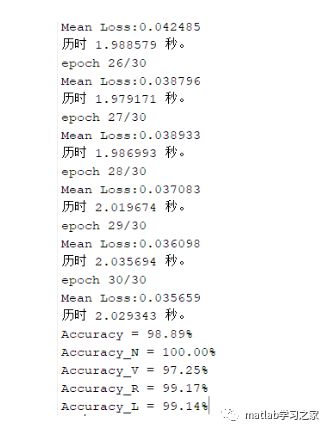
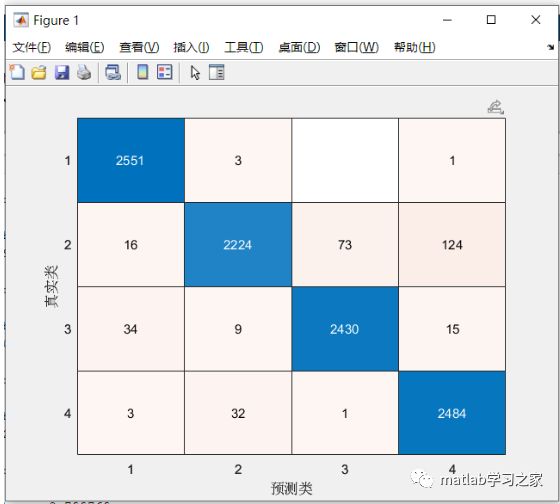
结果对比:
1DCNN结果:
SVM结果:
通过两个模型的结果对比可知,1DCNN明显优于SVM。为什么1DCNN明显优于SVM,那我们可以从算法原理的角度去剖析,这里不做详述。