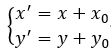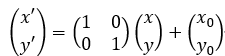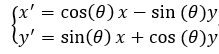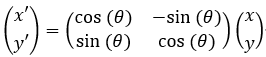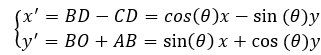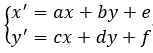二维平面坐标系转换

二维平面坐标系转换

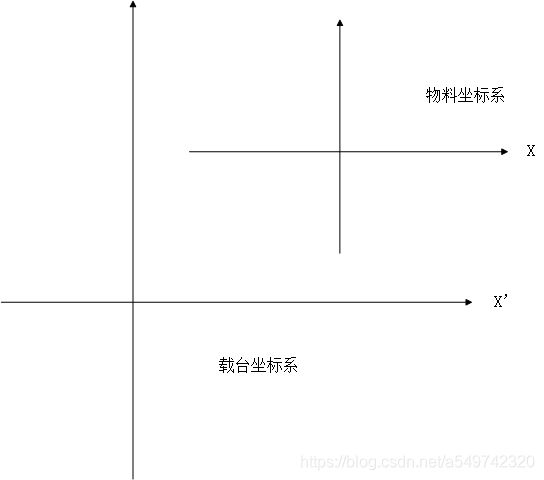
在运动控制中，常涉及到物料坐标系与载台坐标系之间的转换。
通常用坐标转换矩阵实现同一点在不同坐标系的转换，即指将两个点之间的仿射关系以转换矩阵的形式表现出来，转换矩阵作用于原始点的坐标，得到相对应的通过（平移，缩放，旋转）得到的新的点的坐标。

平移：

点P(x,y)平移得到点P'(x',y'),

矩阵表示：

缩放：

矩阵表示：

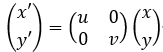
旋转：

矩阵表示：

旋转证明：

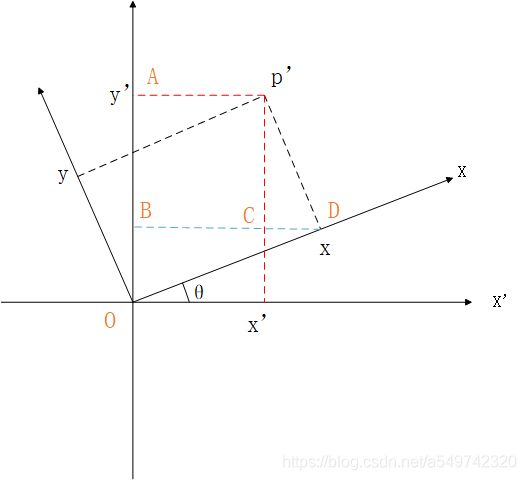
点P向逆时针旋转了θ度，坐标系如下图，

依图可知，

其中的旋转角度θ求法：已知对应坐标系下的两点坐标，求两向量的夹角，两向量的夹角的cos值等于两向量的数量积除以两向量的模的乘积

假设，已知物料坐标系中两点坐标p1(x1,y1),p2(x2,y2),其两点在载台坐标系中的坐标为p3(x3,y3),p4(x4,y4),那么

坐标转换矩阵

如果一个点同时进行了平移，缩放，旋转，用以下坐标变换矩阵：

即就是a,b,c,d为缩放、旋转的系数，e,f为平移量

eg:
物料坐标系与载台坐标系如下：

先旋转物料坐标系180°，使其与载台坐标系一致：

C#实现坐标转换矩阵：

using MathNet.Numerics.LinearAlgebra;
using MathNet.Numerics.LinearAlgebra.Double;
class CoorTransform
    {
        public CoorTransform() { }

        public double Mark1_cust_position_x { get; set; }
        public double Mark1_cust_position_y { get; set; }
        public double Mark2_cust_position_x { get; set; }
        public double Mark2_cust_position_y { get; set; }
        public double Mark1_stage_position_x { get; set; }
        public double Mark1_stage_position_y { get; set; }
        public double Mark2_stage_position_x { get; set; }
        public double Mark2_stage_position_y { get; set; }
        Matrix matrix_rotation { get; set; }   //转换矩阵

        // 设置转换矩阵矩阵   如不同坐标系应先完成坐标系转换（这里的不同指左手坐标系和右手坐标系）
        public void SetMatrix()
        {
            double s1_x = Mark2_cust_position_x - Mark1_cust_position_x;
            double s1_y = Mark2_cust_position_y - Mark1_cust_position_y;

            double s2_x = Mark2_stage_position_x - Mark1_stage_position_x;
            double s2_y = Mark2_stage_position_y - Mark1_stage_position_y;



            double k = 1;

            var vectorA = new DenseVector(new[] { s1_x, s1_y });

            var vectorB = new DenseVector(new[] { s2_x, s2_y });


            double d = vectorA * vectorB;
            //两向量的夹角的cos值=向量的数量积/向量模的乘积    向量的夹角即为两坐标系间的旋转角度
            var cos_sg = (vectorA * vectorB) / (Math.Sqrt(s1_x * s1_x + s1_y * s1_y) * System.Math.Sqrt(s2_x * s2_x + s2_y * s2_y));

            var sin_sg = Math.Sin(Math.Acos(cos_sg));

            //缩放比例
            k = Math.Sqrt((s2_x * s2_x + s2_y * s2_y) / (s1_x * s1_x + s1_y * s1_y));

            if (((s1_y / s1_x) > (s2_y / s2_x)) & (s1_x > 0))
            {
                sin_sg = -sin_sg;
            }


            double[,] stage2 =
           {

                { k*cos_sg, k*-sin_sg},
                { k*sin_sg,k*cos_sg},
            };

            matrix_rotation = DenseMatrix.OfArray(stage2);

            //两坐标系间的偏移
            double offset_x = Mark1_stage_position_x - Mark1_cust_position_x;
            double offset_y = Mark1_stage_position_y - Mark1_cust_position_y;


            double[,] stage1 =
            {
                { k*cos_sg, k*-sin_sg,offset_x},
                { k*sin_sg,k*cos_sg,offset_y},
                { 0,0,1}
            };

            matrix_rotation = DenseMatrix.OfArray(stage1);
        }

        public void Check(double x1, double y1, double x2, double y2, double x3, double y3, double x4, double y4,double x5, double y5)
        {
            Mark1_cust_position_x = x1;
            Mark1_cust_position_y = y1;
            Mark2_cust_position_x = x2;
            Mark2_cust_position_y = y2;
            Mark1_stage_position_x = x3;
            Mark1_stage_position_y = y3;
            Mark2_stage_position_x = x4;
            Mark2_stage_position_y = y4;

            SetMatrix();
            //由于物料坐标系做了旋转变换(180°)，故此坐标点均乘以-1，即旋转矩阵（-1  0
            //                                                           0  -1)
            var vectorsssss = new DenseVector(new[] { -x5, -y5, 1 });
            var result = matrix_rotation * vectorsssss;
        }
    }

 

 

参考：https://blog.csdn.net/Xu_Claire/article/details/101477540