算法合集：二分——pdd每次都能砍一半吗？

二分以其优秀的时间复杂度而出名，借助二分的思想可以实现很多解题方法，像二分答案、三分都是基于二分。另外线段树也是基于二分，分治思想更是与二分不可分割。
注：本文非题解，而是二分精讲
文末有二分（lower_bound、upper_bound）、三分的模板

一、二分查找

先介绍一下lower_bound和upper_bound

lower_bound：第一个 >= target的数，没找到返回数组长度
upper_bound：最后一个 <= target的数，没找到返回-1

借助lower_bound和upper_bound，使得二分的应用更加灵活，不只是局限于返回特定的target
1、题目一：LeetCode 34 在排序数组中查找元素的第一个和最后一个位置
这题若基于普通二分就有些费脑子，因为target不一定在数组中。另外若挨个遍历，复杂度就到O(N)了。
利用lower_bound和upper_bound可以既达到O(logN)的复杂度，又不需要特别在意target是否在数组中。

target在数组中的case：
输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]

第一个 >= target的数也就是index = 3位置的8，最后一个 <= target的数也就是index = 4位置的8

target不在数组中的case
输入：nums = [5,7,7,8,8,10], target = 6
输出：[-1,-1]

第一个 >= target的数也就是index = 1位置的7，最后一个 <= target的数也就是index = 0位置的5
由于找到的5和7均不为target，此时返回-1即可。
于是利用lower_bound和upper_bound完成算法

public int[] searchRange(int[] nums, int target) {
    // 找第一个<=target和第一个>=target的数
    if (nums.length == 0)
        return new int[] {-1, -1};
    int[] ans = new int[2];
    // lower_bound，第一个>=
    int l = 0, r = nums.length;
    while (l < r) {
        int mid = (l + r) >> 1;
        if (nums[mid] >= target)
            r = mid;
        else
            l = mid + 1; 
    }
    ans[0] = r;
    // upper_bound，最后一个<=
    l = -1;
    r = nums.length - 1;
    while (l < r) {
        int mid = (l + r + 1) >> 1;
        if (nums[mid] <= target)
            l = mid;
        else
            r = mid - 1;
    }
    ans[1] = r;
    // 判断target是否在数组中
    if (ans[0] > ans[1]) {
        ans[0] = -1;
        ans[1] = -1;
    }
    return ans;
}

2、题目二：LeetCode 69 x的平方根
题目不允许使用内置函数，且只保留整数部分，那么暴力算法便是

// 伪代码
for (int i from 1 to x)
	if (i * i > target)
		return i - 1;

若利用二分的想法，想到upper_bound，寻找最后一个i * i <= target的数
注意一下越界即可

public int mySqrt(int x) {
    // 找最大的ans，使得ans ^ 2 <= x
    long l = 0, r = (long)x;
    while (l < r) {
        long mid = (l + r + 1) >> 1;
        if (mid * mid <= x)
            l = mid;
        else
            r = mid - 1;
    }
    return (int)r;
}

3、题目三：LeetCode 153 寻找排序数组中的最小值
对于非严格递增的数组，二分查找一样有效，只要明确跟谁比？比完之后往哪边转移？
对于这道题，无外乎就两种情况：

情况一：left和right处于非递增的区域内：[4,5,6,7,0,1,2]
情况二：left和right处于递增的区域内：[4,5,6,7,0,1,2]
只要算法保证无论向哪边转移，其规律在着两种情况都适用就可以了

若mid = (l + r) /2与l比较
在情况一中，若nums[mid] >= nums[l]，由于最小值一定小于nums[mid]，所以要将l右移才能更精确的将最小值夹在中间，则l取mid右侧l = mid + 1
在情况二中，此时nums[l]是从l到r中最小的，若nums[mid] >= nums[l]时还像情况一一样，l往右移，则会舍弃掉正确答案导致南辕北辙。
所以mid = (l + r) /2得与r比较
在情况一中，若nums[mid] <= nums[r]，此时nums[mid]有可能是答案，所以要将r左移才能更精确的将最小值夹在中间，取r = mid
在情况一中，若nums[mid] <= nums[r]，此时nums[mid]仍然可能是答案，同理取r = mid
其他情况不一一列举了，至于什么时候是>=，什么时候<=，什么时候<或>，分情况怎么讨论？留给读者思考

public int findMin(int[] nums) {
    int l = 0, r = nums.length - 1;
    while (l < r) {
        int mid = (l + r) >> 1;
        if (nums[mid] <= nums[r])
            r = mid;
        else 
            l = mid + 1;
    }
    return nums[l];
}

4、实战题目：
LeetCode 35 搜索插入位置
LeetCode 剑指Offer 53-Ⅱ 0~n-1中缺失的数字
LeetCode 154 寻找排序数组中的最小值Ⅱ
LeetCode 33 搜索旋转排序数组
LeetCode 81 搜索旋转排序数组Ⅱ
LeetCode 4 寻找两个正序数组的中位数

二、三分查找

三分的思想基于二分，但目的与二分不同。三分用以寻找峰值，并且数组必须严格单调，只有一个峰值

对于有极大值的函数f(x)，定义域[l,r]上任意取两点lmid,rmid，使得lmid < rmid
若f(lmid) <= f(rmid)，极值位于[lmid + 1, r]
若f(lmid) > f(rmid)，极值位于[l, rmid - 1]
极小值同理

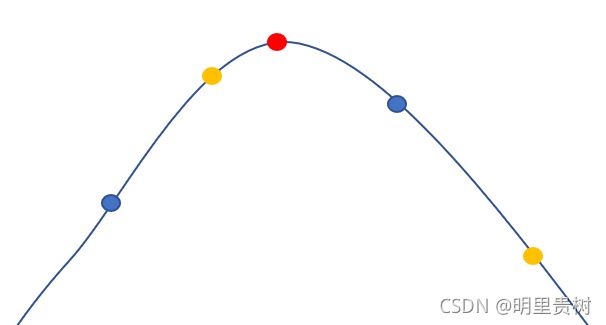
红点代表峰值，其余的点既可以为lmid，也可以是rmid，读者可以自行举例
1、题目一：LeetCode 162 寻找峰值

不止一个峰值时， 三分可以寻找某定义域上任意一个峰值，虽然无法保证此极大值是全局最大值，但三分可以找到其中一个峰值并返回
看懂了上面的图，三分也不需要多言

public int findPeakElement(int[] nums) {
    int l = 0, r = nums.length - 1;
    while (l < r) {
        int lmid = (l + r) / 2;
        int rmid = lmid + 1;
        if (nums[lmid] <= nums[rmid])
            l = lmid + 1;
        else
            r = rmid - 1;
    }
    return l;
}

2、实战题目：
LeetCode 852 山脉数组的顶峰索引

三、二分答案

二分答案的思想源于二分查找，二分答案思想最大的好处在，从直接求答案，变成了利用“夹逼”的方法试出最佳答案

二分答案：
对于一个求最优解的问题，拆分成：枚举一个解 + 判定此解是否正确（正确不一定是最优）
通过遍历解空间 + 判定的方法找到最优解，当解空间具有单调性时，便可以使用二分

1、题目一：LeetCode 410 分割数组的最大值

将长度为n的数组暴力分成m个组，再比较哪个最佳，这个指数级的时间复杂度是我们不愿看到的。
所以我们通过枚举解空间，并以二分的方式来“夹逼”，来找到最优解。

以这个数组为例子：[7,2,5,10,8]，答案为18

1）找到解空间的上下界
找上下界时，不需要思考该解是否正确，只需卡住定义域即可

上界：最大的解，就是不分组，全部数的和
下界：最小的解，也就一个数一个组，为最大的那个数

int l = 0, r = 0; // l是下界，r是上界
for (int i = 0; i < len; i++) {
    l = Math.max(nums[i], l);
    r += nums[i];
}

2）依据二分所需求的单调性，写出判定函数
二分要求的单调性为：函数不严格单调。
同时，对于解空间，随着解的增大，数组中所分的组数也就越少
为了设计出基于解空间不严格单调的判定函数，于是

判定函数：给定一个解T，若m个子数组的各自的和的最大值 <= T，则这个T是正确的

结合下图来理解，如果判定函数这么设计，可以得到下面的非严格单调的解区间

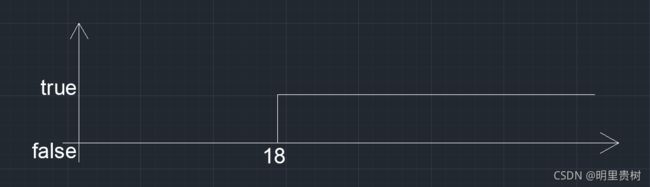
T就是分组时每个组的和的上界，只要这个组的和没超过T，就继续往这个组内添加数。
设当前所分的组的数量为k，题目给定的组数为m
于是依据T进行分组之后，k会随T的增大而减小

• T > 18时，k <= m，我们返回true，告诉程序T大了，为使其减小，我们左移r来减小上界
• T < 18时，k > m，我们返回false，告诉程序T小了，为使其增大，我们右移l来增大上界

利用二分就完成了答案的搜索，判定函数也符合二分特性
3）最终代码实现

思路:
利用二分法猜一个数T
T作为分组依据，sum(nums[i] ~ nums[j]) <= T为一个分组，也就是当前组的和每满T就另起一组
对于T来说存在一个最小值，使得任意大于T的数都能成功分组，直到卡到最小的T为止返回
二分法下界是每个数分一个组，上界是所有数都在同一组

int[] nums;
public int splitArray(int[] nums, int m) {
    this.nums = nums;
    int len = nums.length;
    int l = 0, r = 0; // l是下界，r是上界
    for (int i = 0; i < len; i++) {
        l = Math.max(nums[i], l);
        r += nums[i];
    }
    while (l < r) {
        int mid = (l + r) / 2;
        if (isValid(m, mid, len))
            r = mid;
        else
            l = mid + 1;
    }
    return r;
}

private boolean isValid(int m, int T, int len) {
    int nums_group = 0; // 以T为上界所分的组数
    int cur = 0; // 当前这一组的和
    for (int i = 0; i < len; i++) {
        if (cur + nums[i] <= T) {
            cur += nums[i];
        } else {
            nums_group++;
            i--; // 防止遗漏，当前的nums[i]还未使用
            cur = 0;
        }
    }
    return ++nums_group <= m;
}

2、实战题目：
LeetCode 1482 制作m束花所需要的最少天数
LeetCode 1011 在D天内送达包裹的能力
LeetCode 875 爱吃香蕉的珂珂
LeetCode 911 在线选举

四、二分衍生思想：主动分配，你猜我从哪二分？

说了等于没说系列
有时，二分比较隐晦，但二分的O(logN)的时间复杂度使得二分无论在任意一道（可以用二分解的）题目中成为十分优质的算法，下面的题目中来扒一扒深入的二分 + 分治思想

分配思想：对于求最优解或所有有效解的问题，循环地从某一位置将定义域切开，分治求解

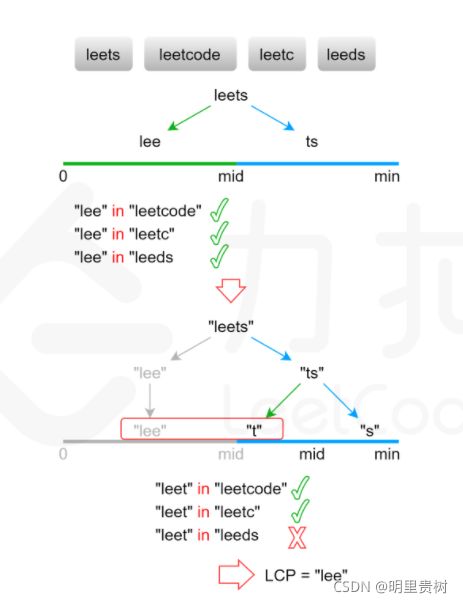
1、题目一：LeetCode 14 最长公共前缀

虽然此题二分的算法不算最优，也不是常见的思路，但种想法值得借鉴
从String[]中找到最短的String，以此为二分的起点

图片来自力扣官方题解：最长公共前缀 官方题解

可以这么去解释，由于最短的String中必然包含答案，便使用二分的方法去一个一个试出答案，有些类似于“二分答案”的思维。若返回true，则给多了；若返回false，则给少了。
2、题目二：LeetCode LCP40 心算挑战
这题的分配便相当明显了
最多拥有cnt张牌，怎么分？i张分给奇数，cnt - i张分给偶数，以此来找到最优解
3、题目三：LeetCode 241 为运算表达式设计优先级
这题也可以用分配的想法去看
在任意位置切一刀，利用分治来解决子问题
具体讲解可以看上期博客：
算法合集：“分治思想”——算法帝国的推恩令

五、二分、三分模板

lower_bound：第一个 >= target的数，没找到返回数组长度

public int lower_bound() {
	int left = 0, right = n;
	while (left < right) {
		int mid = (left + right) >> 1;
		if (array[mid] >= target)
			right = mid;
		else
			left = mid + 1;
		}
	return right;
}

upper_bound：最后一个 <= target的数，没找到返回-1

public int upper_bound() {
	int left = -1, right = n - 1;
	while (left < right) {
		int mid = (left + right + 1) >> 1;
		if (array[mid] <= target)
			left = mid;
		else
			right = mid - 1;
		}
	return right;
}

三分模板

public int findPeak(int[] nums) {
    int left = 0, right = nums.length - 1;
    while (left < right) {
        int lmid = (left + right) / 2;
        int rmid = lmid + 1;
        if (nums[lmid] <= nums[rmid])
            left = lmid + 1;
        else
            right = rmid - 1;
    }
    return left;
}