LeetCode 86 双周赛
文章目录
-
-
- 2395. 和相等的子数组
- 2396. 严格回文的数字
- 2397. 被列覆盖的最多的行数
- 2398. 预算内的最多机器人数目
- 总结
-
2395. 和相等的子数组
题目描述
给你一个下标从 0 开始的整数数组 nums ,判断是否存在 两个 长度为 2 的子数组且它们的 和 相等。注意,这两个子数组起始位置的下标必须 不相同 。
如果这样的子数组存在,请返回 true,否则返回 false 。
子数组 是一个数组中一段连续非空的元素组成的序列。
示例
输入:nums = [4,2,4]
输出:true
解释:元素为 [4,2] 和 [2,4] 的子数组有相同的和 6 。
思路
枚举全部的长度为2的子数组,使用一个集合来判重即可。
class Solution {
public boolean findSubarrays(int[] nums) {
Set<Integer> set = new HashSet<>();
for (int i = 0; i < nums.length - 1; i++) {
int sum = nums[i] + nums[i + 1];
if (set.contains(sum)) return true;
set.add(sum);
}
return false;
}
}
2396. 严格回文的数字
题目描述
如果一个整数 n 在 b 进制下(b 为 2 到 n - 2 之间的所有整数)对应的字符串 全部 都是 回文的 ,那么我们称这个数 n 是 严格回文 的。
给你一个整数 n ,如果 n 是 严格回文 的,请返回 true ,否则返回 false 。
如果一个字符串从前往后读和从后往前读完全相同,那么这个字符串是 回文的 。
- 4 <= n <= 105
示例
输入:n = 9
输出:false
解释:在 2 进制下:9 = 1001 ,是回文的。
在 3 进制下:9 = 100 ,不是回文的。
所以,9 不是严格回文数字,我们返回 false 。
注意在 4, 5, 6 和 7 进制下,n = 9 都不是回文的。
思路
周赛当晚没想到特别好的思路,就直接暴力做了。从n - 2开始循环,是自己心里想的更大的进制,会有更大的可能不是回文,可能会提前返回false,提升一些速度。(实际上后面发现对于所有>=4的数,在n - 2进制下一定不是回文)
class Solution {
public boolean isStrictlyPalindromic(int n) {
int[] arr = new int[20];
for (int i = n - 2; i >= 2; i--) {
int end = 0;
int t = n;
while (t > 0) {
arr[end++] = t % i;
t /= i;
}
int l = 0, r = end - 1;
while (l < r) {
if (arr[l] != arr[r]) return false;
l++;
r--;
}
}
return true;
}
}
实际上,对于任意的正数n,不难推出其在n - 2进制下的表示是12,因为 n = ( n − 2 ) 1 × 1 + ( n − 2 ) 0 × 2 n = (n - 2)^1 × 1 + (n - 2)^0 × 2 n=(n−2)1×1+(n−2)0×2
,特殊的对于n - 2 <= 2的,由于此时n - 2最大是2进制,不会出现12,因为2进制下,每一位最大是1。这种情况特判一下即可,此种情况是n <= 4,对于4,其在2进制下是100,很明显也不是回文。题目的数据范围是[4, 105] ,所以对这个范围内所有的数,在n - 2进制下都不是回文,所以可以直接返回false
class Solution {
public boolean isStrictlyPalindromic(int n) {
return false;
}
}
2397. 被列覆盖的最多的行数
题目描述
给你一个下标从 0 开始的 m x n 二进制矩阵 mat 和一个整数 cols ,表示你需要选出的列数。
如果一行中,所有的 1 都被你选中的列所覆盖,那么我们称这一行 被覆盖 了。
请你返回在选择 cols 列的情况下,被覆盖 的行数 最大 为多少。
m == mat.lengthn == mat[i].length1 <= m, n <= 12mat[i][j]要么是0要么是1。1 <= cols <= n
示例
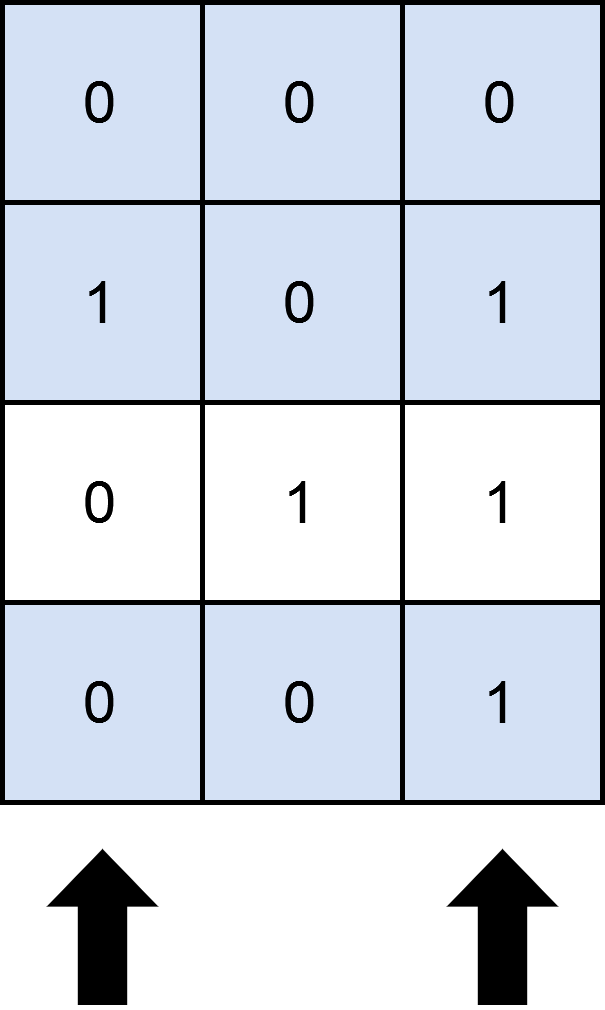
输入:mat = [[0,0,0],[1,0,1],[0,1,1],[0,0,1]], cols = 2
输出:3
解释:
如上图所示,覆盖 3 行的一种可行办法是选择第 0 和第 2 列。
可以看出,不存在大于 3 行被覆盖的方案,所以我们返回 3 。
思路
周赛当晚没有特别好的思路,虽然总有点状态压缩DP和贪心的感觉。在没有思路的情况下,那就只有暴力了。于是尝试使用DFS来枚举所有的方案。
由于是用列去覆盖行,那么我们需要知道每一行都有哪些列是1。也就是,对于每一行,我们需要维护该行的状态。比如上面的示例,第一行的状态是000,第二行的状态是101。
所以先遍历整个矩阵,进行一下预处理,得到每一行的状态(用二进制位表示)。然后先把全0的那些列统计出来。随后使用DFS进行深搜,暴力枚举列的所有选择方案。然后更新答案即可。
class Solution {
int ans = 0;
int n, m;
// 可用的列
boolean[] st;
public int maximumRows(int[][] mat, int cols) {
m = mat.length;
n = mat[0].length;
st = new boolean[n];
List<Integer>[] map = new List[20];
int[] rowState = new int[m]; // 每一行的状态
int numOfAllZeroRow = 0;
for (int i = 0; i < m; i++) {
boolean thisRowAllZero = true;
for (int j = 0; j < n; j++) {
if (mat[i][j] == 1) {
thisRowAllZero = false;
rowState[i] |= 1 << j;
if (map[j] == null) map[j] = new ArrayList<>();
map[j].add(i); // 这一列在第几行出现了
}
}
if (thisRowAllZero) numOfAllZeroRow++;
}
ans = numOfAllZeroRow;
for (int i = 0; i < n; i++) {
st[i] = true;
dfs(i, map, rowState, numOfAllZeroRow, cols);
st[i] = false;
}
return ans;
}
private void dfs(int curCol, List<Integer>[] map, int[] rowState, int coveredRowNum, int remainCols) {
if (remainCols == 0) {
// 无法选择了, 更新答案并退出
ans = Math.max(ans, coveredRowNum);
return ;
}
List<Integer> rowsHasThisCol = map[curCol]; // 包含这一列的那些行
// 对于包含该列的那些行, 更新其状态
int delta = 0; // 该列移除完毕后, 是否有新增的行被完全覆盖
if (rowsHasThisCol != null) {
for (int i : rowsHasThisCol) {
boolean isNotZero = rowState[i] != 0;
rowState[i] -= 1 << curCol;
if (isNotZero && rowState[i] == 0) delta++;
}
}
ans = Math.max(ans, coveredRowNum + delta);
// 深搜下一个列
for (int i = 0; i < n; i++) {
if (st[i]) continue;
st[i] = true;
dfs(i, map, rowState, coveredRowNum + delta, remainCols - 1);
st[i] = false;
}
// 恢复行的状态
if (rowsHasThisCol != null) {
for (int i : rowsHasThisCol) {
rowState[i] |= 1 << curCol;
}
}
}
}
当晚DFS调试了很久,在11点50多终于调试正确后,提交后发现超时
今天重新来看,发现这个思路是没问题的,问题在于,列的组合,是组合问题,而不是排列问题。所以在DFS过程中,会对很多相同的组合进行重复的运算。于是我现在试试加上记忆化,看看能否通过。
-------感觉这个记忆化不是很好加。那我们直接枚举全部的列状态
class Solution {
public int maximumRows(int[][] matrix, int cols) {
int m = matrix.length, n = matrix[0].length;
// 计算行状态
int[] rowState = new int[m];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
rowState[i] |= matrix[i][j] << j;
}
}
int ans = 0;
// 枚举所有列的状态
for (int i = 0; i < 1 << n; i++) {
int cnt = 0;
for (int j = 0; j < n; j++) cnt += i >> j & 1;
// 方案中选中的列的数量不等于cols时, 直接跳过
if (cnt != cols) continue;
// 枚举所有行, 看那些行能够被消除
int t = 0;
for (int j = 0; j < m; j++) {
if ((rowState[j] & i) == rowState[j]) t++;
}
ans = Math.max(ans, t);
}
return ans;
}
}
这道题重点在于位运算,包括使用二进制位来表示行和列的状态,以及通过与运算来判断某一个列状态能否完全消掉一个行状态。
一个数的二进制表示,其实可以映射为一个集合表示。
比如一个行的状态为1001,(最右侧的最低位是第一位)其在第1位,第4位上是1,我们认为是1的位表示为选中,那么二进制数1001就可以表示一个集合{1,4};比如一种列的状态为1101,那么它表示的集合是{1,3,4}。那么{1,4}是{1,3,4}的子集。即1101可以完全覆盖掉1001。所以,用1101和1001做与运算,就相当于用{1,3,4}和{1,4}取交集,那么若A & B = B,说明B是A的子集。
我们也可以用DFS,先把选中列的数量等于cols的所有可能方案预处理出来,保存在一个Set中,然后用这些列状态去进行计算。
位运算的技巧很多,甚至可以出一本书 => 《算法心得:高效算法的奥秘》
上面的代码,是枚举了全部的列状态,枚举了很多不必要的状态。我们能不能只枚举选中k个列的状态呢?是可以id。看下面的Gosper's Hack算法。
扩展:Gosper’s Hack
扩展:对于求解一个n元集合中的k元子集,可以使用Gosper's Hack算法
比如n = 7, k = 4,那么最小的一个二进制数就是0001111,最大的一个二进制数是1111000。
那么我们需要枚举的就是0001111 ~ 1111000 之间全部的1的个数为4的二进制数。
如何快速枚举呢?只要找到当前这个数的下一个数就可以了。下一个数是什么意思?
比如0001111,比这个数大,并且1的个数同样是4的下一个二进制就是0010111,那么0010111的下一个数呢?能够容易的构造出来,是0011011。
所以,我们每次只需要对当前的二进制数,求解其下一个数即可。
观察可以发现,怎么找到一个二进制数的下一个数呢?我们需要以最小的幅度把这个数变大。
而1的个数不能变,很容易想到,想要一个数变大,那么就把二进制位中的1,往左侧与更高位的0进行交换即可。那么如何保证变大的幅度最小呢?那就是在尽可能低的位进行这样的交换。
于是,我们的思路就有了:对于一个二进制数,从右侧最低位往左,找到第一个01,把右侧低位的1,和左侧高位的0进行交换,并把这个01右侧的所有1,全部放到最右侧(最小)。
比如上面的0001111 -> 0010111 -> 0011011
总结来说就是:对一个二进制数
- 从右往左,找到第一个
01,交换这两个位 - 把第一个
01右侧的全部1,全部移动到最右侧
接下来就是如何用位运算来实现这种转换过程。
首先拿出low_bits操作
int low_bits(int n) {
return n & -n;
}
这个操作可以求得一个二进制数的从高位到低位的最后一个1。
比如十进制数x = 114,其二进制表示(假设用8位二进制位,首位是符号位)是01100100,对这个二进制数做low_bits运算得到100。
计算机中的数都是用补码表示的,所以-114对应的二进制数是10011100(取反加一)
两个数做一下与运算,则只有最低位的1被保留了下来。
这个low_bits有啥用呢?可以帮助我们找到第一个01,并交换他们。下面用lb表示low_bits
比如x = 011001110,其lb = 000000010,我们计算x + lb = 011010000。由于lb是最后一个1,那么在原数字的最后一个1的那一位上,加上1,则能够往左进位,进位到遇到第一个0。这样就把第一个01的0所在的那一位变成了1。01左侧部分就完成了。接下来需要求解一下01右侧多少个1,并且要把这些全部1放在最右侧。
由于lb是x中最后一个1,且x + lb后,会一直进位到遇到第一个01。那么第一个01右侧的。就是lb最后一位1所在的位置,到第一个01的0所在的位置,中间的位数。
由于x + lb会从最后一个1,一直进位到第一个0,那么x和x + lb,在最后一个1,和第一个0之间,都是相反数。即最后一个1,到第一个0之间,x对应的二进制位都是1,而x + lb对应的都是0,而其他的位都相同,那么我们可以做一下异或。我们把上面的例子画出来
x = 011001110
lb = 000000010
x + lb = 011010000
x ^ (x + lb) = 000011110
x ^ (x + lb) / lb = 000001111
x ^ (x + lb) / lb >> 2 = 000000011
我们第一个01左侧有2给1,右侧3个1,交换01后,我们先将所有的1移到最右侧,即再除以一个lb,随后少取2给1。
那么,01左侧的部分我们可以通过计算x + lb得到,右侧部分可以通过x ^ (x + lb) / lb >> 2得到,再把左右两部分拼接起来(或运算),即得到下一个数。
这样得到下一个数的时间复杂度是 O ( 1 ) O(1) O(1)的,所以我们通过 C n k C_n^k Cnk 次运算就能得到全部有效的列状态,对于每个列状态,再计算一下所有行,总的复杂度就是 O ( C n k × m ) O(C_n^k × m) O(Cnk×m)
class Solution {
public int maximumRows(int[][] matrix, int cols) {
int m = matrix.length, n = matrix[0].length;
int[] rowState = new int[m];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
rowState[i] |= matrix[i][j] << j;
}
}
int ans = 0;
// 初始状态, 最小值 000011111
// 最大值不能超过 111110000
int x = (1 << cols) - 1;
int limit = 1 << n;
while (x < limit) {
int cnt = 0;
for (int i = 0; i < m; i++) {
if ((rowState[i] & x) == rowState[i]) cnt++;
}
ans = Math.max(ans, cnt);
int lb = x & -x;
int left = x + lb;
int right = ((x ^ left) / lb) >> 2;
x = left | right;
}
return ans;
}
}
2398. 预算内的最多机器人数目
题目描述
你有 n 个机器人,给你两个下标从 0 开始的整数数组 chargeTimes 和 runningCosts ,两者长度都为 n 。第 i 个机器人充电时间为 chargeTimes[i] 单位时间,花费 runningCosts[i] 单位时间运行。再给你一个整数 budget 。
运行 k 个机器人 总开销 是 max(chargeTimes) + k * sum(runningCosts) ,其中 max(chargeTimes) 是这 k 个机器人中最大充电时间,sum(runningCosts) 是这 k 个机器人的运行时间之和。
请你返回在 不超过 budget 的前提下,你 最多 可以 连续 运行的机器人数目为多少。
示例
输入:chargeTimes = [3,6,1,3,4], runningCosts = [2,1,3,4,5], budget = 25
输出:3
解释:
可以在 budget 以内运行所有单个机器人或者连续运行 2 个机器人。
选择前 3 个机器人,可以得到答案最大值 3 。总开销是 max(3,6,1) + 3 * sum(2,1,3) = 6 + 3 * 6 = 24 ,小于 25 。
可以看出无法在 budget 以内连续运行超过 3 个机器人,所以我们返回 3 。
思路
读懂题后,发现这道题并不难。需要求一个最大长度,我们使用二分来做。因为当存在某个长度x满足条件,则答案一定>=x;反之,若x都不满足条件,则答案一定
对于这道题来说,二分的要求解的就是,不超过budget的最大长度,假设这个最大长度为ans,那么对于区间[0, n],所有<= ans,其计算出的开销一定<= budget;所有>ans的部分,其开销一定>budget;我们要求左侧区间的端点。
每次判断当前长度是否能不超过budget。再根据条件往左或往右查找。
随后。对于每个长度,我们用滑动窗口,对chargeTimes使用单调队列来维护当前窗口中的最大值,对runningCosts,预处理成前缀和。
class Solution {
public int maximumRobots(int[] chargeTimes, int[] runningCosts, long budget) {
int n = chargeTimes.length;
int l = 0, r = n;
// 单调队列
int[] q = new int[n];
// 前缀和
long[] preSum = new long[n + 1];
for (int i = 1; i <= n; i++) preSum[i] = preSum[i - 1] + runningCosts[i - 1];
while (l < r) {
int len = l + r + 1 >> 1;
// 在该长度下, 是否能运行且不超过budget
boolean flag = false;
// 队列初始化
int hh = 0, tt = -1;
// 滑动窗口
for (int i = 0, j = 0; i < n; i++) {
// 若当前窗口的左端点已经被移出, 则更新单调队列
while (tt >= hh && q[hh] < j) hh++;
// 单调队列中维护单调递减的元素
while (tt >= hh && chargeTimes[q[tt]] <= chargeTimes[i]) tt--;
q[++tt] = i; // 插入当前位置
if (i - j + 1 == len) {
// 计算一下
int maxCharge = chargeTimes[q[hh]];
long sumRunning = preSum[i + 1] - preSum[j];
if (maxCharge + len * sumRunning <= budget) {
flag = true; // budge 内能够运行len给机器人, 直接break
break;
}
j++;
}
}
// 若当前的长度能够满足预算, 则往右侧查找
if (flag) l = len;
else r = len - 1;
}
return l;
}
}
外层二分长度,复杂度为 O ( l o g n ) O(logn) O(logn),内层每次用滑动窗口(滑动窗口内结合使用了单调队列和前缀和),复杂度 O ( n ) O(n) O(n),总的时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn)
总结
可惜这次周赛没有和第四题打照面。不然有机会A掉第四题的。第三题也是本来有机会过的!这样来看,四舍五入就相当于我AK了,哈哈哈!(YY一下)