浅谈kruskal重构树
食用须知:
*因为临时改动,代码不一定完全正确。
*以下概念来自个人理解,并不十分准确。慎!
Kruskal算法(维护无向图的最小生成森林):每一时刻,从没有选择过的边中选择一条权值最小的且这条边所连接的两个端点不在同一棵树上(不连通),就把该边加上,该边的两个点即为连通。连通情况可以用并查集维护。
Kruskal重构树基于 Kruskal 算法。已知在 Kruskal 的算法中,是按照边权的大小将原图中的边逐一加入到生成森林里,构成最小生成树。而 Kruskal 重构树在原图的 N 个节点的基础上,把 N 个原有节点作为叶子节点。将边权按大小关系,逐一插入到生成森林里。每枚举到一条边,若该边所连接的两个节点不在同一棵树上,那么就增加一个节点,该点的点权即为该边的边权,该点的左孩子和右孩子为该边所连接的两个节点原来所属生成树的根节点(初始根节点都为本身)。这样,就建成了一棵含 2N-1 个节点且所有非叶子节点都有权值的生成树。
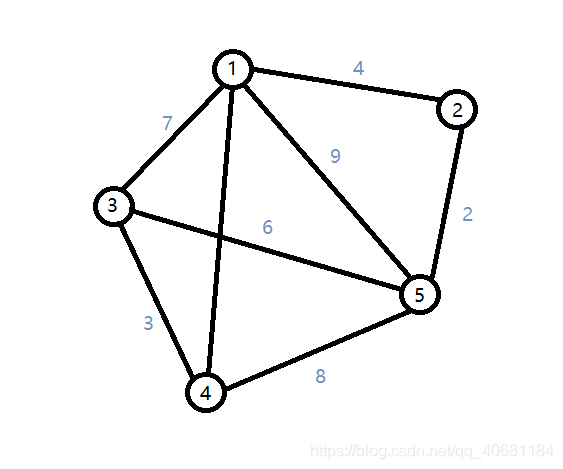
举个栗子:
5个点8条边的一张图:
按时边权从小到大的排序为:
#节点编号 #节点编号 #权值
2 5 2
3 4 3
1 2 4
3 5 6
1 3 7
4 5 8
1 5 9
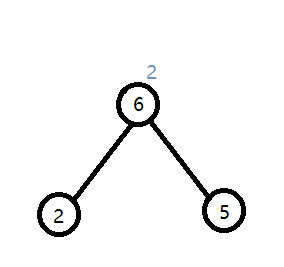
加入第一条边(E[i].u=2,E[i].v=5,E[i].d=2):
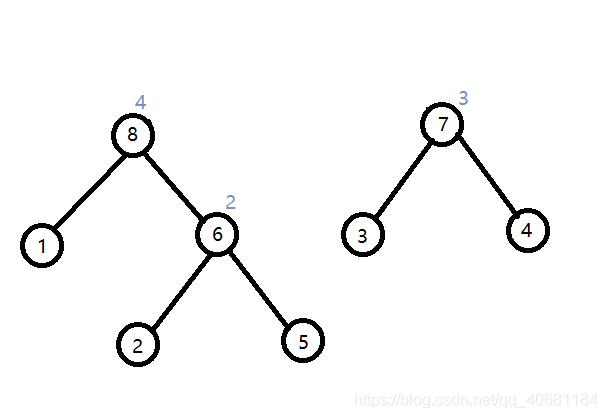
加入第二条边(E[i].u=3,E[i].v=4,E[i].d=3):
加入第三条边(E[i].u=1,E[i].v=2,E[i].d=4):
加入第四条边(E[i].u=3,E[i].v=5,E[i].d=6):
此时,原图中所有的点都集中在一棵生成树中。加入第五~八条边,并不影响原图,不再列出,代码实现如下:
void kruskal(){
for(int i=1;i<=M;i++){
int X=getfa(E[i].u);
int Y=getfa(E[i].v);
if(X==Y) continue;
fa[X]=fa[Y]=++N;//新增节点
pnt[N]=E[i].d;//将边权转移成点权
tr[N].l=E[i].u;
tr[N].r=E[i].v;//记录左右孩子的节点编号
}
}Kruskal 重构树可以实现对于求点 u 到 v 的最大边权的最小值(或最小边权最大)的查询,答案即为在 Kruskal 重构树上,lca(u,v) 的点权。如上图中(上图将边权从小到大排序,解决的是两点之间最大边权的最小值), 点 2 到 点 5 的最大边权的最小值即为点 6 的点权:2 ;点 1 到点 4 的最大边权的最小值即为点 7 的点权:3。根据这个性质,可以完成 BZOJ3742.Network 。
同样,根据如上性质的拓展,我们可以利用倍增解决"从一点出发,规定所经过路径的最大(最小)权值,求能够到达的点"等类似的问题。如上图中,我们想要求得:从 2 出发,经过路径的最大权值为 4 所能够到达哪些点。点 8 的点权为 4,而点 9 的点权为 6。所以,以节点 8 为根节点的子树中的所有叶子节点(2 本身除外),都满足条件要求,用dfs从节点 8 进行搜索,即可求得答案为 1,5 。 具体可以完成 NOI2019T1D1.归程 加深。
<例题>
【BZOJ3732】Network
Description
给你N个点的无向图 (1 <= N <= 15,000),记为:1…N。
图中有M条边 (1 <= M <= 30,000) ,第j条边的长度为: d_j ( 1 < = d_j < = 1,000,000,000).现在有 K个询问 (1 < = K < = 20,000)。
每个询问的格式是:A B,表示询问从A点走到B点的所有路径中,最长的边最小值是多少?Input
第一行: N, M, K。
第2..M+1行: 三个正整数:X, Y, and D (1 <= X <=N; 1 <= Y <= N). 表示X与Y之间有一条长度为D的边。
第M+2..M+K+1行: 每行两个整数A B,表示询问从A点走到B点的所有路径中,最长的边最小值是多少?Output
对每个询问,输出最长的边最小值是多少。
Sample Input
6 6 8
1 2 5
2 3 4
3 4 3
1 4 8
2 5 7
4 6 2
1 2
1 3
1 4
2 3
2 4
5 1
6 2
6 1Sample Output
5
5
5
4
4
7
4
5
kruskal模板。因为求的是"最长的边最小值",将边权从小到大排序。对于每一次询问 A,B ,点 lca(A,B) 的权值即为所求。
代码实现如下:
#include
using namespace std;
int N,M,K,num,lg,fa[30010]={},f[30010][22]={},pnt[30010]={},lin[30010]={},d[30010]={};
struct kk{ int id,next; } e[30010]={};
struct hh{ int x,y; int d; } E[30010]={};
bool mycmp(hh x,hh y){ return x.dd[y]) x^=y^=x^=y;
for(int D=d[y]-d[x],i=0;D;D>>=1,i++)
if(D&1) y=f[y][i];
if(x==y) return x;
for(int i=lg;i>=0;i--)
if(f[x][i]!=f[y][i])
x=f[x][i],y=f[y][i];
return f[x][0];
}//倍增求lca
int main(){
scanf("%d%d%d",&N,&M,&K);
for(int i=1;i<=M;i++) scanf("%d%d%d",&E[i].x,&E[i].y,&E[i].d);
sort(E+1,E+M+1,mycmp);//将边从小到大排序
for(int i=1;i<=N*2;i++) fa[i]=i;//并查集初始化
for(int i=1;i<=M;i++){
int X=getfa(E[i].x);
int Y=getfa(E[i].y);//找到E[i].x,E[i].y所属生成树的根节点
if(X==Y) continue;
fa[X]=fa[Y]=++N;//新增一个节点
pnt[N]=E[i].d;//将边权转移到点上
insert(N,X);
insert(N,Y);//加入新增的点,连接E[i].x和E[i].y原所属生成树的根节点
}
dfs(N);
Red();//倍增求lca预处理
for(int i=1;i<=K;i++){
int A,B;
scanf("%d%d",&A,&B);
printf("%d\n",pnt[lca(A,B)]);
}
return 0;
} 【洛谷P1967】NOIP2013D1T3 货车运输
Description
A国有n座城市,编号从1到n,城市之间有 m 条双向道路。每一条道路对车辆都有重量限制,简称限重。现在有 q 辆货车在运输货物, 司机们想知道每辆车在不超过车辆限重的情况下,最多能运多重的货物。
Input
第一行有两个用一个空格隔开的整数n,m,表示 A 国有 n 座城市和 m 条道路。
接下来 m 行每行3个整数 x, y, z,每两个整数之间用一个空格隔开,表示从 x 号城市到 y 号城市有一条限重为 z 的道路。注意: x 不等于 y,两座城市之间可能有多条道路 。
接下来一行有一个整数 q,表示有 q 辆货车需要运货。
接下来 q 行,每行两个整数 x、y,之间用一个空格隔开,表示一辆货车需要从 x 城市运输货物到 y 城市,注意:x 不等于 y 。
Output
共有 q 行,每行一个整数,表示对于每一辆货车,它的最大载重是多少。如果货车不能到达目的地,输出−1。
Sample Input
4 3
1 2 4
2 3 3
3 1 1
3
1 3
1 4
1 3Sample Output
3
-1
3
方法很多,如:最大生成树+lca,这里不进行详细论述。仅展示 Kruskal 重构树做法。
题目要求"最大载重"。将边权从大到小排序,跟上题基本一样。须注意的是,货车不一定能到大目的地。在输出与进行dfs时,需要进行特判。
代码如下:
#include
using namespace std;
int N,M,K,num,lg,fa[20010]={},f[20010][22]={},pnt[20010]={},lin[20010]={},d[20010]={},vis[20010]={};
struct kk{ int id,next; } e[50010]={};
struct hh{ int x,y; int d; } E[50010]={};
bool mycmp(hh x,hh y){ return x.d>y.d; }
int getfa(int x){ return x==fa[x] ? x : fa[x]=getfa(fa[x]); }
void insert(int x,int y){ e[++num].next=lin[x]; lin[x]=num; e[num].id=y;}
void dfs(int x){
for(int i=lin[x];i;i=e[i].next){
d[e[i].id]=d[x]+1;
f[e[i].id][0]=x;
dfs(e[i].id);
}
}
void Red(){
int n=N;
for(;n;) n/=2,lg++;
for(int i=1;i<=lg;i++)
for(int j=1;j<=N;j++)
f[j][i]=f[f[j][i-1]][i-1];
}
int lca(int x,int y){
if(d[x]>d[y]) x^=y^=x^=y;
for(int D=d[y]-d[x],i=0;D;D>>=1,i++)
if(D&1) y=f[y][i];
if(x==y) return x;
for(int i=lg;i>=0;i--)
if(f[x][i]!=f[y][i])
x=f[x][i],y=f[y][i];
return f[x][0];
}
int main(){
scanf("%d%d",&N,&M);
for(int i=1;i<=M;i++) scanf("%d%d%d",&E[i].x,&E[i].y,&E[i].d);
sort(E+1,E+M+1,mycmp);//从大到小排序
for(int i=1;i<=N*2;i++) fa[i]=i;
for(int i=1;i<=M;i++){
int X=getfa(E[i].x);
int Y=getfa(E[i].y);
if(X==Y) continue;
fa[X]=fa[Y]=++N;
pnt[N]=E[i].d;
insert(N,X);
insert(N,Y);
}
for(int i=N;i>=1;i--)
if(!vis[getfa(i)])
vis[getfa(i)]++,dfs(getfa(i));//如果该生成树没有访问过,进行访问
Red();
scanf("%d",&K);
for(int i=1;i<=K;i++){
int A,B;
scanf("%d%d",&A,&B);
if(fa[A]!=fa[B]) printf("-1\n");//判断是否在同一生成树里
else printf("%d\n",pnt[lca(A,B)]);
}
return 0;
} 【洛谷P4768】NOI D1T1 归程
Description
(题目过长,讲个大意)一张 n 个节点、m 条边的无向连通图,节点的编号从 1 至 n 。每一个节点有两个属性 l,a,l为长度,a 为衡量标准。现有 Q 个询问。给出出发点 v ,和标准 p 。可以先从 v 号点乘车出发,所有乘车经过的路径的 a 值都不能小于p。然后剩下的路径,必须徒步行走。求最少行走路程。
Input
详见洛谷
Output
依次输出各组数据的答案。对于每组数据:
输出 Q 行每行一个整数,依次表示每天的最小步行总路程。
Sample Input1
1
4 3
1 2 50 1
2 3 100 2
3 4 50 1
5 0 2
3 0
2 1
4 1
3 1
3 2Sample Output1
0
50
200
50
150Sample Input2
1
5 5
1 2 1 2
2 3 1 2
4 3 1 2
5 3 1 2
1 5 2 1
4 1 3
5 1
5 2
2 0
4 0Sample Output2
0
2
3
1
dijkatra求出根节点到每一点的最短路。然后将所有的边从大到小排序,建立 kruskal 重构树,同时预处理每一个新增节点子树中的叶子节点到根节点的距离的最小值,通过倍增寻找符合要求的最大子树可以求得答案。(*需要注意数组清空)
#include
using namespace std;
int T,N,M,Q,K,S,Nn,v,p,lg,num,lin[400010]={},f[400010][22]={},fa[400010]={},vis[400010]={},pnt[400010]={};
long long lastans,dis[400010]={},pntt[400010]={};
priority_queue< pair > q;
struct kk{ int next,id; int v; } e[800010]={};
struct hh{ int u,v; int l,a; } E[400010]={};
bool mycmp(hh x,hh y){ return x.a>y.a; }
void insert(int x,int y,int z){ e[++num].next=lin[x]; lin[x]=num; e[num].id=y; e[num].v=z; }
int getfa(int x){ return x==fa[x] ? x : fa[x]=getfa(fa[x]); }
int read(){
char ch; int f=1,num=0;
ch=getchar();
for(;ch<'0'||ch>'9';) {
if(ch=='-') f=-1; ch=getchar();
}
for(;ch>='0'&&ch<='9';){
num=num*10+(ch-'0');
ch=getchar();
}
return num*f;
}
void Clear(int x){
num=0; lastans=0;
memset(lin,0,sizeof(lin));
if(x) return ;
memset(f,0,sizeof(f));
}
void dij(){
memset(dis,30,sizeof(dis));
memset(vis,0,sizeof(vis));
dis[1]=0; q.push(make_pair(0,1));
for(;!q.empty();){
int x=q.top().second; q.pop();
if(vis[x]) continue;
vis[x]++;
for(int i=lin[x];i;i=e[i].next){
if(dis[x]+(long long)e[i].v>=dis[e[i].id]) continue;
dis[e[i].id]=dis[x]+(long long)e[i].v;
q.push(make_pair(-dis[e[i].id],e[i].id));
}
}
}//堆优化的dijkstra
void dfs(int x){
int son=0;
pntt[x]=dis[x];
for(int i=lin[x];i;i=e[i].next){
son++;
f[e[i].id][0]=x;
dfs(e[i].id);
pntt[x]=min(pntt[x],pntt[e[i].id]);//记录该子树中的叶子节点到根节点的最小值
}
}
void Red(){
int n=N; lg=0;
for(;n;) n/=2,lg++;
for(int i=1;i<=lg;i++)
for(int j=1;j<=N;j++)
f[j][i]=f[f[j][i-1]][i-1];
}
int main(){
T=read();
for(;T--;){
Clear(0);//清空
N=read(); M=read(); Nn=N;
for(int i=1;i<=M;i++){
E[i].u=read(); E[i].v=read(); E[i].l=read(); E[i].a=read();
insert(E[i].u,E[i].v,E[i].l);
insert(E[i].v,E[i].u,E[i].l);//建图跑最短路
}
dij();
Clear(1);//清空
sort(E+1,E+M+1,mycmp);//将边权从大到小排序
for(int i=1;i<=N*2;i++) fa[i]=i;//并查集初始化
for(int i=1;i<=M;i++){
int X=getfa(E[i].u);
int Y=getfa(E[i].v);
if(X==Y) continue;
fa[X]=fa[Y]=++N;
pnt[N]=E[i].a;
insert(N,X,0);
insert(N,Y,0);
}//kruskal重构树
dfs(N);
Red();//倍增预处理
Q=read(); K=read(); S=read();
for(int i=1;i<=Q;i++){
int V,P;
V=read(); P=read();
v=(V+(long long)K*lastans-1)%Nn+1;
p=(P+(long long)K*lastans)%(S+1);
for(int j=lg;j>=0;j--)
if(pnt[f[v][j]]>p&&f[v][j]) v=f[v][j];//倍增查找符合要求的最大子树
lastans=pntt[v];
printf("%lld\n",lastans);
}
}
return 0;
}