力扣刷题-数组-滑动窗口法相关题目总结

209. 长度最小的子数组（最小滑窗）

给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度最小的 连续 子数组，并返回其长度。如果不存在符合条件的子数组，返回 0。
示例：
输入：s = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。
注意题目是返回长度即可。

暴力法

class Solution(object):
    def minSubArrayLen(self, target, nums):
        """
        :type target: int
        :type nums: List[int]
        :rtype: int
        """
        ## 难的问题 可以先考虑暴力解法（若没有要求时间复杂度）
        min_len = float('inf') # 先定义一个无穷大 min_len 后续再迭代更新
        for i in range(len(nums)):
            sum = 0
            for j in range(i, len(nums)):
                sum += nums[j]
                if sum >= target:
                    min_len = min(min_len, j-i+1)
                    break # 使用break 防止再遍历下去
        
        return min_len if min_len != float('inf') else 0

时间复杂度：O(n^2)
空间复杂度：O(1)

滑动窗口法

接下来就开始介绍数组操作中另一个重要的方法：滑动窗口。
所谓滑动窗口，就是不断的调节子序列的起始位置和终止位置，从而得出我们要想的结果。
在暴力解法中，是一个for循环滑动窗口的起始位置，一个for循环为滑动窗口的终止位置，用两个for循环 完成了一个不断搜索区间的过程。
那么滑动窗口如何用一个for循环来完成这个操作呢。
首先要思考 如果用一个for循环，那么应该表示 滑动窗口的起始位置，还是终止位置。
如果只用一个for循环来表示 滑动窗口的起始位置，那么如何遍历剩下的终止位置？
此时难免再次陷入 暴力解法的怪圈。
所以 只用一个for循环，那么这个循环的索引，一定是表示 滑动窗口的终止位置。
那么问题来了， 滑动窗口的起始位置如何移动呢？
这里还是以题目中的示例来举例，s=7， 数组是 2，3，1，2，4，3，来看一下查找的过程：

其实从动画中可以发现滑动窗口也可以理解为双指针法的一种！只不过这种解法更像是一个窗口的移动，所以叫做滑动窗口更适合一些。
在本题中实现滑动窗口，主要确定如下三点：

• 窗口内是什么？
• 如何移动窗口的起始位置？
• 如何移动窗口的结束位置？

窗口就是 满足其和 ≥ s 的长度最小的 连续 子数组。
窗口的起始位置如何移动：如果当前窗口的值大于s了，窗口就要向前移动了（也就是该缩小了）。
窗口的结束位置如何移动：窗口的结束位置就是遍历数组的指针，也就是for循环里的索引。
解题的关键在于 窗口的起始位置如何移动，如图所示：

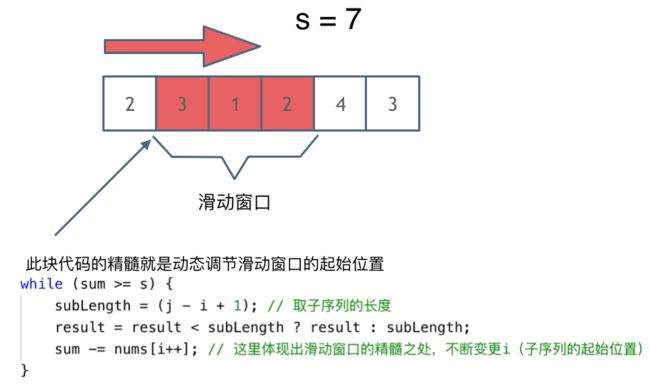
可以发现滑动窗口的精妙之处在于根据当前子序列和大小的情况，不断调节子序列的起始位置。从而将O(n^2)暴力解法降为O(n)。

class Solution(object):
    def minSubArrayLen(self, target, nums):
        """
        :type target: int
        :type nums: List[int]
        :rtype: int
        """
        min_len = float("inf") # 同样也是先初始化一个min_len
        i, sum = 0, 0
        for j in range(len(nums)):
            sum += nums[j]
            while sum >= target:
                min_len = min(min_len, j-i+1)
                sum -= nums[i]
                i += 1 # 这两行是滑动窗口的巧妙之处
        return min_len if min_len != float("inf") else 0

区分时间复杂度：
暴力解题法：O(n^2) 因为第一个for循环在第一个元素的时候，第二个for循环会遍历所有元素；第一个for循环在第二个元素的时候也会遍历在第二个for循环的时候遍历所有元素…）——> n*n=n^2
滑动窗口法：不要以为for里放一个while就以为是O(n^2)啊， 主要是看每一个元素被操作的次数，每个元素在滑动窗后进来操作一次，出去操作一次，每个元素都是被操作两次，所以时间复杂度是 2 × n 也就是O(n)。
子串问题优先滑动窗口。

滑动窗口法模板

一般什么时候会考虑使用 滑动窗口法 ？——>答：当求子串问题（最小长度/最大长度，对应最小滑窗/最大滑窗）时候常常考虑使用滑动窗口法。 若需要种类计数，记得定义一个种类计数器以及种类计数
参考：
作者：HelloPGJC
链接：https://leetcode.cn/problems/fruit-into-baskets/solutions/1437444/shen-du-jie-xi-zhe-dao-ti-he-by-linzeyin-6crr/
来源：力扣（LeetCode）

最小滑窗

最小滑窗模板：给定数组 nums，定义滑窗的左右边界 i, j，求满足某个条件的滑窗的最小长度。

while j < len(nums):
    判断[i, j]是否满足条件（如果是简单的 一般不需要判断条件 如上面的题）
    while 满足条件：
        不断更新结果(注意在while内更新！所谓结果就是求的长度)
        i += 1 （最大程度的压缩i，使得滑窗尽可能的小）
    j += 1

最大滑窗

最大滑窗模板：给定数组 nums，定义滑窗的左右边界 i, j，求满足某个条件的滑窗的最大长度。

while j < len(nums):
    判断[i, j]是否满足条件
    while 不满足条件：
        i += 1 （最保守的压缩i，一旦满足条件了就退出压缩i的过程，使得滑窗尽可能的大）
    不断更新结果（注意在while外更新！）
    j += 1

如上面的题：

class Solution(object):
    def minSubArrayLen(self, target, nums):
        """
        :type target: int
        :type nums: List[int]
        :rtype: int
        """
        min_len = float("inf") # 同样也是先初始化一个min_len
        i, sum = 0, 0
        for j in range(len(nums)):
            sum += nums[j]
            while sum >= target:
                min_len = min(min_len, j-i+1)
                sum -= nums[i]
                i += 1 # 这两行是滑动窗口的巧妙之处
        return min_len if min_len != float("inf") else 0

76. 最小覆盖子串（最小滑窗）

题目难度：困难
给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 “” 。
注意：

• 对于 t 中重复字符，我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
• 如果 s 中存在这样的子串，我们保证它是唯一的答案。

示例 1：
输入：s = “ADOBECODEBANC”, t = “ABC”
输出：“BANC”
解释：最小覆盖子串 “BANC” 包含来自字符串 t 的 ‘A’、‘B’ 和 ‘C’。
示例 2：
输入：s = “a”, t = “a”
输出：“a”
解释：整个字符串 s 是最小覆盖子串。
示例 3:
输入: s = “a”, t = “aa”
输出: “”
解释: t 中两个字符 ‘a’ 均应包含在 s 的子串中，
因此没有符合条件的子字符串，返回空字符串。
求最小子串问题——>滑动窗口法
解析题意：
最小字串——>滑动窗口法
找出的s的子串需要涵盖t中的字符——>会使用字典计数器

class Solution(object):
    def minWindow(self, s, t):
        """
        :type s: str
        :type t: str
        :rtype: str
        """
        i, j = 0, 0
        needMap = defaultdict(int) # 定义一个字典计数器（对字符, 初始化都是0）
        needCnt = len(t) # 最开始 在s中我需要涵盖的字符数就是t中总的字符数
        res = "" # 结果 初始化为 ""
        for c in t:
            needMap[c] += 1 # 为字符计数器赋值
        while j < len(s):
            if s[j] in needMap:
                if needMap[s[j]] > 0:
                     needCnt -= 1 # 有这个字符 那么我需要的字符数就减1
                needMap[s[j]] -= 1 # 因为t中可能有重复字符 所以这个需要减1
            while needCnt == 0:
                if not res or j-i+1 < len(res): # res为空(前面没有结果) 注意是小于len(res) 因为是最小子串
                    res = s[i:j+1] # 获取
                # 上面只是更新了结果 needMap和needCnt还没有更新
                if s[i] in needMap:
                    if needMap[s[i]] == 0:
                        needCnt += 1 # 因为我下一步要移动i 所以如果现在没有这个字符 我需要的字符数加1
                    needMap[s[i]] += 1 # 因为我下一步要移动i 所以如果现在没有这个字符 就要加1 告诉后面我需要
                i += 1 # 更新 i
            j += 1 # 更新j
        return res

904. 水果成篮（最大字串）

你正在探访一家农场，农场从左到右种植了一排果树。这些树用一个整数数组 fruits 表示，其中 fruits[i] 是第 i 棵树的种类 。
你想要尽可能多地收集水果。然而，农场的主人设定了一些严格的规矩，你必须按照要求采摘水果：
你只有 两个 篮子，并且每个篮子只能装 单一类型 的水果。每个篮子能够装的水果总量没有限制。
你可以选择任意一棵树开始采摘，你必须从 每棵 树（包括开始采摘的树）上 恰好摘一个水果 。采摘的水果应当符合篮子中的水果类型。每采摘一次，你将会向右移动到下一棵树，并继续采摘。
一旦你走到某棵树前，但水果不符合篮子的水果类型，那么就必须停止采摘。
给你一个整数数组 fruits ，返回你可以收集的水果的 最大 数目。
解题：
像这种就需要先翻译一下题目意思，就是让你从一个整数数组中，找出其中最长的子数组，然后一个限制条件是，这个最长子数组中的整数最多只能有两种。
本题返回的是子数组长度，不是子数组，注意分清楚
示例 1：
输入：fruits = [1,2,1]
输出：3
解释：可以采摘全部 3 棵树。
示例 2：
输入：fruits = [0,1,2,2]
输出：3
解释：可以采摘 [1,2,2] 这三棵树。
如果从第一棵树开始采摘，则只能采摘 [0,1] 这两棵树。
示例 3：
输入：fruits = [1,2,3,2,2]
输出：4
解释：可以采摘 [2,3,2,2] 这四棵树。
如果从第一棵树开始采摘，则只能采摘 [1,2] 这两棵树。

class Solution(object):
    def totalFruit(self, fruits):
        """
        :type fruits: List[int]
        :rtype: int
        """
        # 初始化
        i, j = 0, 0
        res = 0 # 要求最大 我先初始化为0
        classMap = defaultdict(int) # 因为涉及到种类数 所以需要一个种类计数器
        classCnt = 0 # 因为是求最大 我刚开始计数当然为0

        while j < len(fruits):
            if classMap[fruits[j]] == 0:
                classCnt += 1 # 第一个数 种类肯定是加1
            classMap[fruits[j]] += 1
            while classCnt > 2: # 不符合条件 种类数超过2
                # if classMap[fruits[i]] > 0: # 不能用0判断 因为不知道种类数能不能减1
                if classMap[fruits[i]] == 1:
                    classCnt -= 1 # 因为下一步我就要移动i了, 当前为1 移动一下肯定为0
                classMap[fruits[i]] -= 1 # 该种类数计数也减1
                i += 1
            res = max(res, j-i+1) # 在while外面更新结果
            j += 1
        return res

理解最小滑窗和最大滑窗的更新的不同之处：

因为是符合条件才更新结果，最小滑动窗口中，while的条件是 满足条件 因此在while内更新，而最大滑动窗口中，while的条件是 不满足条件 因此得等到条件满足，也就是退出循环后再更新

1004. 最大连续1的个数 III

给定一个二进制数组 nums 和一个整数 k，如果可以翻转最多 k 个 0 ，则返回 数组中连续 1 的最大个数 。
示例 1：
输入：nums = [1,1,1,0,0,0,1,1,1,1,0], K = 2
输出：6
解释：[1,1,1,0,0,1,1,1,1,1,1]
粗体数字从 0 翻转到 1，最长的子数组长度为 6。
示例 2：
输入：nums = [0,0,1,1,0,0,1,1,1,0,1,1,0,0,0,1,1,1,1], K = 3
输出：10
解释：[0,0,1,1,1,1,1,1,1,1,1,1,0,0,0,1,1,1,1]
粗体数字从 0 翻转到 1，最长的子数组长度为 10。
注意，要理清题意，这里未涉及种类计数，其中 条件 就是 0的数量 因为翻转0是题目已经设定好的。

class Solution(object):
    def longestOnes(self, nums, k):
        """
        :type nums: List[int]
        :type k: int
        :rtype: int
        """
        # 求数组中的子数组 最大个数 ——> 最大滑窗
        # 限制条件是 最大翻转k个0 需要0的个数
        # 想复杂了 还是要理清题意
        i, j = 0, 0
        res = 0
        zeroCnt = 0
        while j < len(nums):
            if nums[j] == 0:
                zeroCnt += 1
            while zeroCnt > k: # 注意是k
                if nums[i] == 0:
                    zeroCnt -= 1 # 因为我下一步要移动i
                i += 1
            res = max(res, j-i+1)
            j += 1
        return res 

3. 无重复字符的最长子串

给定一个字符串 s ，请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:
输入: s = “abcabcbb”
输出: 3
解释: 因为无重复字符的最长子串是 “abc”，所以其长度为 3。
示例 2:
输入: s = “bbbbb”
输出: 1
解释: 因为无重复字符的最长子串是 “b”，所以其长度为 1。
示例 3:
输入: s = “pwwkew”
输出: 3
解释: 因为无重复字符的最长子串是 “wke”，所以其长度为 3。
请注意，你的答案必须是 子串 的长度，“pwke” 是一个子序列，不是子串。

class Solution(object):
    def lengthOfLongestSubstring(self, s):
        """
        :type s: str
        :rtype: int
        """
        # 子串 最大长度 ——> 最大滑窗
        # 不含重复字符 说明遇到字符计数
        # 巧妙之处：将子串中的字符数 与 字典长度联系起来
        # 模板不要用的太死板

        i, j = 0, 0
        res = 0
        char_dict = defaultdict(int)
        while j < len(s):
            char_dict[s[j]] += 1
            while len(char_dict)<j-i+1: # 不满足条件 这个比较难想
                char_dict[s[i]] -= 1 # 下一步就是移动i
                if char_dict[s[i]] == 0:
                    del char_dict[s[i]]
                i += 1
            if len(char_dict) == j - i + 1:  # 巧妙之处
                res = max(res, j-i+1)
            j+=1
        return res

参考：https://programmercarl.com/