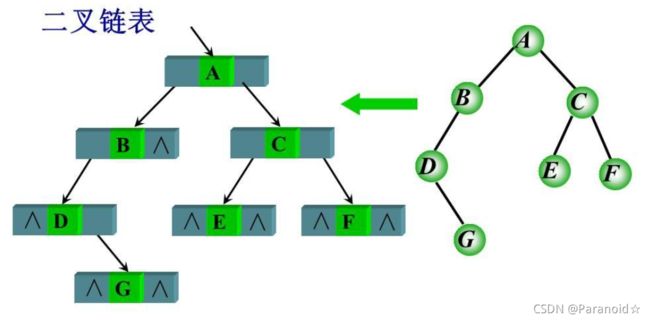
二叉树的遍历(递归算法与非递归算法）

---

前言

习题：
二叉树的前序遍历
二叉树的中序遍历
二叉树的后序遍历

---

提示：以下是本篇文章正文内容

二叉树的递归遍历

二叉树的存储结构一般采用二叉链表

结点结构

struct BiNode
{
	DataType data;
	BiNode *lchild,*rchild;
}

二叉树的基本操作

class BiTree
{
private:
	BiNode *root; //指向根结点的头指针
public:
	BiTree(){root = creat(root);}  //构造函数，建立一棵二叉树
	~BiTree({release(root); //析构函数
	void preOrderO{preOrder(root);} //前序遍历二叉树
	void inOrderO{inOrder(root);} //中序遍历二叉树
	void postOrderO{postOrder(root);}//后序遍历二叉树
	void leverOrderQ; //层序遍历二叉树
private:
	BiNode *creat(BiNode *bt);//构造函数调用
	void release(BiNode *bt);//析构函数调用
	void preOrder(BiNode *bt);//前序遍历函数调用
	void inOrder(BiNode *bt); //中序遍历函数调用
	void postOrder(BiNode *bt);//后序遍历函数调用
};

二叉树的遍历：从根结点出发，按照某种次序访问二叉树中的所有结点，使得每个结点被访问一次且仅被访问一次

访问：抽象操作，可以是对结点进行的各种处理，这里简化为输出结点的数据

二叉树遍历操作的结果：非线性结构线性化

二叉树的组成

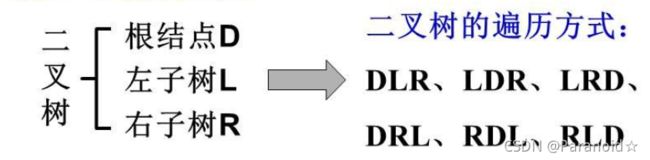
如果限定先走后右，则二叉树的遍历有三种:
(1)前序：DLR
(2)中序：LDR
(3)后序：LRD
(4)层序遍历：按照二叉树的层序编号的次序访问各结点

前序遍历

若二叉树为空，则空操作返回；否则：
(1)访问根节点
(2)前序遍历根节点的左子树
(3)后序遍历根节点的右子树

前序遍历序列：A–>B–>D–>G–>C–>E–>F

前序遍历递归算法

void BiTree::PreOrder(BiNode *bt)
{
    if(bt==NULL)   // 递归调用的结束的条件
    {
        return;
    }
    else
    {
        visit(bt->data);      // 访问根结点的bt的数据域
        PreOrder(bt->lchild); // 前序递归遍历bt的左子树
        PreOrder(bt->rchild); // 前序递归遍历bt的右子树
    }
}

注：这里visit(bt->data)，直接对该结点进行输出(printf())即可

中序遍历

若二叉树为空，则空操作返回；否则：
(1)中序遍历根节点的左子树
(2)访问根节点
(3)中序遍历根节点的右子树

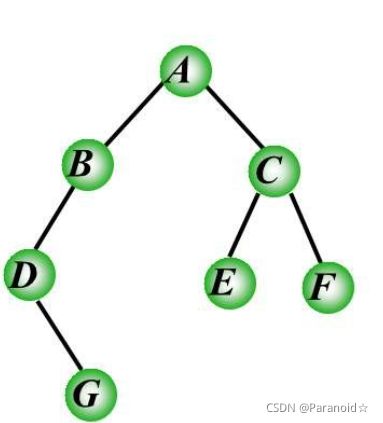
中序遍历序列：D–>G–>B–>A–>E–>C–>F

中序遍历递归算法

void BiTree::InOrder(BiNode *bt)
{
    if(bt==NULL)  // 递归调用的结束的条件
    {
        return;
    }
    else
    {
        InOrder(bt->lchild); // 中序递归遍历bt的左子树
        visit(bt->data);     // 访问根结点的bt的数据域
        InOrde(bt->rchild);  // 中序递归遍历bt的右子树
    }
}

后序遍历

若二叉树为空，则空操作返回；否则：
(1)后序遍历根节点的左子树
(2)后序遍历根节点的右子树
(3)访问根节点

后序遍历序列：G–>D–>B–>E–>F–>C–>A

后序遍历递归算法

void BiTree::PostOrder(BiNode *bt)
{
    if(bt==NULL)       // 递归调用的结束的条件
    {
        return;
    }
    else
    {
        PostOrder(bt->lchild);   // 后序递归遍历bt的左子树
        PostOrder(bt->rchild);   // 后序递归遍历bt的右子树
        visit(bt->data);         // 访问根结点的bt的数据域
    }
}

层序遍历

二叉树的层序遍历是指从二叉树的第一层（即根结点开始），从上至下逐层遍历，在同一层中，则按照从左到右的顺序对结点逐个进行访问

层序遍历序列：A–>B–>C–>D–>E–>F–>G

遍历实现描述过程：
1.队列Q初始化
2.如果二叉树非空，将根指针入队
3. 循环直到队列为空
（1）q= 队列Q的队头元素出队
（2) 访问结点的q的数据域
（3）若q不存在左孩子，则将左孩子指针入队
（4）若q不存在右孩子，则将右孩子指针入队

层序遍历算法

void BiTree::LeverOrder()
{
    if(root==NULL) return;     // 二叉树为空，程序结束
    queue.enQueue(root);       // 根指针入队
    while(!queue.isEmpty())    // 当队列不为空
    {
        q=queue.deQueue();     // 出队
        visit(q->data);
        if(q->lchild!=NULL)
        {
            queue.deQueue(q->lchild); //左孩子入队
        }
        if(q->rchild!=NULL)
        {
            queue.deQueue(q->rchild); // 右孩子入队
        }
    }
}

二叉树的非递归遍历

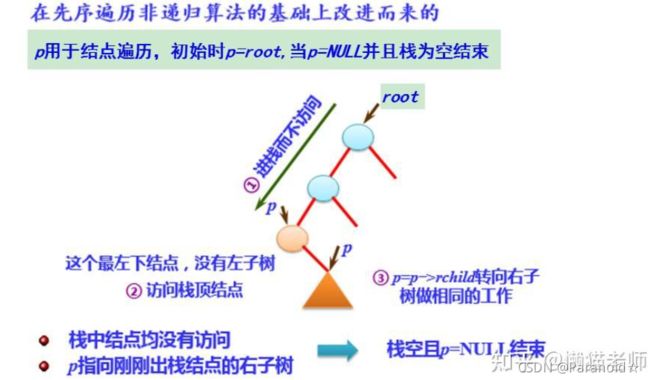
前序遍历

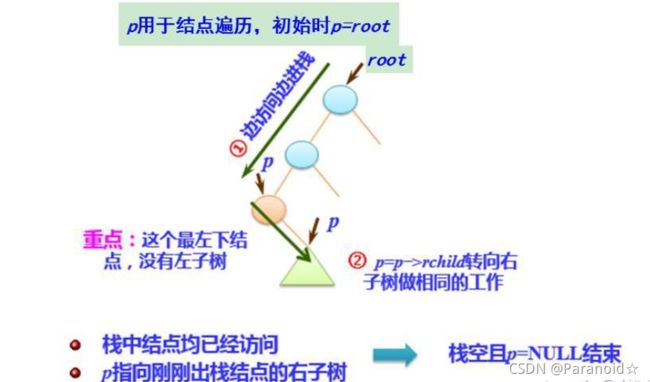
二叉树前序遍历的非递归算法的关键：在前序遍历完某结点的整个左子树后，如何找到该结点的右子树。

解决办法：在访问完该结点后，将该结点的指针保存在栈中，以便后面能通过它找到该结点的右子树

算法描述：

1. 栈s初始化

2. 循环直到p为空且栈s为空:
   (1).当p不为空时循环
   a.访问p->data
   b.将指针p的值保存道栈中
   c.继续遍历p的左子树

   (2)如果栈s不为空
   a.将栈顶元素弹出至p
   b.准备遍历p的右子树

算法实现

void BiTree::PreOrder()
{
    Stack s;
    p=root;
    while(p!=NULL||!is.Empty())  // 当p为空且栈也为空时退出循环
    {
        while(p!=NULL)          // 一直访问并移动指针p,直到遇到最左叶子的左指针，结束循环
        {
            visit(p->data);     // 访问根结点
            s.push(p);          // 将指针p的结点压入栈
            p=p->lchild;        // 遍历左子树
        }
        if(!is.Empty())         // 栈不为空
        {
            p=s.pop();          // 根结点出栈
            p=p->rchild;        // 遍历右结点
        }
    }
}

中序遍历

在二叉树的中序遍历中，访问结点的操作发生在该结点的左子树遍历完毕并准备遍历右子树时，所以, 在遍历过程中遇到某结点时并不能立即访问它，而是将它压栈，等到它的左子树遍历完毕后,再从栈中弹出并访问之。中序遍历的非递归算法只需将前序遍历的非递归算法中的输出语句visit(bt->data)移到p = s.pop();之后即可

中序遍历非递归算法

void BiTree::InOrder()
{
    Stack s;
    p=root;
    while(p!=NULL||!is.Empty()) // 当p为空并且栈为空时退出循环
    {
        while(p!=NULL)          // 一直移动指针p，直到遇到最左叶子的左指针，结束循环
        {
            s.push(p);          // 将指针p的值压入栈中
            p=p->lchild;        // 遍历左子树，但是不访问
        }
        if(!s.Empty())
        {
            p=s.pop();          // 根节点出栈
            visit(p->data);     // 访问根结点
            p=p->rchild;        // 遍历右子树
        }
    }
}

后序遍历

在后序遍历过程中，结点要入两次栈，出两次栈：

(1）第一次出栈:
只遍历完左子树，该结点不出栈，利用栈顶结点找到它的右子树，准备遍历它的右子树

(2)第二次出栈:
遍历完右子树，将该结点出栈，并访问它，所以，为了区别同一个结点的两次出栈，设置标志flag

栈元素结构

struct element
{
	BiNode *ptr;
	int flag;  // flag=1:第一次出栈 flag=2:第二次出栈
}

后序遍历非递归算法

void BiTree::postOrder()
{
    Stack s;
    p=root;
    while(p!=NULL||!s.Empty())     // 当p为空并且栈为空时退出循环
    {
        if(p!=NULL)                // 第一次入栈访问左子树
        {
            elem.ptr=p;
            elem.flag=1;           // 第一次入栈
            s.push(elem);
            p=p->lchild;           // 访问左孩子
        }
        else
        {
            elem=s.pop();          // 出栈
            p=elem.ptr;            // p指向当前要处理的结点
            if(elem.flag==1)
            {
                //flag==1:只访问过左子树，还要继续访问右子树
                elem.flag=2;      // flag =2 ：将第二次入栈
                s.push(elem);
                p=p->rchild;      // 访问右孩子
            }
            else  // flaf = 2 :左右子树均被访问，最后访问父结点
            {
                visit(p->data);    // 访问该结点的数据域
                p=NULL;            // 访问后将p=NULL为了确保下次循环时继续出栈，返回到上一级
            }
        }
    }
}

---

总结

提示：这里对文章进行总结：