【数据结构与算法-递归、回溯、分治策略面试经典例题汇总】
【数据结构与算法-递归、回溯、分治策略经典例题汇总】
-
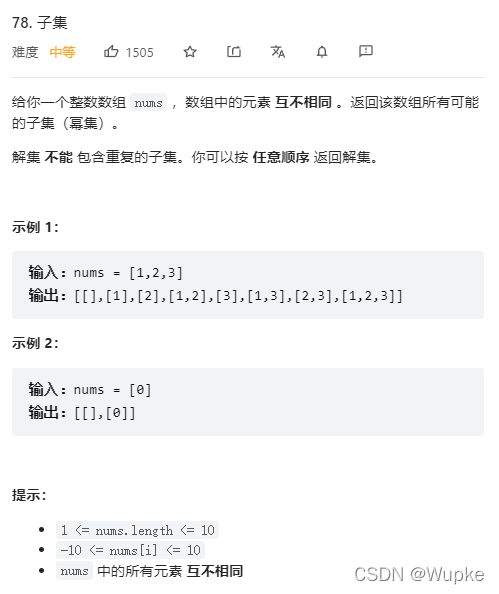
- 典例1、求子集（medium）
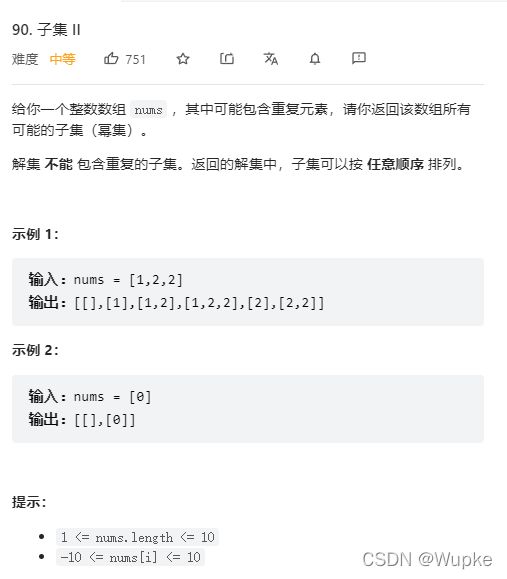
- 典例2、求子集-2（medium）
- 典例3、组合数之和2（medium）
- 典例4、生成括号（medium）
- 典例5、N皇后（hard）*
- 典例6、逆序数（hard）
-
基础点击：
-
递归三要素
① 递归算法包含一个基本结束条件（最小规模问题直接可以解决）
② 递归算法必须能改变状态，向基本结束条件演进（在不断的减小问题的规模）
③ 递归算法必须调用自身（即是解决减小规模的相同问题） -
示例： 递归计算 1 + 2 + 3 的和
# include- 回溯法
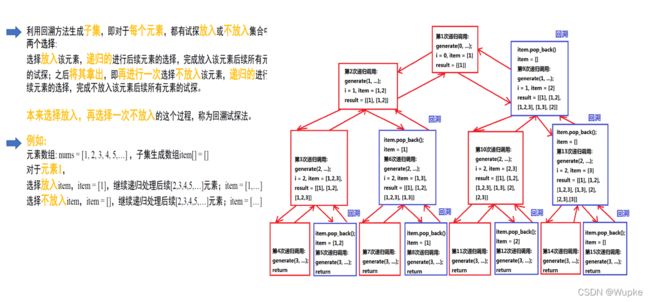
- 又称为试探法，当探索到某一步时候，发现原先的选择不能实现预期目标，就退回一步重新选择，这种走不通就退回再走的方法就是回溯法。
典例1、求子集（medium）
-
题目描述：
-
思路：
-
LeetCode提交OJ测试链接:
-
OJ测试代码实现：
class Solution {
private:
// 声明递归回溯的过程
void generate(int i,std::vector<int>& nums, // i 为选择给定数组nums中元素的个数
std::vector<int>& item, // 回溯过程中产生的子集
std::vector<std::vector<int>>& result){//最终产生的结果
if (i>=nums.size()){ // 递归结束条件
return ;
}
item.push_back(nums[i]); // 将当前元素压入vector形成子集
result.push_back(item); // 将形成子集压入结果vector 存储
generate(i+1,nums,item,result);// 第一次递归调用
item.pop_back(); // 回撤一步
generate(i+1,nums,item,result); // 第二次递归调用
}
public:
vector<vector<int>> subsets(vector<int>& nums) {
std::vector<std::vector<int>> result;//存储最终的结果
std::vector<int> item;//递归回溯过程中产生的子集
result.push_back(item);//先压入空集到结果result中
generate(0,nums,item,result); // 依次递归计算得到各个子集
return result;
}
};
- 完整的本地代码：
典例2、求子集-2（medium）
-
题目描述：
-
思路：
-
LeetCode提交OJ测试链接:
-
OJ测试代码实现：
class Solution {
private:
void generate(int i,std::vector<int> &nums,std::vector<int>& item,
std::vector<std::vector<int>> &result,
std::set<std::vector<int>> &res_set){ // 如果res_set集合中无item，（无重复的item）
if(i>=nums.size()){return ;}
item.push_back(nums[i]);
if(res_set.find(item)==res_set.end()){ //判断当前的子集是否在之前出现过？
result.push_back(item); //将item放入result
res_set.insert(item); // 将item放入去重集合res_set中
}
generate(i+1,nums,item,result,res_set);
item.pop_back();
generate(i+1,nums,item,result,res_set);
}
public:
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
std::vector<std::vector<int>> result;
std::vector<int> item;
std::set<std::vector<int>> res_set; // 去重使用的结合set
sort(nums.begin(),nums.end()); // 堆nums进行排序
result.push_back(item);// 加入空集
generate(0,nums,item,result,res_set);
return result;
}
};
- 完整的本地代码：
典例3、组合数之和2（medium）
-
题目描述：
-
思路：
-
基本思路：按照典例2中的思路，先构造出所有的无重复子集，再依据子集的和为target的进行筛选。
-
在此基础上可以进行代码优化剪枝，注意剪枝应该在生成子集和的时候就进行剪枝，即搜索的过程中就去掉重复组合。
-
LeetCode提交OJ测试链接:
-
OJ测试代码实现：
-
构造出所有的无重复子集，再依据子集的和进行筛选
-
即是先对数组排序，组合的所有子集中用set进行去重
class Solution {
private:
void generate(int i,std::vector<int>&candidates,
std::vector<int>&item,
std::vector<std::vector<int>> &result,
std::set<std::vector<int>>& res_set){
if (i>candidates.size()){return;} //递归结束条件
item.push_back(candidates[i]);
// if (compute_sum(item)==target && res_set.find(item)==res_set.end()){
if (res_set.find(item)==res_set.end()){ // 核查无重复子集
result.push_back(item);
res_set.insert(item);
}
generate(i+1,candidates,item,result,res_set); // 第一次调用递归
item.pop_back(); //回溯
generate(i+1,candidates,item,result,res_set);// 第二次调用递归
}
// void compute_sum(int i,std::vector &sum){
// if(i>item.size()){return;}
// sum +=i;
// compute_sum(i+1,sum);
// }
public:
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
std::vector<int>item; // lishi ziji
std::vector<std::vector<int>> result; // 存储所有不重子集
std::set<std::vector<int>> res_set;// 使用set去重
std::sort(candidates.begin(),candidates.end()); // 先排序
generate(0,candidates,item,result,res_set);
std::vector<std::vector<int>> target_result; //储存最终结果
for(int i=0;i<result.size();i++){ //计算各个子集的和
int sum = 0;
for(int j=0;j<result[i].size(); j++){
sum += result[i][j];
}
if (sum==target){ // 将符合和为target的子集添加到target_result
target_result.push_back(result[i]);
}
}
return target_result;
}
};
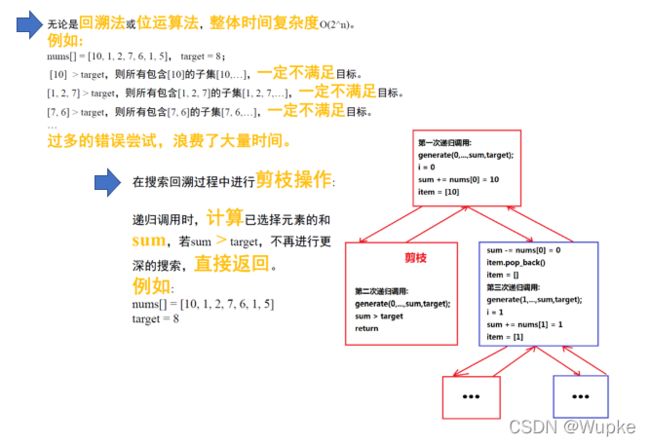
- 剪枝优化代码（遇到不符合的子集，提前结束）
class Solution {
private:
void generate(int i,std::vector<int>&candidates,
std::vector<int>&item,
std::vector<std::vector<int>> &result,
std::set<std::vector<int>>& res_set,int sum, int target){
if (i>candidates.size() || sum > target){return;} //递归结束条件：当所给的集合中元素已经选完，或者sum和超过target(sum为当前子集的和)
sum += candidates[i];
// if (i ==candidates.size() && candidates[i] > target){return ;}
item.push_back(candidates[i]);
if (target==sum && res_set.find(item)==res_set.end()){ // 核查无重复子集，当item的元素和为target且结果未添加进时
result.push_back(item); // 添加入最终的结果集合
res_set.insert(item); // 添加进set中，去除重复
}
generate(i+1,candidates,item,result,res_set,sum,target); // 第一次调用递归
sum -= candidates[i]; // 回溯时，要从sum中减去当前回撤的元素candidates[i]
item.pop_back(); // 并从子集item 中删去该元素
generate(i+1,candidates,item,result,res_set,sum,target);// 第二次调用递归
}
public:
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
std::vector<int>item; // 元素形成的临时子集
std::vector<std::vector<int>> result; // 存储最终结果的不重复子集
std::set<std::vector<int>> res_set;// 使用set去重
std::sort(candidates.begin(),candidates.end()); // 先排序
generate(0,candidates,item,result,res_set,0,target); // 递归调用，sum从零开始
return result;
}
};
- 完整的本地代码：
典例4、生成括号（medium）
- 题目描述：
- 思路：
打印生成所有结果
#include 
-
一定是先放左括号的递归；
-
还要注意什么时候才能放右括号的递归；
-
LeetCode提交OJ测试链接:
-
OJ测试代码实现：
class Solution {
private:
// 定义函数，生成合法的字符串
void generate(std::string item,int left,int right,
std::vector<std::string> &result){ // left:当前还可以放左括号的数量；right 当前还可以放右括号的数量
if (left==0 && right == 0){ // 当 合法的括号字符串都放完毕时候，结束递归
result.push_back(item); // 存入合法结果
return;
}
if(left>0){ // 合法的括号顺序一定是先放左括号
generate(item+'(',left-1,right,result);
}
if(left<right){ // （什么时候会放右括号）当 左括号可放数<右括号，才会放右括号
generate(item +')',left,right-1,result);
}
}
public:
std::vector<std::string> generateParenthesis(int n) {
std::vector<std::string> result; // 存储合法字符串
generate("",n,n,result); //递归调用
return result;
}
};
- 完整的本地代码：
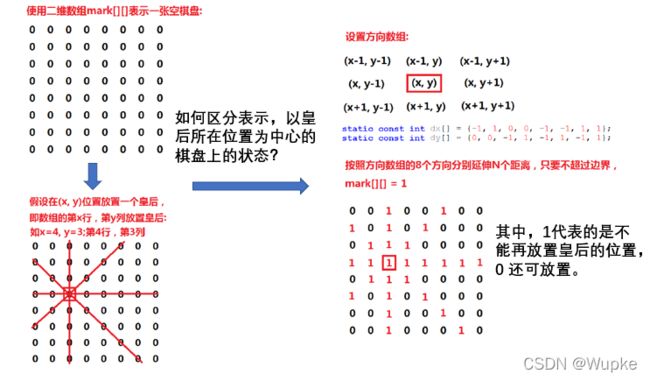
#include 典例5、N皇后（hard）*
-
题目描述：
-
思路：递归+回溯
-
理解棋盘上放置一个皇后以后棋盘的状态：
- 方向数字：
行更新：【上，下，左，右，左上，右上，左下，右下】
相应的行数坐标：【-1，+1,0，0，-1，-1，+1，+1 】
列更新相同。
-
LeetCode提交OJ测试链接:
-
OJ测试代码实现：
class Solution{
private:
// 放置皇后以后，改变连锁的坐标状态
void put_down_the_queen(int x,int y,std::vector<std::vector<int> > &mark){
// 设置方向数组
static const int dx[] = {-1,1,0,0,-1,-1,1,1};// 行坐标差（上下左右，左上右上左下右下）
static const int dy[] = {0,0,-1,1,-1,1,-1,1};// 列坐标差（上下左右，左上右上左下右下）
mark[x][y] = 1;// 放置Queen的坐标
for(int i = 1; i < mark.size(); i++){// 8个方向，每个方向向外延伸1至N-1
for(int j=0;j < 8; j++){
int new_x = x + i*dx[j];
int new_y = y + i*dy[j];
if(new_x>=0 && new_x <mark.size() && new_y >=0 && new_y < mark.size()){ // 确保坐标还在棋盘内
mark[new_x][new_y] = 1; // 将右Queen放置引起的连锁坐标状态更改
}
}
}
}
// 递归回溯 各行皇后的位置
void generate(int k,int n,// k 代表完成了几个皇后位置放置（正在放置第k行皇后）
std::vector<std::string> &location,//某次结果存储在location中
std::vector<std::vector<std::string> > &result,//最终结果存储在result中
std::vector<std::vector<int> > &mark){//表示棋盘的标记数组
if(k==n){ // 当 K == n时，代表完成了0至n-1行的放置，所有皇后放置完成后，将记录皇后位置的location数组push进result
result.push_back(location); //
return;
}
for(int i=0;i<n;i++){ // 按照顺序尝试0到n-1列
if(mark[k][i] == 0){ // 若 mark[k][i] == 0， 就是可以放置皇后
std::vector<std::vector<int> > temp_mark = mark;//记录回溯前的mark镜像
location[k][i] = 'Q';//记录当前皇后的位置
put_down_the_queen(k,i,mark);//放置皇后
generate(k+1,n,location,result,mark);//递归下一行皇后位置
// 回溯
mark = temp_mark; // 将Mark重新赋值为回溯前的状态
location[k][i] ='.';// 将尝试前的皇后位置重新置为'·'
}
}
}
public:
std::vector<std::vector<std::string> > solveNQueens(int n){
std::vector<std::vector<std::string> > result;//存储最终结果的数组
std::vector<std::vector<int> > mark;//标记棋盘是否可以放置皇后的二维数组
std::vector<std::string> location;//存储某个摆放结果，当完成一次递归找到结果后，将location push进入result
for(int i=0;i<n;i++){
mark.push_back((std::vector<int>()));
for(int j=0;j<n;j++){
mark[i].push_back(0); //初始化棋盘0
}
location.push_back("");
location[i].append(n,'.'); //初始化存放皇后位置的字符
}
generate(0,n,location,result,mark);
return result;
}
};
- 完整的本地测试代码：
#include典例6、逆序数（hard）
- 题目描述：
预备知识：
-
基础：分治策略
-
将一个规模为 N 的问题分解为 K 个规模较小的子问题，这些子问题相互独立，且与原问题性质相同。求出子问题的解后进行合并，就可以得到原问题的解。
分治的步骤：
1、分解，将要解决的问题划分成若干个规模较小的同类问题；
2、求解，当子问题划分的足够小时，用较简单的方法解决；
3、合并，按原问题的要求，将子问题的解逐渐合并构成原问题的解。
-
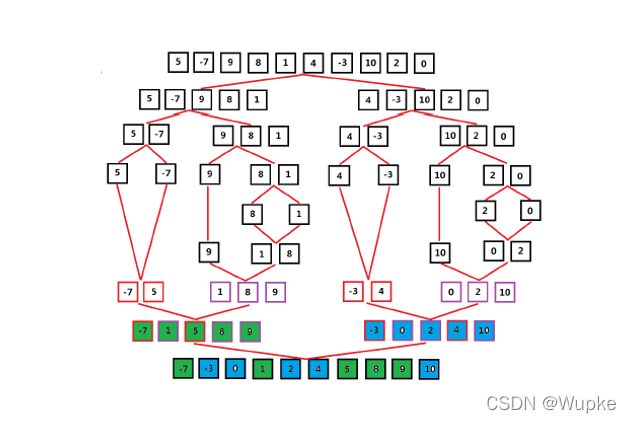
归并排序的复杂度：
设n 个元素，n 个元素归并排序的时间为T(n) ； -
总时间 = 分解时间+解决子问题时间+合并时间
T(n) = O(n) + 2T(n/2) + O(n)
= 2T(n/2) + 2O(n)
= O(nlogn)
# 归并排序=示例
#include本题思路：
- 解决顺序混乱了的问题：
-
LeetCode提交OJ测试链接:
-
OJ测试代码实现：
-
注意 std::pair 的用法.
class Solution{
public:
std::vector<int> countSmaller(std::vector<int> &nums){
std::vector<std::pair<int,int> > vec;
std::vector<int> count;
for(int i=0; i< nums.size(); i++){
vec.push_back(std::make_pair(nums[i],i));
count.push_back(0);
}
merge_sort(vec,count);
return count;
}
private:
void merge_sort_two_vec(
std::vector<std::pair<int,int> > &sub_vec1,
std::vector<std::pair<int,int> > &sub_vec2,
std::vector<std::pair<int,int> > &vec,
std::vector<int> &count){//数组1，数组2，合并后的数组, 计数
int i=0;
int j = 0;
while( i<sub_vec1.size() && j<sub_vec2.size() ){
if(sub_vec1[i].first <=sub_vec2[j].first ){
count[sub_vec1[i].second] += j;
vec.push_back(sub_vec1[i]); //sub_vec1[i] 小，则压入合并后的数组
i++;
}
else{
vec.push_back(sub_vec2[j]);
j++;
}
}
for( ; i < sub_vec1.size(); i++ ){ //sub_vec1 有剩余，将余下的元素则压入vec
count[sub_vec1[i].second] += j;
vec.push_back(sub_vec1[i]);
}
for( ; j < sub_vec2.size(); j++ ){//sub_vec2 有剩余，将余下的元素则压入vec
vec.push_back(sub_vec2[j]);
}
}
void merge_sort(std::vector<std::pair<int,int> > &vec,
std::vector<int> &count){
if (vec.size()<2){
return ; // 1、求解的问题足够小时，直接解决
}
int mid = vec.size() / 2 ; //2、拆解问题大小
std::vector<std::pair<int,int> > sub_vec1;
std::vector<std::pair<int,int> > sub_vec2;
for(int i=0;i<mid;i++){ // 前半部分放进 sub_vec1;
sub_vec1.push_back(vec[i]);
}
for(int i=mid;i<vec.size();i++){ // 后半部分放进 sub_vec2;
sub_vec1.push_back(vec[i]);
}
merge_sort(sub_vec1,count); //对拆解后的两个子问题进行求解
merge_sort(sub_vec2,count);
vec.clear();
merge_sort_two_vec(sub_vec1,sub_vec2,vec,count); // 3、合并，将子问题的解进行合并
}
};