【算法与数据结构】538、LeetCode把二叉搜索树转换为累加树

所有的LeetCode题解索引，可以看这篇文章——【算法和数据结构】LeetCode题解。

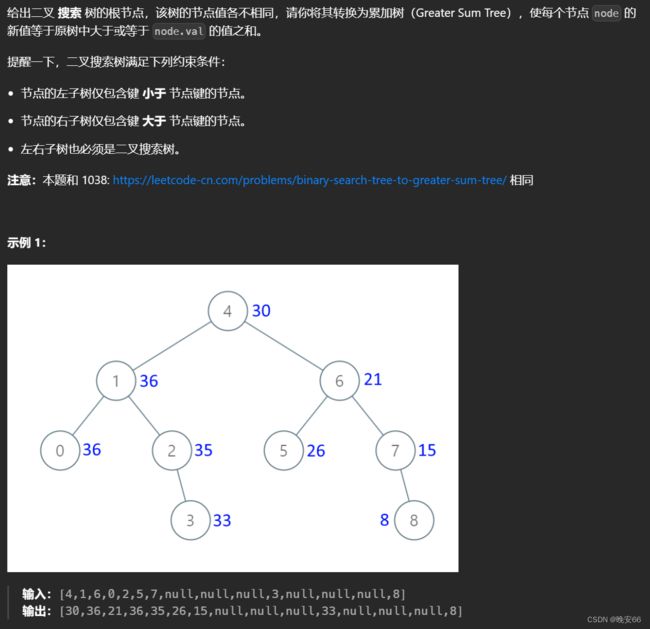
一、题目

二、两个解法

  思路分析：本题笔者想了一个很笨的方法，遍历的两次二叉树，依次用来记录二叉树的值，另一次用来修改二叉树的值。首先我们先遍历一次，将二叉搜索树的值存放在数组当中，然后再次遍历，用累加求和，修改二叉树的值。
  程序如下：

class Solution {
public:
    void traversal_midOrder(TreeNode* cur, vector<int>& vec) {
        if (cur == NULL) return;
        traversal_midOrder(cur->left, vec);     // 左
        vec.push_back(cur->val);                // 中
        traversal_midOrder(cur->right, vec);    // 右
    }
    void traversal_midOrder_sum(TreeNode* cur, vector<int>& vec) {
        if (cur == NULL) return;
        traversal_midOrder_sum(cur->left, vec);     // 左
        int sum = 0;
        for (int i = 0; i < vec.size(); i++) {  // 中           
            if (vec[i] >= cur->val) {
                sum += vec[i];
            }
        }
        cur->val = sum;
        traversal_midOrder_sum(cur->right, vec);    // 右
    }
    // 中序遍历得到有序数组，然后再次中序遍历，加上对应值
    TreeNode* convertBST(TreeNode* root) {
        vector<int> v;
        traversal_midOrder(root, v);
        traversal_midOrder_sum(root, v);
        return root;
    }
};

复杂度分析：

• 时间复杂度： $O(n)$，遍历两次，$O(2n)=O(n)$。
• 空间复杂度：$O(n)$。

  思路分析：经过一番思索，二叉搜索树的中序遍历时一个有序数组，累加实际上是把后序遍历数组中大于等于节点键值的值累加，然后重新赋值给节点。实际上这种累加就是后序累加，[1, 2, 3]变成[6, 5, 3]。那么我们用右中左这种反中序遍历的方式遍历二叉搜索树。程序还是用递归实现，反后序遍历会先找到最大的那个节点(最大节点的累计值等于本身，因此pre初始化为0)，然后令当前节点加上上一个节点的值，更新pre，反复递归。
  程序如下：

class Solution2 {
private:
    int pre = 0; // 记录前一个节点的数值
    void traversal(TreeNode* cur) { // 右中左遍历
        if (cur == NULL) return;
        traversal(cur->right);
        cur->val += pre;
        pre = cur->val;
        traversal(cur->left);
    }
public:
    TreeNode* convertBST(TreeNode* root) {
        pre = 0;
        traversal(root);
        return root;
    }
};

复杂度分析：

• 时间复杂度： $O(n)$，遍历一次。
• 空间复杂度：$O(n)$。

三、完整代码

# include 
# include 
# include 
# include 
using namespace std;

// 树节点定义
struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode* left, TreeNode* right) : val(x), left(left), right(right) {}
};

class Solution {
public:
    void traversal_midOrder(TreeNode* cur, vector<int>& vec) {
        if (cur == NULL) return;
        traversal_midOrder(cur->left, vec);     // 左
        vec.push_back(cur->val);                // 中
        traversal_midOrder(cur->right, vec);    // 右
    }
    void traversal_midOrder_sum(TreeNode* cur, vector<int>& vec) {
        if (cur == NULL) return;
        traversal_midOrder_sum(cur->left, vec);     // 左
        int sum = 0;
        for (int i = 0; i < vec.size(); i++) {  // 中           
            if (vec[i] >= cur->val) {
                sum += vec[i];
            }
        }
        cur->val = sum;
        traversal_midOrder_sum(cur->right, vec);    // 右
    }
    // 中序遍历得到有序数组，然后再次中序遍历，加上对应值
    TreeNode* convertBST(TreeNode* root) {
        vector<int> v;
        traversal_midOrder(root, v);
        traversal_midOrder_sum(root, v);
        return root;
    }
};

class Solution2 {
private:
    int pre = 0; // 记录前一个节点的数值
    void traversal(TreeNode* cur) { // 右中左遍历
        if (cur == NULL) return;
        traversal(cur->right);
        cur->val += pre;
        pre = cur->val;
        traversal(cur->left);
    }
public:
    TreeNode* convertBST(TreeNode* root) {
        pre = 0;
        traversal(root);
        return root;
    }
};

// 前序遍历迭代法创建二叉树，每次迭代将容器首元素弹出（弹出代码还可以再优化）
void Tree_Generator(vector<string>& t, TreeNode*& node) {
    if (!t.size() || t[0] == "NULL") return;    // 退出条件
    else {
        node = new TreeNode(stoi(t[0].c_str()));    // 中
        if (t.size()) {
            t.assign(t.begin() + 1, t.end());
            Tree_Generator(t, node->left);              // 左
        }
        if (t.size()) {
            t.assign(t.begin() + 1, t.end());
            Tree_Generator(t, node->right);             // 右
        }
    }
}

template<typename T>
void my_print(T& v, const string msg)
{
    cout << msg << endl;
    for (class T::iterator it = v.begin(); it != v.end(); it++) {
        cout << *it << ' ';
    }
    cout << endl;
}

template<class T1, class T2>
void my_print2(T1& v, const string str) {
    cout << str << endl;
    for (class T1::iterator vit = v.begin(); vit < v.end(); ++vit) {
        for (class T2::iterator it = (*vit).begin(); it < (*vit).end(); ++it) {
            cout << *it << ' ';
        }
        cout << endl;
    }
}

// 层序遍历
vector<vector<int>> levelOrder(TreeNode* root) {
    queue<TreeNode*> que;
    if (root != NULL) que.push(root);
    vector<vector<int>> result;
    while (!que.empty()) {
        int size = que.size();  // size必须固定, que.size()是不断变化的
        vector<int> vec;
        for (int i = 0; i < size; ++i) {
            TreeNode* node = que.front();
            que.pop();
            vec.push_back(node->val);
            if (node->left) que.push(node->left);
            if (node->right) que.push(node->right);
        }
        result.push_back(vec);
    }
    return result;
}

int main()
{
    // 构建二叉树
    vector<string> t = { "4", "1", "0", "NULL", "NULL", "2", "NULL", "3", "NULL", "NULL", "6", "5", "NULL", "NULL", "7", "NULL", "8", "NULL", "NULL" };   // 前序遍历
    my_print(t, "目标树");
    TreeNode* root = new TreeNode();
    Tree_Generator(t, root);
    vector<vector<int>> tree = levelOrder(root);
    my_print2<vector<vector<int>>, vector<int>>(tree, "目标树:");

    // 转化为累加树目标值
    Solution s;
    TreeNode* result = s.convertBST(root);
    vector<vector<int>> tree1 = levelOrder(result);
    my_print2<vector<vector<int>>, vector<int>>(tree1, "结果树:");

    system("pause");
    return 0;
}

end