Java 栈和队列

栈和队列

栈

• 定义：一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。栈中的数据元素遵守 后进先出 LIFO（Last In First Out）的原则

• 压栈：栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶

• 出栈：栈的删除操作叫做出栈。出数据在栈顶

• 栈的常用操作：
  

public class StackDemo {
    public static void main(String[] args) {
        Stack<Integer> stack = new Stack<>();
        //push(),压栈
        stack.push(1);
        stack.push(2);
        stack.push(3);
        stack.push(4);
        stack.push(5);
        System.out.println(stack);

        //pop()，弹出栈顶元素并返回
        System.out.println(stack.pop());
        System.out.println(stack);

        //peek(),得到栈顶元素不弹出
        System.out.println(stack.peek());
        System.out.println(stack);

        //判断是否为空
        System.out.println(stack.empty());

        //查找返回一个对象在此堆栈上的基于1的位置
        System.out.println(stack.search(3));
    }
}

• 实现一个简单的顺序栈（数组实现）

class MyStack{
    public int[] elem;
    public int top;

    public MyStack() {
        this.elem = new int[5];
        this.top = 0;
    }

    public void push(int item){
        if (this.isFull()){
            return;
        }
        this.elem[top++] = item;
    }

    public int pop(){
        if (this.empty()){
            throw new RuntimeException("栈为空...");
        }
        int index = this.top - 1;
        this.top--;
        return this.elem[index];
    }

    public boolean empty(){
        return this.top == 0;
    }

    public int peek(){
        if (this.empty()){
            throw new RuntimeException("栈为空...");
        }
        return this.elem[this.top-1];
    }

    public boolean isFull() {
        return this.top == this.elem.length;
    }

}

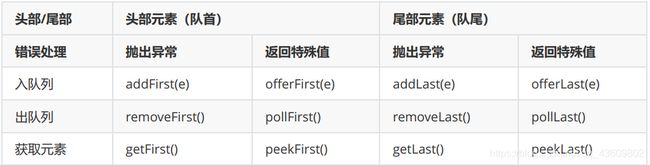
队列

• 定义：只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列具有先进先出FIFO(FirstIn First Out) 入队列：进行插入操作的一端称为队尾（Tail/Rear） 出队列：进行删除操作的一端称为队头
  

• 实现一个简单的队列（链表实现）
  

class Node{
    public int val;
    public Node next;

    public Node(int val) {
        this.val = val;
    }
}

class MyQueue{
    public Node head;
    public Node tail;

    public void offer(int val){
        Node node = new Node(val);
        if (this.head == null){
            this.head = node;
            this.tail = node;
            return;
        }
        this.tail.next = node;
        this.tail = node;
    }

    public int poll() {
        if (this.isEmpty()){
            throw new RuntimeException("队列为空...");
        }
        int tmp = this.head.val;
        this.head = this.head.next;
        if (this.head == null){
            this.tail = null;
        }
        return tmp;
    }

    public int peek() {
        if (this.isEmpty()){
            throw new RuntimeException("队列为空...");
        }
        return this.head.val;
    }

    public boolean isEmpty() {
        return this.head == null;
    }
}

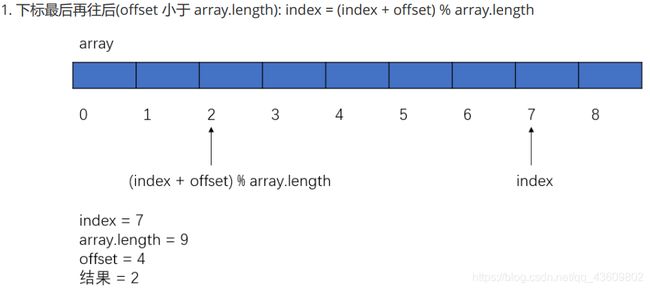
循环队列

使用数组要考虑好数组下标索引：

OJ链接：循环队列
代码简单实现：

class MyCircularQueue {

    public int[] elem;
    public int front;
    public int rear;

    /**
     * Initialize your data structure here. Set the size of the queue to be k.
     */
    public MyCircularQueue(int k) {
        this.elem = new int[k + 1];
    }

    /**
     * Insert an element into the circular queue. Return true if the operation is successful.
     */
    public boolean enQueue(int value) {
        //1、判断是否为满的
        if (isFull()) {
            return false;
        }
        //2、rear -->
        this.elem[this.rear] = value;
        this.rear = (this.rear + 1) % this.elem.length;
        return true;
    }

    /**
     * Delete an element from the circular queue. Return true if the operation is successful.
     */
    public boolean deQueue() {
        //1、是否为空   front和rear相遇的时候
        if (isEmpty()) {
            return false;
        }
        this.front = (this.front + 1) % this.elem.length;
        return true;
    }

    /**
     * Get the front item from the queue.
     */
    public int Front() {
        if (isEmpty()) {
            return -1;
        }
        return this.elem[this.front];
    }

    /**
     * Get the last item from the queue.
     */
    public int Rear() {
        if (isEmpty()) {
            return -1;
        }
        int index = this.rear == 0 ? this.elem.length - 1 : this.rear - 1;
        return this.elem[index];
    }

    /**
     * Checks whether the circular queue is empty or not.
     */
    public boolean isEmpty() {
        return front == rear;
    }

    /**
     * Checks whether the circular queue is full or not.
     */
    public boolean isFull() {
        return (this.rear + 1) % this.elem.length == this.front;
    }
}

• deque常用操作
  

常见题：

• 1.括号匹配
  • OJ链接：括号匹配
  • 解题思路：需要一个栈。用来存放左括号，然后进行匹配操作，但是需要考虑好各种情况

1、遇到左括号就入栈
2、遇到右括号，看一下栈顶元素的括号是否和当前右括号匹配---->匹配：出栈 不匹配：右括号匹配错误
3、直到整个字符串遍历完成
4、遍历完成后需要判断栈是否为空，栈不为空—>左括号多，为空—>返回true

public static boolean isValid(String s) {
    Stack<Character> stack = new Stack<>();
    for (int i = 0; i < s.length(); i++) {
        if (s.charAt(i)=='(' || s.charAt(i)=='[' || s.charAt(i)=='{'){
            stack.push(Character.valueOf(s.charAt(i)));
        } else {
            if (stack.empty()){    //右括号比左括号多的情况，栈为空
                return false;
            } else {
                char chLeft = stack.peek().charValue(); //左括号
                char chRight = s.charAt(i); //右括号
                if ((chLeft == '(' && chRight == ')') || (chLeft == '[' && chRight == ']') || (chLeft == '{' && chRight == '}')) {
                    stack.pop();    //匹配则出栈
                } else {
                    break;  //不匹配直接跳出
                }
            }
        }
    }
    return stack.empty();
}

当然还有更好的做法：

public boolean isValid(String s) {
    if(s.length()%2!=0){
        return false;
    }
    Stack<Character> stack = new Stack<>();
    for(char c : s.toCharArray()){
        //遇到左括号则将它对应的右括号入栈
        if(c=='{'){
            stack.push('}');
        } else if (c=='['){
            stack.push(']');
        } else if (c=='('){
            stack.push(')');
        } else if(stack.isEmpty() || c!=stack.pop()){
            return false;
        }
    }
    return stack.isEmpty();
}

• 2.实现一个最小栈
  • OJ链接：实现一个最小栈

• 设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。
  • push(x) —— 将元素 x 推入栈中。
  • pop() —— 删除栈顶的元素。
  • top() —— 获取栈顶元素。
  • getMin() —— 检索栈中的最小元素。

class MinStack {
    private Stack<Integer> stack;
    private Stack<Integer> minStack;
    /** initialize your data structure here. */
    public MinStack() {
        stack = new Stack<>();//入
        minStack = new Stack<>();//出
    }

    public void push(int x) {
        //1、stack是一定需要放元素的
        //2、最小栈当中 是否存放数据   x<= 最小栈的栈顶元素
        stack.push(x);
        if (minStack.empty()){
            minStack.push(x);
            return;
        }
        if (x <= minStack.peek()){
            minStack.push(x);
        }
    }

    public void pop() {
        //1、stack是一定需要弹出元素的
        //2、最小栈当中 是否弹出数据    x  ==  最小栈的栈顶元素
        int tmp = stack.pop();
        if (tmp == minStack.peek()){
            minStack.pop();
        }
    }

    public int top() {
        //跟最小栈没有关系
        return stack.peek();
    }

    public int getMin() {
        //每次返回最小栈的栈顶元素
        return minStack.peek();
    }
}