LeetCode231 2 的幂 / 第53场双周赛
231. 2 的幂
2021.5.30每日一题
题目描述
给你一个整数 n,请你判断该整数是否是 2 的幂次方。如果是,返回 true ;否则,返回 false 。
如果存在一个整数 x 使得 n == 2x ,则认为 n 是 2 的幂次方。
示例 1:
输入:n = 1
输出:true
解释:20 = 1
示例 2:
输入:n = 16
输出:true
解释:24 = 16
示例 3:
输入:n = 3
输出:false
示例 4:
输入:n = 4
输出:true
示例 5:
输入:n = 5
输出:false
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/power-of-two
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
昨天双周赛后看了一眼,今天每日一题就完事了
class Solution {
//这道题,来学两个技巧:
//第一个,x & (x-1) 这个操作使最右边的1变成0
//第二个,x & (-x) -x是x取反再加1, 这个操作取出来最右边的1,这两个都可以用在这道题
public boolean isPowerOfTwo(int n) {
if (n == 0) return false;
long x = (long) n;
return (x & (-x)) == x;
//return (x &(x - 1)) == 0;
}
}
第53场双周赛
咋说呢,昨天晚上在实验室做的,本来想着十二点关门,应该能撑过去,结果11点零几就来清人了,我…然后就着急着回去宿舍,打开电脑,结果不知道咋的黑屏了,又搞了十分钟, 一折腾二三十分钟没了。但是昨天做的还是不如意,前两道题还算顺利吧,第三道也就是个模拟,结果测试用例都一下过了,最后提交是错的,又把我弄懵了,到了十二点还没看出来。结果十二点一过,我再看,就知道问题在哪了,最后1200多名,如果第三道过了,估计应该能六七百吧,有点时间说不定还能做出来最后一道哈哈,还是有点遗憾,今天周赛再加油吧
5754. 长度为三且各字符不同的子字符串
题目描述
如果一个字符串不含有任何重复字符,我们称这个字符串为 好 字符串。
给你一个字符串 s ,请你返回 s 中长度为 3 的 好子字符串 的数量。
注意,如果相同的好子字符串出现多次,每一次都应该被记入答案之中。
子字符串 是一个字符串中连续的字符序列。
示例 1:
输入:s = "xyzzaz"
输出:1
解释:总共有 4 个长度为 3 的子字符串:"xyz","yzz","zza" 和 "zaz" 。
唯一的长度为 3 的好子字符串是 "xyz" 。
示例 2:
输入:s = "aababcabc"
输出:4
解释:总共有 7 个长度为 3 的子字符串:"aab","aba","bab","abc","bca","cab" 和 "abc" 。
好子字符串包括 "abc","bca","cab" 和 "abc" 。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/substrings-of-size-three-with-distinct-characters
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
一看字符串长度觉得暴力能过,直接写了暴力解
class Solution {
public int countGoodSubstrings(String s) {
int l = s.length();
int count = 0;
for(int i = 2; i < l; i++){
char a = s.charAt(i - 2);
char b = s.charAt(i - 1);
char c = s.charAt(i);
if(a != b && b != c && a != c){
count++;
}
}
return count;
}
}
5755. 数组中最大数对和的最小值
题目描述
一个数对 (a,b) 的 数对和 等于 a + b 。最大数对和 是一个数对数组中最大的 数对和 。
比方说,如果我们有数对 (1,5) ,(2,3) 和 (4,4),最大数对和 为 max(1+5, 2+3, 4+4) = max(6, 5, 8) = 8 。
给你一个长度为 偶数 n 的数组 nums ,请你将 nums 中的元素分成 n / 2 个数对,使得:
nums 中每个元素 恰好 在 一个 数对中,且
最大数对和 的值 最小 。
请你在最优数对划分的方案下,返回最小的 最大数对和 。
示例 1:
输入:nums = [3,5,2,3]
输出:7
解释:数组中的元素可以分为数对 (3,3) 和 (5,2) 。
最大数对和为 max(3+3, 5+2) = max(6, 7) = 7 。
示例 2:
输入:nums = [3,5,4,2,4,6]
输出:8
解释:数组中的元素可以分为数对 (3,5),(4,4) 和 (6,2) 。
最大数对和为 max(3+5, 4+4, 6+2) = max(8, 8, 8) = 8 。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/minimize-maximum-pair-sum-in-array
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
应该算是贪心吧,要想使得最大数对和最小,就是最大和最小配对。开始在考虑其他方法,过了一会还是反应过来了
class Solution {
public int minPairSum(int[] nums) {
//想多了,排序,然后从两边向中间求和
int l = nums.length;
Arrays.sort(nums);
int left = 0;
int right = l - 1;
int max = 0;
while(left < right){
max = Math.max(max, (nums[left] + nums[right]));
left++;
right--;
}
return max;
}
}
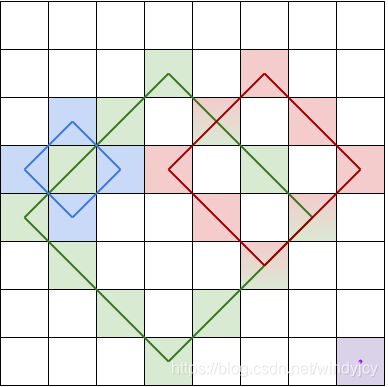
5757. 矩阵中最大的三个菱形和
题目描述
给你一个 m x n 的整数矩阵 grid 。
菱形和 指的是 grid 中一个正菱形 边界 上的元素之和。本题中的菱形必须为正方形旋转45度,且四个角都在一个格子当中。下图是四个可行的菱形,每个菱形和应该包含的格子都用了相应颜色标注在图中。
注意,菱形可以是一个面积为 0 的区域,如上图中右下角的紫色菱形所示。
请你按照 降序 返回 grid 中三个最大的 互不相同的菱形和 。如果不同的和少于三个,则将它们全部返回。
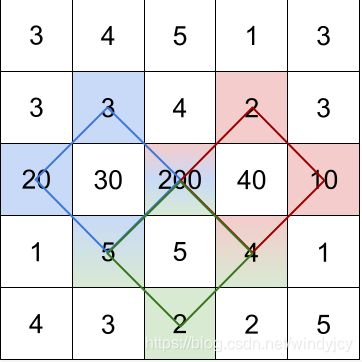
输入:grid = [[3,4,5,1,3],[3,3,4,2,3],[20,30,200,40,10],[1,5,5,4,1],[4,3,2,2,5]]
输出:[228,216,211]
解释:最大的三个菱形和如上图所示。
- 蓝色:20 + 3 + 200 + 5 = 228
- 红色:200 + 2 + 10 + 4 = 216
- 绿色:5 + 200 + 4 + 2 = 211
输入:grid = [[1,2,3],[4,5,6],[7,8,9]]
输出:[20,9,8]
解释:最大的三个菱形和如上图所示。
- 蓝色:4 + 2 + 6 + 8 = 20
- 红色:9 (右下角红色的面积为 0 的菱形)
- 绿色:8 (下方中央面积为 0 的菱形)
示例 3:
输入:grid = [[7,7,7]]
输出:[7]
解释:所有三个可能的菱形和都相同,所以返回 [7] 。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/get-biggest-three-rhombus-sums-in-a-grid
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
看到的第一眼想到的就是模拟,然后用一个数存储三个最大的值,因为是排序并且不重复的,也是这样实现的,可能代码有点复杂,但思路并不难,我当时写的代码是这样的
class Solution {
int m;
int n;
public int[] getBiggestThree(int[][] grid) {
TreeSet<Integer> set = new TreeSet<>();
m = grid.length;
n = grid[0].length;
int l = m < n ? (m + 1) / 2 : (n + 1) / 2;
//遍历所有的中心点
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
for(int k = 1; k <= l; k++){
int cur = 0;
if(k == 1)
cur = grid[i][j];
//左顶点
else{
int left = j - k + 1;
int right = j + k - 1;
int up = i - k + 1;
int down = i + k - 1;
if(!isinner(i, left) || !isinner(i, right) || !isinner(up, j) || !isinner(down, j))
continue;
cur = count(grid, i, j, left, right, up, down);
}
if(set.size() < 3)
set.add(cur);
else{
if(cur > set.first()){
set.pollFirst();
set.add(cur);
}
}
}
}
}
int[] res = new int[3];
int i = 0;
for(i = 0; i < 3; i++){
if(set.isEmpty())
break;
res[i] = set.pollLast();
}
return Arrays.copyOfRange(res, 0, i);
}
public boolean isinner(int i, int j){
return i >= 0 && i < m && j >= 0 && j < n;
}
public int count(int[][] a, int i, int j, int left, int right, int up, int down){
//从左边开始i,left > up,j
int res = 0;
for(int x = i; x > up; x--){
for(int y = left; y < j; y++)
res += a[x][y];
}
//up,j>i,right
for(int x = up; x < i; x++){
for(int y = j; y < right; y++)
res += a[x][y];
}
//i,right>down,j
for(int x = i; x < down; x++){
for(int y = right; y > j; y--)
res += a[x][y];
}
for(int x = down; x > i; x--){
for(int y = j; y > left; y--)
res += a[x][y];
}
return res;
}
}
测试用例都秒过,但是一提交就错,搞的我不知道改哪了,后面时间过了以后认真看了一下,发现计算边的时候,两层循环我是嵌套的…当时就给了自己十几拳
改了这个问题以后,再提交,最后一个测试用例没过,然后又看着给的答案想了半天,发现是添加到set集合中的时候,如果当前计算值,大于set中的最小值,但是却和set中其他值相同的话,也会添加到set集合中,导致这个值不会被记录下来,同时又把应该有的值给丢失了,所以需要在加入set集合那里加一句判断set中是否有当前元素这句话
唉,继续加油吧,做题的时候还是不能着急
class Solution {
int m;
int n;
public int[] getBiggestThree(int[][] grid) {
TreeSet<Integer> set = new TreeSet<>();
m = grid.length;
n = grid[0].length;
int l = m < n ? (m + 1) / 2 : (n + 1) / 2;
//遍历所有的中心点
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
for(int k = 1; k <= l; k++){
int cur = 0;
if(k == 1)
cur = grid[i][j];
//左顶点
else{
int left = j - k + 1;
int right = j + k - 1;
int up = i - k + 1;
int down = i + k - 1;
if(!isinner(i, left) || !isinner(i, right) || !isinner(up, j) || !isinner(down, j))
continue;
cur = count(grid, i, j, left, right, up, down);
}
if(set.size() < 3)
set.add(cur);
else{
if(!set.contains(cur) && cur > set.first()){
set.pollFirst();
set.add(cur);
}
}
}
}
}
int[] res = new int[set.size()];
for(int i = 0; i < res.length; i++){
res[i] = set.pollLast();
}
return res;
}
public boolean isinner(int i, int j){
return i >= 0 && i < m && j >= 0 && j < n;
}
public int count(int[][] a, int i, int j, int left, int right, int up, int down){
//从左边开始i,left > up,j
int res = 0;
for(int x = i, y = left; x > up; x--, y++){
//for(int y = left; y < j; y++)
res += a[x][y];
}
//up,j>i,right
for(int x = up, y = j; x < i; x++, y++){
//for(int y = j; y < right; y++)
res += a[x][y];
}
//i,right>down,j
for(int x = i, y = right; x < down; x++, y--){
//for(int y = right; y > j; y--)
res += a[x][y];
}
for(int x = down, y = j; x > i; x--, y--){
//for(int y = j; y > left; y--)
res += a[x][y];
}
return res;
}
}
5756. 两个数组最小的异或值之和
题目描述
给你两个整数数组 nums1 和 nums2 ,它们长度都为 n 。
两个数组的 异或值之和 为 (nums1[0] XOR nums2[0]) + (nums1[1] XOR nums2[1]) + ... + (nums1[n - 1] XOR nums2[n - 1]) (下标从 0 开始)。
比方说,[1,2,3] 和 [3,2,1] 的 异或值之和 等于 (1 XOR 3) + (2 XOR 2) + (3 XOR 1) = 2 + 0 + 2 = 4 。
请你将 nums2 中的元素重新排列,使得 异或值之和 最小 。
请你返回重新排列之后的 异或值之和 。
示例 1:
输入:nums1 = [1,2], nums2 = [2,3]
输出:2
解释:将 nums2 重新排列得到 [3,2] 。
异或值之和为 (1 XOR 3) + (2 XOR 2) = 2 + 0 = 2 。
示例 2:
输入:nums1 = [1,0,3], nums2 = [5,3,4]
输出:8
解释:将 nums2 重新排列得到 [5,4,3] 。
异或值之和为 (1 XOR 5) + (0 XOR 4) + (3 XOR 3) = 4 + 4 + 0 = 8 。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/minimum-xor-sum-of-two-arrays
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
这道题就在回去的路上简单想了想,觉得应该是位运算
但是今天看到数组长度最多14,突然事情没这么简单,感觉可以枚举
去看题解了,状态压缩dp,一时半会真看不懂,更别说自己想到了
31号又看了半天,终于有点眉目了。
首先看到数组长度最大为14,想到可以状压;然后把nums2中各位位置元素被选择的状态,定义成一个长度为n的二进制数mask。mask从低到高的第 i 位为1,说明nums2中国第 i 个位置的数被选择了
定义f[mask]为在nums2中选择元素状态为mask的情况下,并且选择了nums1中前count(mask)【表示mask中1的个数】个元素的情况下,组成的最小异或和
那么对于每一个状态,枚举此时选择的nums1中的元素也就是nums1[count(mask)],与nums2中哪一个元素进行了异或运算,并且在找到前面的状态,也就是让mask中(在nums2中选择元素的位置)为0,加起来就是当前的状态值,具体看代码
考虑完这个状态转移以后,再看状态定义,就会更加通透,状态定义是选择了nums1中前c个,nums2中是按mask选的,而状态转移呢,这2c个元素共有c的平方个组合,而状态转移让这种完全列举的情况,变成了c种,也就是从之前c-1的状态转移而来。即考虑两个数组中的第c个元素(从1开始),对于nums1中就是第c个,对于nums2中就是mask中1的位置;而前面c-1的状态,已经完成了,因为mask是从小到大增大的。
class Solution {
public int minimumXORSum(int[] nums1, int[] nums2) {
int n = nums1.length;
int[] dp = new int[(1 << n)];
Arrays.fill(dp, Integer.MAX_VALUE);
dp[0] = 0;
//遍历所有状态
for(int mask = 1; mask < (1 << n); mask++){
int c = Integer.bitCount(mask);
//遍历n个数
for(int i = 0; i < n; i++){
//如果第i个数在nums2中被选择
if((mask & (1 << i)) > 0){
//mask ^ (1 << i),让mask的第i位变成0
dp[mask] = Math.min(dp[mask], dp[mask ^ (1 << i)] + (nums1[c - 1] ^ nums2[i]));
}
}
}
return dp[(1 << n) - 1];
}
}
这种题还要多练练
小结
这次比赛比上次有进步,尽管排名没有进步啊哈哈;但是三道题应该还是能做出来的,目标还是三道题,遇到代码多的要更加考虑好细节,加油!