数据挖掘之关联规则算法Apriori

关联规则最初是针对购物篮分析问题提出的，其目的是为了发现交易数据库中不同商品之间的关联规则。

关联规则挖掘的问题可以划分为两个子问题：

• 发现频繁项目集：通过用户给定Minsupport，寻找所有频繁项目集或者最大频繁项目集。
• 生成关联规则：通过用户给定Minconfidence，在频繁项目集中，寻找关联规则。

一些小概念

项目集的支持度

给定一个全局项目集I和数据库D，I中的一个项目集A在D上的支持度是指包含A的事务在D中所占的百分比。

频繁项目集

D中所有大于等于最小支持度Minsupport的项目集称频繁项目集。

关联规则和置信度

一个定义在I和D上的关联规则形如A=>B，它的置信度是指包含A和B的事务数与包含A的事务数之比。

强关联规则

D在I上满足最小支持度和最小置信度Minconfidence的关联规则称为强关联规则。

 Apriori算法

Apriori算法利用了Apriori性质，频繁项集的所有非空子集也必须是频繁的。

它通过逐层接待的方法，先找到频繁1项集L1，然后利用L1找到频繁2项集L2，接着用L2找L3，直到找不到频繁k项集，找每个Lk时候都需要一次数据库扫描。

案例演示（数据挖掘课程作业~

实验对象：实验对象为GNC订单明细表

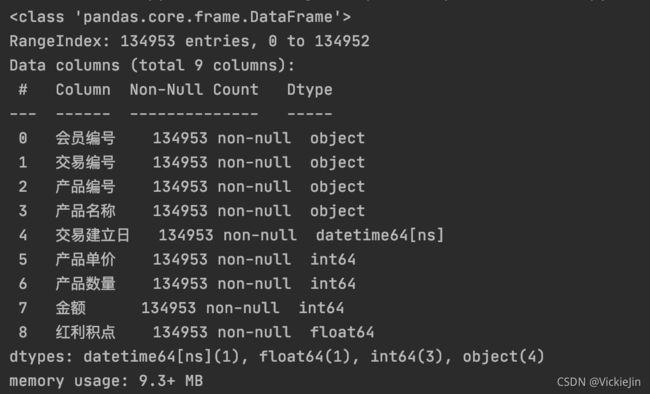
数据读取：首先通过read_excel读取数据，将文件转换为DataFrame格式。可以看到数据的列标签和每列的数据类型如图所示。

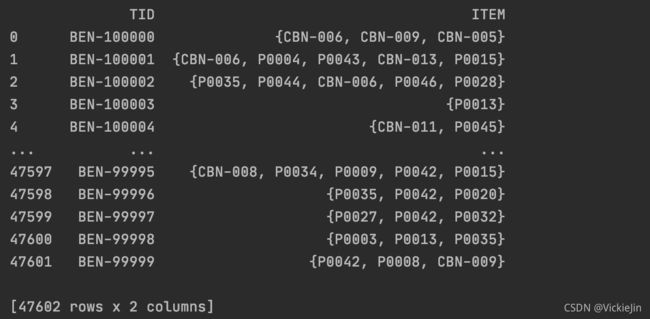
数据集处理：为了方便分析，这里提取交易编号和产品编号两列，并对其进行分组处理，得到新的数据集格式，用于下一步的关联分析的挖掘，处理后的数据集如图所示。

完整代码

# -*- coding: utf-8 -*-
import xlrd
import xlwt
from numpy import *
import pandas as pd

f1 = 'file1.xlsx'
f2 = 'apriori_rules.xls'
df = pd.read_excel(f1)
data = df.groupby('TID')['ITEM'].apply(set).reset_index()


a = data['ITEM'] #取列表数据


#获取候选1项集，dataSet为事务集。返回一个list，每个元素都是set集合
def createC1(dataSet):
    C1 = []   # 元素个数为1的项集（非频繁项集，因为还没有同最小支持度比较）
    for transaction in dataSet:
        for item in transaction:
            if not [item] in C1:
                C1.append([item])
    C1.sort()  # 这里排序是为了，生成新的候选集时可以直接认为两个n项候选集前面的部分相同
    # 因为除了候选1项集外其他的候选n项集都是以二维列表的形式存在，所以要将候选1项集的每一个元素都转化为一个单独的集合。
    # return C1
    # print(C1)
    return list(map(frozenset, C1))   #map(frozenset, C1)的语义是将C1由Python列表转换为不变集合（frozenset，Python中的数据结构）

# 找出候选集中的频繁项集
# dataSet为全部数据集，Ck为大小为k（包含k个元素）的候选项集，minSupport为设定的最小支持度
def scanD(dataSet, Ck, minSupport):
    ssCnt = {}   # 记录每个候选项的个数
    for tid in dataSet:
        for can in Ck:
            if can.issubset(tid):
                ssCnt[can] = ssCnt.get(can, 0) + 1   # 计算每一个项集出现的频率
    numItems = float(len(dataSet))
    retList = []
    supportData = {}
    for key in ssCnt:
        support = ssCnt[key] / numItems
        if support >= minSupport:
            retList.insert(0, key)  #将频繁项集插入返回列表的首部
        supportData[key] = support
    return retList, supportData   #retList为在Ck中找出的频繁项集（支持度大于minSupport的），supportData记录各频繁项集的支持度

# 通过频繁项集列表Lk和项集个数k生成候选项集C(k+1)。
def aprioriGen(Lk, k):
    # print('Lk:',Lk)
    retList = []
    lenLk = len(Lk)
    for i in range(lenLk):
        for j in range(i + 1, lenLk):
            # 前k-1项相同时，才将两个集合合并，合并后才能生成k+1项
            L1 = list(Lk[i])[:k-2]
            L2 = list(Lk[j])[:k-2]   # 取出两个集合的前k-1个元素
            L1.sort(); L2.sort()
            # print('L1,L2',L1,L2)
            if L1 == L2:
                retList.append(Lk[i] | Lk[j])
    # print(retList)
    return retList

# 获取事务集中的所有的频繁项集
# Ck表示项数为k的候选项集，最初的C1通过createC1()函数生成。Lk表示项数为k的频繁项集，supK为其支持度，Lk和supK由scanD()函数通过Ck计算而来。
def apriori(dataSet, minSupport=0.1):
    C1 = createC1(dataSet)  # 从事务集中获取候选1项集
    # print(C1)
    D = list(map(set, dataSet))  # 将事务集的每个元素转化为集合
    L1, supportData = scanD(D, C1, minSupport)  # 获取频繁1项集和对应的支持度
    L = [L1]  # L用来存储所有的频繁项集
    # 项集应该至少含有2个元素，所以 k=2
    k = 2
    while (len(L[k-2]) > 0): # 一直迭代到项集数目过大而在事务集中不存在这种n项集
        Ck = aprioriGen(L[k-2], k)   # 根据频繁项集生成新的候选项集。Ck表示项数为k的候选项集
        Lk, supK = scanD(D, Ck, minSupport)  # Lk表示项数为k的频繁项集，supK为其支持度
        # print(Lk)
        L.append(Lk)
        supportData.update(supK)  # 添加新频繁项集和他们的支持度
        k += 1         # 新生成的项集中的元素个数应不断增加
    # print(L, supportData)
    # print(L)
    return L, supportData


def generateRules(L, supportData, minConf=0.2):  #supportData is a dict coming from scanD
    bigRuleList = []
    for i in range(1, len(L)):#only get the sets with two or more items
        print('i:',i)
        for freqSet in L[i]:
            print('L[i]:',L[i])
            print('freqSet:',freqSet)
            H1 = [frozenset([item]) for item in freqSet]
            print('H1:',H1)
            if (i > 1):
                rulesFromConseq(freqSet, H1, supportData, bigRuleList, minConf)
            else:
                calcConf(freqSet, H1, supportData, bigRuleList, minConf)
    return bigRuleList

def calcConf(freqSet, H, supportData, brl, minConf=0.2):
    prunedH = [] #create new list to return
    for conseq in H:
        print('conseq:',conseq)
        print('freqSet-conseq:',freqSet-conseq)
        conf = supportData[freqSet]/supportData[freqSet-conseq] #calc confidence
        if conf >= minConf:
            print(freqSet-conseq,'-->',conseq,'conf:',conf)
            brl.append((freqSet-conseq, conseq, conf))
            prunedH.append(conseq)
#     print 'prunedH:',prunedH
    return prunedH

#rulesFromConseq目的就是对每一个频繁项集生成右边的规则，一个频繁项集可以生成很多右边的规则
#if (len(freqSet) > (m + 1))这是迭代停止的条件，也就是当右边的规则的元素数+1=该频繁项长度时停止迭代
#if (len(Hmp1) > 1)当Hmp1的长度大于1时才能合并，合并需要至少两个frozenset
def rulesFromConseq(freqSet, H, supportData, brl, minConf=0.2):
    m = len(H[0])
    print('m:', m)
    print('len(freqSet):', len(freqSet))
    if (len(freqSet) > (m + 1)): #try further merging
        Hmp1 = aprioriGen(H, m+1)#create Hm+1 new candidates
        print('Hmp1:',Hmp1)
        Hmp1 = calcConf(freqSet, Hmp1, supportData, brl, minConf)
        print('Hmp2:',Hmp1)
        if (len(Hmp1) > 1):    #need at least two sets to merge
            print('---------')
            rulesFromConseq(freqSet, Hmp1, supportData, brl, minConf)
            print('*********')






dataSet = a  # 获取事务集。每个元素都是列表
# C1 = createC1(dataSet)  # 获取候选1项集。每个元素都是集合
# D = list(map(set, dataSet))  # 转化事务集的形式，每个元素都转化为集合。
# # retList, suppDat = scanD(D, C1, 0.1)
L, suppData = apriori(dataSet, minSupport=0.03)
generateRules(L,suppData,minConf=0.2)

 数据集见：https://download.csdn.net/download/sinat_34376453/22035783