【手撕算法】【Apriori】关联规则Apriori原理、代码实现

1.前言

⭐️ 开箱即食，直接复制，懒人传送门：4.1懒人必备，开箱速食

⭐️ 本文主要从原理、代码实现 理论和实战两个角度来剖析Apriori算法

⭐️ 理论部分主要是关于 什么是 频繁项集、支持度、置信度

⭐️ 懒得写代码的，可以直接跳的第五节，直接安装依赖包：5.懒人必备，开箱速食

2.简介

⭐️ 关联规则挖掘算法通常是无监督学习，通过分析数据集，挖掘出潜在的关联规则，最典型的一个例子是啤酒与尿不湿的故事

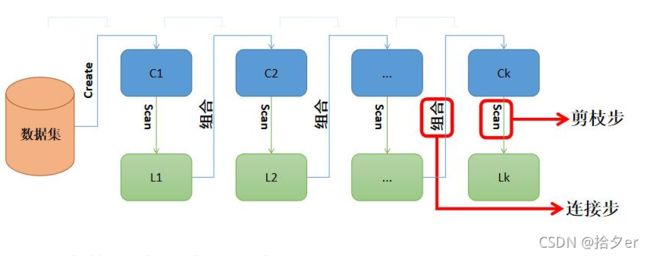
⭐️ Apriori 是第一个关联规则挖掘算法，也是最经典的算法，它利用逐层搜索的迭代方法找出数据库中项集的关系，以形成规则，其过程由连接（类矩阵运算）与剪枝（去掉那些没必要的中间结果）组成。

⭐️ 该算法既可以发现频繁项集，又可以挖掘物品（项）之间的关联规则。

⭐️ 该算法采用支持度来量化频繁项集，采用置信度来量化关联规则

3.原理

3.0.示例

我们使用如下交易表格来用嘴来仿真我们的Apriori算法的工作步骤，以及介绍他们的概念和原理

交易记录如下：

交易ID	商品列表
1	土豆，尿不湿，啤酒
2	巧克力，牛奶，土豆，啤酒
3	牛奶，尿不湿，啤酒
4	巧克力，尿不湿，啤酒
5	巧克力，啤酒

3.1.概念介绍

⭐️ 支持度： $P(A\cap B)$，表示既有A又有B的概率。例如，我们总共有5个交易订单，其中同时有啤酒 和 尿不湿的总共有3单，那么 $P(A\cap B)=3/5=0.6$，即支持度为0.6

⭐️ 置信度： $P(B|A)$，表示在A发生的事件中同时发生B的概率 $P(AB)/P(A)$, 他表现的是AB两个事件的相关程度，准确来说是A对B的关联程度，注意并非是B对A的关联程度。例如，我们总共有5个交易订单，其中同时有啤酒 和 尿不湿 的总共有3单， 即$P(AB)=3/5=0.6$，我们含有啤酒的订单有5个交易单，则$P(A)=5/5=1.0$含有尿不湿的为3单，则$P(B)=3/5=0.6$，那么啤酒对尿不湿的关联程度为：$P(B|A)=P(AB)/P(A)=0.6/1.0=0.6$，尿不湿对啤酒的关联程度为：$P(A|B)=P(AB)/P(B)=0.6/0.6=1.0$

⭐️ 频繁k项集： 项集即为项的集合，项可以是商品，那么项集就是商品的集合，频繁项集就是经常（满足最小支持度）在一起的物品的集合，例如尿不湿和啤酒，称之为频繁2项集

3.2.Apriori原理

⭐️ 如果某个项集是频繁的，那么他的所有子集也是频繁的，例如：如果最小支持度为0.5，那么啤酒和尿不湿的支持度为0.6，那么他的子集，啤酒和尿不湿的支持度分别为$1.0$和$0.6$

⭐️ 如果某个项集是非频繁的，那么他的所有超集也是非频繁的，例如：如果最小支持度为0.5，牛奶只有两单，两单分别是和啤酒、尿不湿一起购买。那么牛奶的支持度为$2/5=0.4$，其是小于最小支持度的，所以其是非频繁的。而他们的超集为{啤酒, 牛奶} 和 {尿不湿, 牛奶}。他们的支持度分别为 $2/5=0.4$ 和 $1/5=0.2$， 所以他们都是非频繁的，即牛奶的超集是非频繁的。

3.3.优点

⭐️ 该算法的关联规则关联规则是在频繁项集基础上产生的，这可以保证这些规则的支持度达到指定的水平，具有普遍性和令人信服的水平

⭐️ 算法简单，易于理解，对数据的要求低

3.4.缺点

⭐️ 在每一步产生候选项目集的时候循环产生的组合过多，项数越多，越消耗计算资源，如果不剪枝，其时间复杂度为$O(2^n)$，n为项集个数。假如我们有6个项，有6种类型组合方式（单个组合，两两组合，三三组合等），其数学公式为： $C_6^1+C_6^2+C_6^3+C_6^4+C_6^5+C_6^6=2^6-1$

⭐️ 每次计算项集的支持度的时候，都对数据库中的全部数据进行了一遍扫描比较，I/O负载很大。

3.5.算法步骤

⭐️ 我们使用以下步骤来说明我们的算法

第一步：输入数据集X，对应我们的示例为五个交易记录
第二步：确定数据集X中所包含的项集，不重复，对应我们的示例则为{牛奶，巧克力，尿不湿，啤酒，土豆}
第三步：进行第一次迭代，把每个项集中的项目单独扫描统计（即某个项在多少个交易记录中出现了），将每个项都作
		为候选 1 项集 C1 的成员，并计算每个项的支持度
第四步：设定最小支持度，根据候选 1 项集C1的成员，对比其支持度和最小支持度，大于等于最小支持度的为候选 2 
		项集 C2。
第五步：保持最小支持度不变，重复进行第四部，直到没有满足最小支持度的项集，此时输出最终频繁项集。
第六步：设定最小置信度，根据 k 项集CK 和 k+1项集Ck+1，计算k项集的置信度，满足最小置信度的则筛选存储。
第七步：重复第六步，k值从1开始，直到到最大值，返回具有强相关的关联规则列表。

⭐️ 借用俩图说明我们第1~5步

---

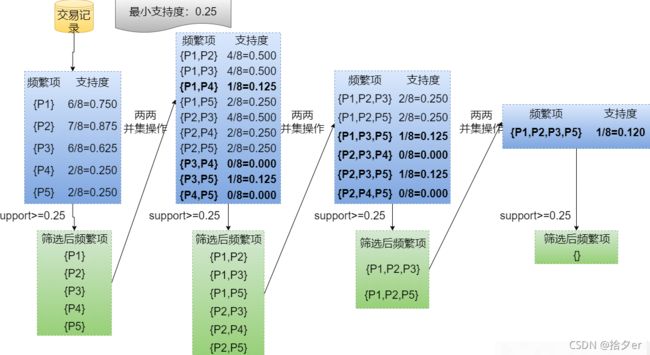
-----------------------以下是我们根据3.0的示例部分进行算法工作步骤的说明----------------------------------

⭐️ 准备数据：数据库中的交易数据

交易ID	商品列表
1	土豆，尿不湿，啤酒
2	巧克力，牛奶，土豆，啤酒
3	牛奶，尿不湿，啤酒
4	巧克力，尿不湿，啤酒
5	巧克力，啤酒

---

⭐️ 第一轮：先从数据库中扫描，生成 1 项集 C1

项集	支持度
{土豆}	0.40
{尿不湿}	0.60
{啤酒}	1.00
{牛奶}	0.40
{巧克力}	0.60

⭐️ 第一轮：调用Scan函数，过滤支持度小于0.5的项集，得到频繁 1 项集 L1

项集	支持度
{尿不湿}	0.60
{啤酒}	1.00
{巧克力}	0.60

---

⭐️ 第二轮：根据 频繁 1 项集 L1，生成 2 项集 C2

项集	支持度
{尿不湿，啤酒}	0.60
{巧克力，啤酒}	0.60
{巧克力，尿不湿}	0.20

⭐️ 第二轮：调用Scan函数，过滤支持度小于0.5的项集，得到频繁 2 项集 L2

项集	支持度
{尿不湿，啤酒}	0.60
{巧克力，啤酒}	0.60

---

⭐️ 第三轮：根据 频繁 2 项集 L2，生成 3 项集 C3

项集	支持度
{尿不湿，啤酒，巧克力}	0.20

⭐️ 第三轮：调用Scan函数，过滤支持度小于0.5的项集，得到频繁 3 项集 L3 因为L3为空，所以算法到这里结束

项集	支持度
{None}	None

---

-------------------------------我们采用以下步骤挖掘我们的强关联规则---------------------------------------

⭐️ 第一步：获取所有挖掘出来的规则

规则	置信度
{啤酒} -----> { 尿不湿}	0.60
{巧克力} -----> { 尿不湿}	0.33
{尿不湿} -----> {啤酒 }	1.00
{巧克力} -----> { 啤酒}	1.00
{尿不湿，啤酒} -----> {巧克力 }	0.33
{巧克力，啤酒} -----> {尿不湿}	0.33

⭐️ 第二步：过滤置信度小于0.7的规则，生成强规则

规则	置信度
{尿不湿} -----> {啤酒 }	1.00
{巧克力} -----> { 啤酒}	1.00

至此，我们得到了我们的了我们的两个强规则，即当我们买尿不湿的时候，有100%的概率会买啤酒；买巧克力的时候，有100%的概率会买啤酒

---

4.代码实现

4.1懒人必备，开箱速食

⭐️ 此代码已经验证通过运行，点击代码框的右上角即可复制全部代码

#1.构建候选1项集C1
def createC1(dataSet):
    c1 =list(set([y for x in dataSet for y in x]))
    c1.sort()
    c2 = [[x] for x in c1]
    return list(map(frozenset, c2))

#将候选集Ck转换为频繁项集Lk
#D：原始数据集
#Cn: 候选集项Ck
#minSupport:支持度的最小值
def scanD(D, Ck, minSupport):
    #候选集计数
    ssCnt = {}
    for tid in D:
        for can in Ck:
            if can.issubset(tid):
                if can not in ssCnt.keys(): ssCnt[can] = 1
                else: ssCnt[can] += 1

    numItems = float(len(D))
    Lk= []     # 候选集项Cn生成的频繁项集Lk
    supportData = {}    #候选集项Cn的支持度字典

    #计算候选项集的支持度, supportData key:候选项， value:支持度
    for key in ssCnt:
        support = ssCnt[key] / numItems
        if support >= minSupport:
            Lk.append(key)
        supportData[key] = support
    return Lk, supportData

#连接操作，将频繁Lk-1项集通过拼接转换为候选k项集
def aprioriGen(Lk_1, k):
    Ck = []
    lenLk = len(Lk_1)
    for i in range(lenLk):
        L1_list = list(Lk_1[i])
        L1 = L1_list[:k - 2]
        L1.sort()
        for j in range(i + 1, lenLk):
            #前k-2个项相同时，将两个集合合并
            L2_list = list(Lk_1[j])
            L2 = list(Lk_1[j])[:k - 2]
            L2.sort()
            if L1 == L2:
                Ck.append(Lk_1[i] | Lk_1[j])
    return Ck

def apriori(dataSet, minSupport = 0.5):
    C1 = createC1(dataSet)
    L1, supportData = scanD(dataSet, C1, minSupport)
    L = [L1]
    k = 2
    while (len(L[k-2]) > 0):
        Lk_1 = L[k-2]
        Ck = aprioriGen(Lk_1, k)
        print("ck:",Ck)
        Lk, supK = scanD(dataSet, Ck, minSupport)
        supportData.update(supK)
        print("lk:", Lk)
        L.append(Lk)
        k += 1
    return L, supportData

#生成关联规则
#L: 频繁项集列表
#supportData: 包含频繁项集支持数据的字典
#minConf 最小置信度
def generateRules(L, supportData, minConf=0.7):
    #包含置信度的规则列表
    bigRuleList = []
    #从频繁二项集开始遍历
    for i in range(1, len(L)):
        for freqSet in L[i]: 
            H1 = [frozenset([item]) for item in freqSet] # 拆分项集
            if (i > 1):
                rulesFromConseq(freqSet, H1, supportData, bigRuleList, minConf)
            else:
                calcConf(freqSet, H1, supportData, bigRuleList, minConf)
    return bigRuleList


# 计算是否满足最小可信度
def calcConf(freqSet, H, supportData, brl, minConf=0.7):
    prunedH = []
    #用每个conseq作为后件
    for conseq in H:
        # 计算置信度
        P_A = supportData[freqSet.difference(conseq)]
        conf = supportData[freqSet] / P_A
        if conf >= minConf:
            print(freqSet - conseq, '-->', conseq, 'conf:', conf)
            # 元组中的三个元素：前件、后件、置信度
            brl.append((freqSet - conseq, conseq, conf))
            prunedH.append(conseq)
    #返回后件列表
    return prunedH


# 对规则进行评估
def rulesFromConseq(freqSet, H, supportData, brl, minConf=0.7):
    m = len(H[0])
    if (len(freqSet) > (m + 1)):
        Hmp1 = aprioriGen(H, m + 1)
       # print(1,H, Hmp1)
        Hmp1 = calcConf(freqSet, Hmp1, supportData, brl, minConf)
        if (len(Hmp1) > 0):
            rulesFromConseq(freqSet, Hmp1, supportData, brl, minConf)

dataset = [['土豆', '尿不湿', '啤酒'], ['巧克力', '牛奶', '土豆', '啤酒'] , ['牛奶', '尿不湿', '啤酒'], \
                ['巧克力', '尿不湿', '啤酒'], ['巧克力', '啤酒']]
L, supportData = apriori(dataset, minSupport=0.5)
rules = generateRules(L, supportData, minConf=0.7)
for e in rules:
    print(e)

4.2.代码详解

⭐️ createC1(dataSet): 扫描所有的事件（交易），获取所有项（商品）的集合。

#1.构建候选1项集C1
def createC1(dataSet):
    c1 =list(set([y for x in dataSet for y in x]))
    c1.sort()
    c2 = [[x] for x in c1]
    return list(map(frozenset, c2))

⭐️ scanD(D, Ck, minSupport): 根据最小支持度，从候选项集Ck里筛选出符合最小支持度的频繁项集Lk

#将候选集Ck转换为频繁项集Lk
#D：原始数据集
#Cn: 候选集项Ck
#minSupport:支持度的最小值
def scanD(D, Ck, minSupport):
    #候选集计数
    ssCnt = {}
    for tid in D:
        for can in Ck:
            if can.issubset(tid):
                if can not in ssCnt.keys(): ssCnt[can] = 1
                else: ssCnt[can] += 1

    numItems = float(len(D))
    Lk= []     # 候选集项Cn生成的频繁项集Lk
    supportData = {}    #候选集项Cn的支持度字典
    #计算候选项集的支持度, supportData key:候选项， value:支持度
    for key in ssCnt:
        support = ssCnt[key] / numItems
        if support >= minSupport:
            Lk.append(key)
        supportData[key] = support
    return Lk, supportData

⭐️ aprioriGen(Lk_1, k): 将频繁项集Lk-1，通过拼接得到候选Ck项集，以便scanD(D, Ck, minSupport): 这一函数用来生成频繁项集Lk

#连接操作，将频繁Lk-1项集通过拼接转换为候选k项集
def aprioriGen(Lk_1, k):
    Ck = []
    lenLk = len(Lk_1)
    for i in range(lenLk):
        L1_list = list(Lk_1[i])
        L1 = L1_list[:k - 2]
        L1.sort()
        for j in range(i + 1, lenLk):
            #前k-2个项相同时，将两个集合合并
            L2_list = list(Lk_1[j])
            L2 = list(Lk_1[j])[:k - 2]
            L2.sort()
            if L1 == L2:
                Ck.append(Lk_1[i] | Lk_1[j])
    return Ck

⭐️ apriori(dataSet, minSupport = 0.5): 获取并保存每一级的的频繁项集L，以便后来用来计算，指定频繁项的置信度

# 获取并保存每一级的的频繁项集L
def apriori(dataSet, minSupport = 0.5):
    C1 = createC1(dataSet)
    L1, supportData = scanD(dataSet, C1, minSupport)
    L = [L1]
    k = 2
    while (len(L[k-2]) > 0):
        Lk_1 = L[k-2]
        Ck = aprioriGen(Lk_1, k)
        # print("ck:",Ck)
        Lk, supK = scanD(dataSet, Ck, minSupport)
        supportData.update(supK)
        # print("lk:", Lk)
        L.append(Lk)
        k += 1
    return L, supportData

⭐️ generateRules(L, supportData, minConf=0.7): 根据频繁项集L和最小置信度生成强关联规则

#生成关联规则
#L: 频繁项集列表
#supportData: 包含频繁项集支持数据的字典
#minConf 最小置信度
def generateRules(L, supportData, minConf=0.7):
    #包含置信度的规则列表
    bigRuleList = []
    #从频繁二项集开始遍历
    for i in range(1, len(L)):
        for freqSet in L[i]: 
            H1 = [frozenset([item]) for item in freqSet] # 拆分项集
            if (i > 1):
                rulesFromConseq(freqSet, H1, supportData, bigRuleList, minConf)
            else:
                calcConf(freqSet, H1, supportData, bigRuleList, minConf)
    return bigRuleList

⭐️ calcConf(freqSet, H, supportData, brl, minConf=0.7): 用来进行剪枝操作，计算是否满足最小置信度

# 计算是否满足最小可信度
def calcConf(freqSet, H, supportData, brl, minConf=0.7):
    prunedH = []
    #用每个conseq作为后件
    for conseq in H:
        # 计算置信度
        P_A = supportData[freqSet.difference(conseq)]
        conf = supportData[freqSet] / P_A
        if conf >= minConf:
            print(freqSet - conseq, '-->', conseq, 'conf:', conf)
            # 元组中的三个元素：前件、后件、置信度
            brl.append((freqSet - conseq, conseq, conf))
            prunedH.append(conseq)
    #返回后件列表
    return prunedH

⭐️ rulesFromConseq(freqSet, H, supportData, brl, minConf=0.7): 用来获取所有满足最小置信度的强关联规则，也就是返回挖掘出来的所有强关联规则

def rulesFromConseq(freqSet, H, supportData, brl, minConf=0.7):
    m = len(H[0])
    if (len(freqSet) > (m + 1)):
        Hmp1 = aprioriGen(H, m + 1)
       # print(1,H, Hmp1)
        Hmp1 = calcConf(freqSet, Hmp1, supportData, brl, minConf)
        if (len(Hmp1) > 0):
            rulesFromConseq(freqSet, Hmp1, supportData, brl, minConf)

5.总结

⭐️ 自己写了半天，发现有现成的别人写好的包，直接掉包就可以了，代码如下：

# 安装：pip install efficient-apriori
from efficient_apriori import apriori
freqItemSet, rules = apriori(dataset, 0.5, 0.7)
print(rules)

⭐️ Apriori算法效率比较低，建议在使用的时候直接使用基于Apriori算法开发的FP-growth算法，由于其是树形数据结构，所以其效率很高，可以通过以下依赖包实现：fpgrowth_py 实现代码如下：

# 安装：pip install fpgrowth_py
from fpgrowth_py import fpgrowth
dataset = [[1, 3, 4], [2, 3, 5], [1, 2, 3, 5], [2, 5]]
freqItemSet, rules = fpgrowth(dataset, 0.5, 0.7)
print(rules) 

6.参考资料

百度百科：APRIORI
知乎：数据挖掘十大算法—— Apriori
CSDN：Apriori算法–关联分析算法（一）
efficient-apriori 2.0.1
fpgrowth-py 1.0.0