力扣337.打家劫舍3（树形dp)

题目描述：

小偷又发现了一个新的可行窃的地区。这个地区只有一个入口，我们称之为 root 。

除了 root 之外，每栋房子有且只有一个“父“房子与之相连。一番侦察之后，聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ，房屋将自动报警。

给定二叉树的 root 。返回 在不触动警报的情况下 ，小偷能够盗取的最高金额 。

示例 1:

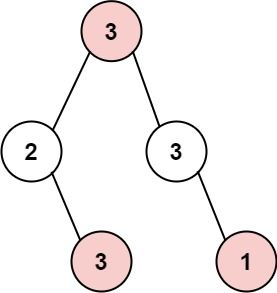
输入: root = [3,2,3,null,3,null,1]
输出: 7 
解释: 小偷一晚能够盗取的最高金额 3 + 3 + 1 = 7

示例 2:

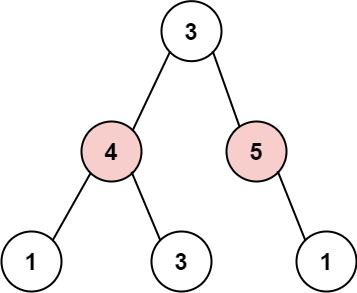
输入: root = [3,4,5,1,3,null,1]
输出: 9
解释: 小偷一晚能够盗取的最高金额 4 + 5 = 9

提示：

• 树的节点数在 [1, 104] 范围内
• 0 <= Node.val <= 104

思路：

这道题呢换汤不换药，其实就是把之前的线性结构变成了树形，还是不能找相邻的房子，解法还是动态规划，只不过在树上做而已。（二叉树）

这里给出的数据结构是 TreeNode root

给出此结构的用法：

1.root->left 左节点的值

2.root->right 右节点的值

3.root->val 根节点的值

每一个房子都是一个节点，我们从整个树的根节点root依次往下看，对于每一个节点都有两种选择：

1.选这个房子，那么我们就不能选这个房子的左右节点，也就是题目给的相邻的房子。

2.不选这个房子，那么我们可以同时选其左右节点的房子。

我们用哈希表来映射根节点与当前这个节点可以偷的最大的钱的数量。

因为每个节点都有选和不选两种状态，那么我们就分别表示：

unordered_map f,g;

f[node]表示选这个节点的能最多偷多少钱

g[node] 表示不选这个节点最多能投多少钱

所以最后的答案就是max(f[root],g[root])

状态转移方程：

1.选当前节点，意味着左右节点不能选,为什么是相加呢？因为要想完整的表达出f[node]这个状态，就需要把这个状态里的所有子状态结合起来，这样才能 ”不漏“：

 f[node]=node->val+g[node->left]+g[node->right]

2.不选当前节点，意味着左右节点都能选，这里的能，并不意味着一定，我们要看选了这个节点与不选这个节点哪个对答案的贡献更大，也就是值更大：

g[node]=max(f[node->left],g[node->left])+max(f[node->right],g[node->right])

代码：

class Solution {
public:
    unordered_map f, g;//f表示拿节点的，g表示不拿节点的可以偷的最多的钱

    void dfs(TreeNode* node) {
        if (!node) {
            return;
        }

        dfs(node->left);
        dfs(node->right);
        f[node] = node->val + g[node->left] + g[node->right];
        g[node] = max(f[node->left], g[node->left]) + max(f[node->right], g[node->right]);
    }
    int rob(TreeNode* root) {
        dfs(root);

        return max(g[root], f[root]);
    }
};

这道题其实就是树形dp的板子题，有兴趣的可以去看看上司的舞会这道题，可能容易理解一点。