数据结构-树(二叉树,二分搜索树,堆,线段树,并查集,平衡二叉树,二三树,红黑树)原理与代码实战
树
本文涉及的完整代码在文章尾部可以获取
一:基本介绍
为什么要用树?
打个比方,我们有很多文件,都罗列在桌面,很难寻找。而对文件夹分类,就会很容易找到结果。
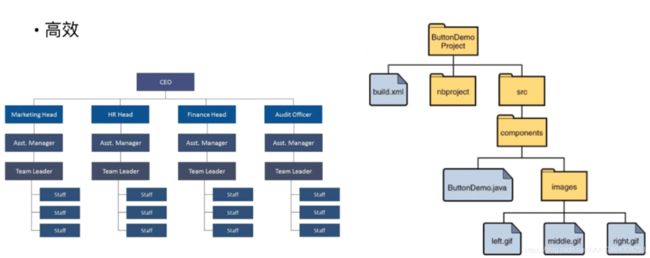
定义
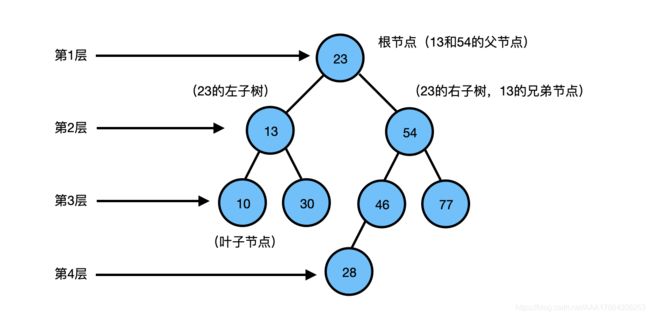
- 根节点:一棵树最上面的节点称为根节点。
- 父节点、子节点:如果一个节点下面连接多个节点,那么该节点称为父节点,它下面的节点称为子 节点。
- 叶子节点:没有任何子节点的节点称为叶子节点。
- 兄弟节点:具有相同父节点的节点互称为兄弟节点。
- 节点度:节点拥有的子树数。上图中,13的度为2,46的度为1,28的度为0。
- 树的深度:从根节点开始(其深度为0)自顶向下逐层累加的。上图中,13的深度是1,30的深度是2,28的深度是3。
- 树的高度:从叶子节点开始(其高度为0)自底向上逐层累加的。54的高度是2,根节点23的高度是3。
二:二叉树与二分搜索树
二叉树
二叉树定义:二叉树是每个节点最多有两个子树的树结构。
二叉树几个基本概念
- 满二叉树:如果一棵二叉树只有度为0的结点和度为2的结点,并且度为0的结点在同一层上,则这棵二叉树为满二叉树
- 完全二叉树:若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。
几个特征: - 叶子节点不一定都在底层
- 二叉树具有唯一根节点
- 每个节点最多有两个孩子
- 每个节点最多有一个父亲
- 二叉树不一定是满的
- NULL也是二叉树
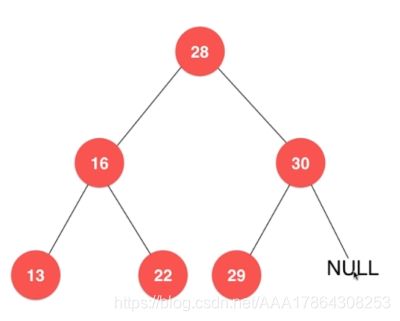
二叉树
public class BT {
// 节点
private class Node {
E e;
Node left, right;
public Node(E e) {
this.e = e;
left = null;
right = null;
}
}
}
二分搜索树
二分搜索树除了满足二叉树外还满足左子树大于父点的值,右子树大于父点的值。

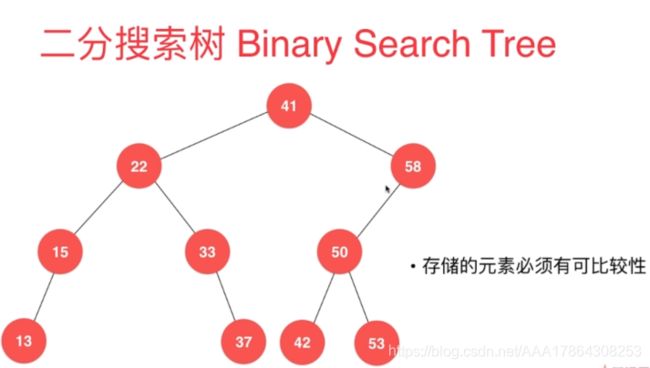
引用二分搜索树目的:大大加快查询速度。前提:保证可比性。
定义
public class BST<E extends Comparable<E>> {
// 02 节点
private class Node {
// 03 成员变量
E e;
// 04 左孩子右孩子
Node left, right;
public Node(E e) {
this.e = e;
left = null;
right = null;
}
}
/**
* 05 根节点
*/
private Node root;
/**
* 06 存储了多少元素
*/
private int size;
public BST() {
root = null;
size = 0;
}
public int size() {
return size;
}
public boolean isEmpty() {
return size == 0;
}
}
插入
向二分搜索树依次添加[20,10,6,14,29,25,33]7个元素。看一下这个添加的过程。
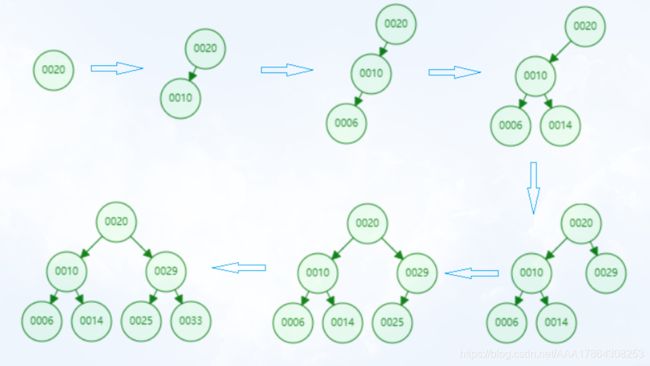
插入方法一
/**
* 向二分搜索树中添加新的元素e
*
* @param e
*/
public void add(E e) {
/**
* 插入根节点
*/
if (root == null) {
root = new Node(e);
size++;
} else {
add(root, e);
}
}
/**
* 向以node为根的二分搜索树中插入元素e,递归算法
*
* @param node
* @param e
*/
private void add(Node node, E e) {
/**
* 左(右)子树为空
*/
if (e.equals(node.e)) {
return;
} else if (e.compareTo(node.e) < 0 && node.left == null) {
node.left = new Node(e);
size++;
return;
} else if (e.compareTo(node.e) > 0 && node.right == null) {
node.right = new Node(e);
size++;
return;
}
/**
* 左(右)不为空
*/
if (e.compareTo(node.e) < 0) {
// 以左子树为第一个参数 add
add(node.left, e);
} else {
// 以右子树为第一个参数 add
add(node.right, e);
}
}
此方法非常臃肿,没有递归到底
插入方法二(返回插入后的节点)
// 向二分搜索树中添加新的元素e
public void add(E e) {
root = add(root, e);
}
/**
* 向以node为根的二分搜索树中插入元素e,递归算法
* 返回插入新节点后二分搜索树的根
*
* @param node
* @param e
* @return
*/
private Node add(Node node, E e) {
if (node == null) {
size++;
return new Node(e);
}
if (e.compareTo(node.e) < 0) {
node.left = add(node.left, e);
} else if (e.compareTo(node.e) > 0) {
node.right = add(node.right, e);
}
return node;
}
遍历
深度优先遍历-递归:前序遍历
遍历顺序:父节点,左子树,右子树
/
// 5 //
// / \ //
// 3 6 //
// / \ \ //
// 2 4 8 //
/
5 3 2 4 6 8
// 前序遍历以node为根的二分搜索树, 递归算法
private void preOrder(Node node) {
if (node == null) {
return;
}
System.out.println(node.e);
preOrder(node.left);
preOrder(node.right);
}
深度优先遍历-递归:中序遍历
遍历顺序:左子树,父节点,右子树,有序
/
// 5 //
// / \ //
// 3 6 //
// / \ \ //
// 2 4 8 //
/
2 3 4 5 6 8
private void inOrder(Node node) {
if (node == null) {
return;
}
inOrder(node.left);
System.out.println(node.e);
inOrder(node.right);
}
深度优先遍历-递归:后续遍历
遍历顺序:左子树,右子树,父节点
/
// 5 //
// / \ //
// 3 6 //
// / \ \ //
// 2 4 8 //
/
2 4 3 8 6 5
private void postOrder(Node node) {
if (node == null) {
return;
}
postOrder(node.left);
postOrder(node.right);
System.out.println(node.e);
}
深度优先遍历:非递归
非递归前序:自己的栈模拟系统栈
初始:根节点5入栈
栈顶5出栈,两个孩纸(6,3)入栈
栈顶3出栈,两个孩纸(4,2)入栈
// 二分搜索树的非递归前序遍历
/// // 5
// 5 // //
// / \ // //
// 3 6 // //
// / \ \ // 3 //
// 2 4 8 // 6 //
//
5 3 2 4 6 8
public void preOrderNR() {
if (root == null) {
return;
}
Stack<Node> stack = new Stack<Node>();
stack.push(root);
while (!stack.isEmpty()) {
Node cur = stack.pop();
System.out.println(cur.e);
if (cur.right != null) {
stack.push(cur.right);
}
if (cur.left != null) {
stack.push(cur.left);
}
}
}
层序遍历
初始:根节点5入栈
5出队,3,6入队
3出队,2,3入队
/ 3 // 5
// 5 // 6 //
// / \ // //
// 3 6 // //
// / \ \ // //
// 2 4 8 // //
/ //
5 3 6 2 4 8
// 二分搜索树的层序遍历
public void levelOrder() {
if (root == null) {
return;
}
Queue<Node> q = new LinkedList<Node>();
q.add(root);
while (!q.isEmpty()) {
Node cur = q.remove();
System.out.println(cur.e);
if (cur.left != null) {
q.add(cur.left);
}
if (cur.right != null) {
q.add(cur.right);
}
}
}
刪除
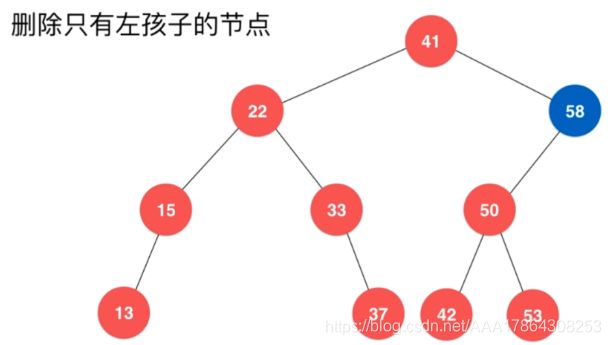
删除只有左孩子,或只有右孩子
删除有两个孩子
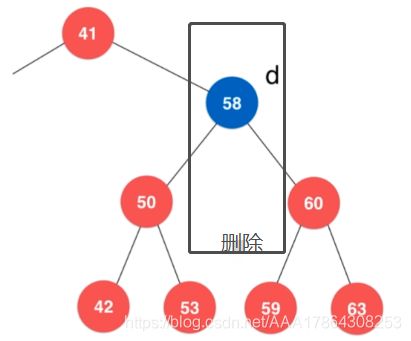
1962年计算机科学家Hibbard Deletion提出
找58的后继节点
找右子树的最小值
58右子树最小值为59

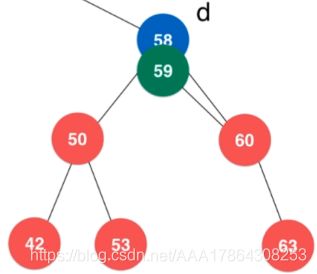
// 删除掉以node为根的二分搜索树中值为e的节点, 递归算法
// 返回删除节点后新的二分搜索树的根
private Node remove(Node node, E e) {
if (node == null) {
return null;
}
// 找到待删除元素
if (e.compareTo(node.e) < 0) {
node.left = remove(node.left, e);
return node;
} else if (e.compareTo(node.e) > 0) {
node.right = remove(node.right, e);
return node;
}
// 寻找成功
else {
// 待删除节点左子树为空的情况
if (node.left == null) {
Node rightNode = node.right;
node.right = null;
size--;
return rightNode;
}
// 待删除节点右子树为空的情况
if (node.right == null) {
Node leftNode = node.left;
node.left = null;
size--;
return leftNode;
}
// 待删除节点左右子树均不为空的情况
// 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
// 用这个节点顶替待删除节点的位置
Node successor = minimum(node.right);
successor.right = removeMin(node.right);
successor.left = node.left;
node.left = node.right = null;
return successor;
}
}
// 返回以node为根的二分搜索树的最小值所在的节点
private Node minimum(Node node) {
if (node.left == null) {
return node;
}
return minimum(node.left);
}
// 删除掉以node为根的二分搜索树中的最小节点
// 返回删除节点后新的二分搜索树的根
private Node removeMin(Node node) {
if (node.left == null) {
Node rightNode = node.right;
node.right = null;
size--;
return rightNode;
}
node.left = removeMin(node.left);
return node;
}
公众号内回复“树”即可获取完整的代码
更多前沿技术,面试技巧,内推信息请扫码关注公众号“云计算平台技术”
![]()
三:堆
二叉堆
最大堆:所有节点值都大于等于孩子节点值
最小堆:所有节点值都小于等于孩子节点值
结构表示:除类似BST外,完全二叉树可以用数组表示
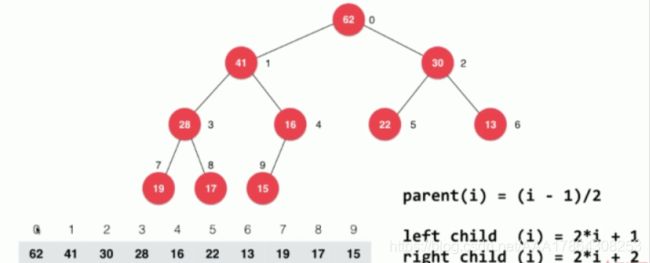
初始化
public class MaxHeap<E extends Comparable<E>> {
private Array<E> data;
public MaxHeap(int capacity) {
data = new Array<>(capacity);
}
public MaxHeap() {
data = new Array<>();
}
// 返回堆中的元素个数
public int size() {
return data.getSize();
}
// 返回一个布尔值, 表示堆中是否为空
public boolean isEmpty() {
return data.isEmpty();
}
// 返回完全二叉树的数组表示中,一个索引所表示的元素的父亲节点的索引
private int parent(int index) {
if (index == 0) {
throw new IllegalArgumentException("index-0 doesn't have parent.");
}
return (index - 1) / 2;
}
// 返回完全二叉树的数组表示中,一个索引所表示的元素的左孩子节点的索引
private int leftChild(int index) {
return index * 2 + 1;
}
// 返回完全二叉树的数组表示中,一个索引所表示的元素的右孩子节点的索引
private int rightChild(int index) {
return index * 2 + 2;
}
}
添加元素SIFT-UP
52找父亲节点41,不符合,交换

52找父亲节点62,符合,不交换

// 向堆中添加元素
public void add(E e) {
data.addLast(e);
siftUp(data.getSize() - 1);
}
// 向所有元素后添加一个新元素
public void addLast(E e){
add(size, e);
}
/**
* 上浮操作
*
* @param k
*/
private void siftUp(int k) {
while (k > 0 && data.get(parent(k)).compareTo(data.get(k)) < 0) {
data.swap(k, parent(k));
k = parent(k);
}
}
// 在index索引的位置插入一个新元素e
public void add(int index, E e){
if(index < 0 || index > size)
throw new IllegalArgumentException("Add failed. Require index >= 0 and index <= size.");
if(size == data.length)
resize(2 * data.length);
for(int i = size - 1; i >= index ; i --)
data[i + 1] = data[i];
data[index] = e;
size ++;
}
取出元素SIFT-DOWN
性质:只能取出最大元素
直接删除62不好融合,用16替换

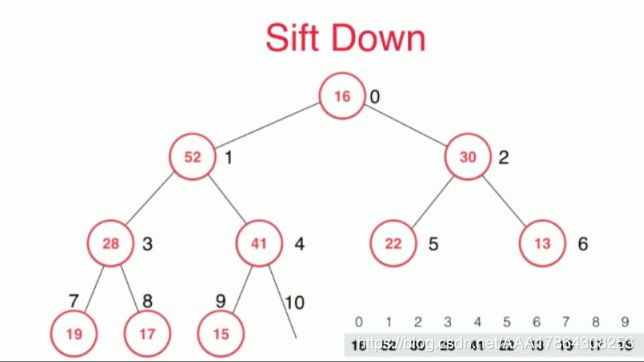
16选择孩子最大的元素52,如果比自己大,交换位置

16选择孩子最大的元素42,如果比自己大,交换位置
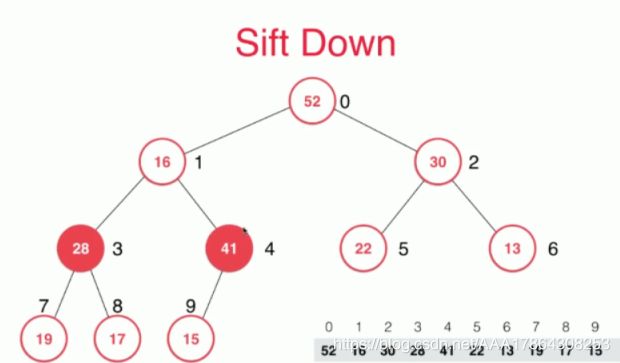
16选择孩子最大的元素15,如果比自己大,交换位置

/**
* 取出堆中最大元素
*
* @return
*/
public E extractMax() {
E ret = findMax();
data.swap(0, data.getSize() - 1);
data.removeLast();
siftDown(0);
return ret;
}
private void siftDown(int k) {
// 找到叶子节点
while (leftChild(k) < data.getSize()) {
int leftIndex = leftChild(k); // 在此轮循环中,data[k]和data[j]交换位置
// 获得比较大的孩子索引
if (leftIndex + 1 < data.getSize() &&
data.get(leftIndex + 1).compareTo(data.get(leftIndex)) > 0) {
leftIndex++;
// data[j] 是 leftChild 和 rightChild 中的最大值
}
// 比最大的还打,则结束
if (data.get(k).compareTo(data.get(leftIndex)) >= 0) {
break;
}
// 交换
data.swap(k, leftIndex);
k = leftIndex;
}
}
// 看堆中的最大元素
public E findMax() {
if (data.getSize() == 0) {
throw new IllegalArgumentException("Can not findMax when heap is empty.");
}
return data.get(0);
}
实现自己的优先队列
优先队列(priority queue)
普通的队列是一种先进先出的数据结构,元素在队列尾追加,而从队列头删除。在优先队列中,元素被赋予优先级。当访问元素时,具有最高优先级的元素最先删除。优先队列具有最高级先出 (first in, largest out)的行为特征。通常采用堆数据结构来实现。
为什么不排序后去执行,而是使用优先队列?
场景:游戏打怪物,打优先级高(最弱,最强)的敌人,而敌人是不断变化的。
场景:操作系统分配资源,动态选择。因为任务是不断变化的
public interface Queue<E> {
int getSize();
boolean isEmpty();
// 添加元素
void enqueue(E e);
// 删除元素
E dequeue();
// 拿到当前最大
E getFront();
}
public class PriorityQueue<E extends Comparable<E>> implements Queue<E> {
private MaxHeap<E> maxHeap;
public PriorityQueue(){
maxHeap = new MaxHeap<>();
}
@Override
public int getSize(){
return maxHeap.size();
}
@Override
public boolean isEmpty(){
return maxHeap.isEmpty();
}
@Override
public E getFront(){
return maxHeap.findMax();
}
@Override
public void enqueue(E e){
maxHeap.add(e);
}
@Override
public E dequeue(){
return maxHeap.extractMax();
}
}
四:并查集
并查集解决连接问题
并查集:一种树型的数据结构,用于处理一些不相交集合(Disjoint Sets)的合并及查询问题。

连接不是路径问题,比路径回答的问题少。
场景:

前提: 江湖上散落着各式各样的大侠,有上千个之多。整天背着剑在外面走来走去,特点:碰到和自己不是一路人的,就要打一架,他们很讲义气,绝对不打自己的朋友。而且他们信奉“朋友的朋友就是我的朋友”,只要是能通过朋友关系串联起来的,不管拐了多少个弯,都认为是自己人。
如何区分是不是一路人:每个朋友圈内推举出一个比较有名望的人,作为该圈子的代表人物,这样,每个圈子就可以这样命名“齐达内朋友之队”“罗纳尔多朋友之队”,两人只要互相对一下自己的队长是不是同一个人,就可以确定敌友关系了。
队内所有人实行分等级制度,形成树状结构,我队长就是根节点,下面分别是二级队员、三级队员。每人记住自己的上级是谁就行了。遇到判断敌友的时候,只要一层层向上问,直到最高层,就可以在短时间内确定队长是谁了。
连接不是路径 由于我们关心的只是两个人之间是否连通,至于他们是如何连通的,以及每个圈子内部的结构是怎样的,甚至队长是谁,并不重要。
并查集一
package com.wangpp.study.数据结构.树.并查集;
// 我们的第一版Union-Find
public class UnionFind1 implements UF {
private int[] id;
public UnionFind1(int size) {
id = new int[size];
// 初始化, 每一个id[i]指向自己, 没有合并的元素
for (int i = 0; i < size; i++) {
id[i] = i;
}
}
@Override
public int getSize() {
return id.length;
}
// 查找元素p所对应的集合编号
// O(1)复杂度
private int find(int p) {
if (p < 0 || p >= id.length) {
throw new IllegalArgumentException("p is out of bound.");
}
return id[p];
}
// 查看元素p和元素q是否所属一个集合
// O(1)复杂度
@Override
public boolean isConnected(int p, int q) {
return find(p) == find(q);
}
// 合并元素p和元素q所属的集合
// O(n) 复杂度
@Override
public void unionElements(int p, int q) {
int pID = find(p);
int qID = find(q);
if (pID == qID){
return;
}
/**
* 合并过程需要遍历一遍所有元素, 将两个元素的所属集合编号合并
*
* 0,1,2,3,4,5
* -----------
* 0,1,0,1,0,1
*
* unionElements(0,3)
* 全部链接
* 0,1,2,3,4,5
* -----------
* 1,1,1,1,1,1
*/
for (int i = 0; i < id.length; i++){
// pID=0
if (id[i] == pID){
// qID=1
id[i] = qID;
}
}
}
}
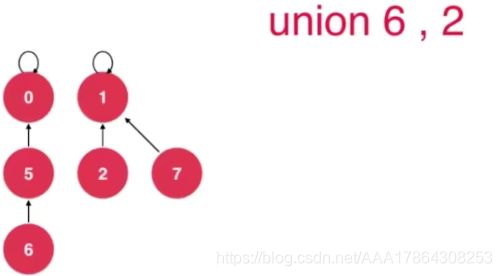
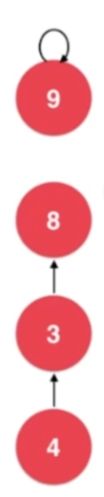
并查集二
package com.wangpp.study.数据结构.树.并查集;
// 我们的第二版Union-Find
public class UnionFind2 implements UF {
// 我们的第二版Union-Find, 使用一个数组构建一棵指向父节点的树
// parent[i]表示第一个元素所指向的父节点
private int[] parent;
// 构造函数
public UnionFind2(int size) {
parent = new int[size];
// 初始化, 每一个parent[i]指向自己, 表示每一个元素自己自成一个集合
for (int i = 0; i < size; i++) {
parent[i] = i;
}
}
@Override
public int getSize() {
return parent.length;
}
// 查找过程, 查找元素p所对应的集合编号
// O(h)复杂度, h为树的高度
private int find(int p) {
if (p < 0 || p >= parent.length) {
throw new IllegalArgumentException("p is out of bound.");
}
// 不断去查询自己的父亲节点, 直到到达根节点
// 根节点的特点: parent[p] == p
while (p != parent[p]) {
p = parent[p];
}
return p;
}
// 查看元素p和元素q是否所属一个集合
// O(h)复杂度, h为树的高度
@Override
public boolean isConnected(int p, int q) {
return find(p) == find(q);
}
// 合并元素p和元素q所属的集合
// O(h)复杂度, h为树的高度
@Override
public void unionElements(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if (pRoot == qRoot) {
return;
}
parent[pRoot] = qRoot;
}
}
并查集二小优化
@Override
public void unionElements(int p, int q){
int pRoot = find(p);
int qRoot = find(q);
if(pRoot == qRoot)
return;
// 根据两个元素所在树的元素个数不同判断合并方向
// 将元素个数少的集合合并到元素个数多的集合上
if(sz[pRoot] < sz[qRoot]){
parent[pRoot] = qRoot;
sz[qRoot] += sz[pRoot];
}
else{ // sz[qRoot] <= sz[pRoot]
parent[qRoot] = pRoot;
sz[pRoot] += sz[qRoot];
}
}
五:线段树(区间树)
线段树
线段树,类似区间树,是一个完全二叉树,它在各个节点保存一条线段(数组中的一段子数组),主要用于高效解决连续区间的动态查询问题,由于二叉结构的特性,它基本能保持每个操作的复杂度为O(lgN)!
线段树的适用范围很广,可以在线维护修改以及查询区间上的最值,求和。更可以扩充到二维线段树(矩阵树)和三维线段树(空间树)。对于一维线段树来说,每次更新以及查询的时间复杂度为O(logN)。

每个节点存储的是区间的信息
如区间最大值,当然也可以计算区间之和区间最小值等。

对于A[1:6] = {1,8,6,4,3,5}来说,线段树如上所示,红色代表每个结点存储的区间,蓝色代表该区间最值。
可以发现,每个叶子结点的值就是数组的值,每个非叶子结点的度都为二,且左右两个孩子分别存储父亲一半的区间。每个父亲的存储的值也就是两个孩子存储的值的最大值。
一般用数组存储

对于上述线段树,我们增加绿色数字为每个结点的下标
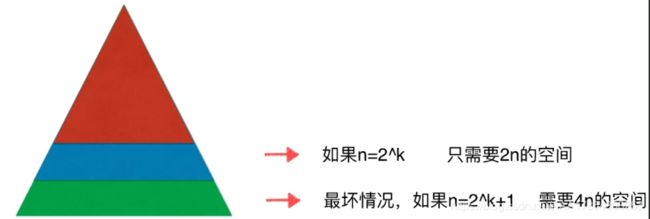
线段树需要的空间为数组大小的四倍
代码
public class SegmentTree<E> {
private E[] tree;
private E[] data;
private Merger<E> merger;
public SegmentTree(E[] arr, Merger<E> merger) {
this.merger = merger;
// 数据初始化
data = (E[]) new Object[arr.length];
for (int i = 0; i < arr.length; i++) {
data[i] = arr[i];
}
// 四倍空间
tree = (E[]) new Object[4 * arr.length];
buildSegmentTree(0, 0, arr.length - 1);
}
// 返回完全二叉树的数组表示中,一个索引所表示的元素的左孩子节点的索引
private int leftChild(int index) {
return 2 * index + 1;
}
// 返回完全二叉树的数组表示中,一个索引所表示的元素的右孩子节点的索引
private int rightChild(int index) {
return 2 * index + 2;
}
}
创建线段树

创建根必须要先创建好左右两个子树根节点,子树根节点以此类推。
直到不能再划分
// 在treeIndex的位置创建表示区间[l...r]的线段树[0.0.9]
private void buildSegmentTree(int treeIndex, int l, int r) {
// 递归结束条件
if (l == r) {
tree[treeIndex] = data[l];
return;
}
// leftTreeIndex = 1
int leftTreeIndex = leftChild(treeIndex);
// rightTreeIndex = 2
int rightTreeIndex = rightChild(treeIndex);
// int mid = 4;
int mid = l + (r - l) / 2;
// 创建左子树 1,1,4
buildSegmentTree(leftTreeIndex, l, mid);
// 创建右子树 2,5,9
buildSegmentTree(rightTreeIndex, mid + 1, r);
// 当前节点 merger.merge为业务函数
tree[treeIndex] = merger.merge(tree[leftTreeIndex], tree[rightTreeIndex]);
}
public interface Merger<E> {
E merge(E a, E b);
}
SegmentTree<Integer> segTree = new SegmentTree<>(nums,
(a, b) -> a + b);
区间查询
我们知道线段树的每个结点存储的都是一段区间的信息 ,如果我们刚好要查询这个区间,那么则直接返回这个结点的信息即可,比如对于上面线段树,如果我直接查询[1,6]这个区间的最值,那么直接返回根节点信息返回13即可,但是一般我们不会凑巧刚好查询那些区间,比如现在我要查询[2,5]区间的最值

一共有5个区间,而且我们可以发现[4,5]这个区间已经包含了两个子树的信息,所以我们需要查询的区间只有三个,分别是[2,2],[3,3],[4,5],到这里你能通过更新的思路想出来查询的思路吗? 我们还是从根节点开始往下递归,如果当前结点是要查询的区间的真子集,则返回这个结点的信息且不需要再往下递归了。
// 返回区间[queryL, queryR]的值
public E query(int queryL, int queryR) {
if (queryL < 0 || queryL >= data.length ||
queryR < 0 || queryR >= data.length || queryL > queryR) {
throw new IllegalArgumentException("Index is illegal.");
}
return query(0, 0, data.length - 1, queryL, queryR);
}
// 在以treeIndex为根的线段树中[l...r]的范围里,搜索区间[queryL...queryR]的值前三个表示节点信息
private E query(int treeIndex, int l, int r, int queryL, int queryR) {
// 查询区间恰好为treeIndex表示的区间范围
if (l == queryL && r == queryR) {
return tree[treeIndex];
}
// 查询两个孩子对应的索引
int leftTreeIndex = leftChild(treeIndex);
int rightTreeIndex = rightChild(treeIndex);
int mid = l + (r - l) / 2;
// 用户关心的区间与左孩子无关直接在右面查找
if (queryL >= mid + 1) {
return query(rightTreeIndex, mid + 1, r, queryL, queryR);
}
// 用户关心的区间与右孩子无关直接在左面查找
else if (queryR <= mid) {
return query(leftTreeIndex, l, mid, queryL, queryR);
}
// 在左节点找一下
E leftResult = query(leftTreeIndex, l, mid, queryL, mid);
// 在右节点找一下
E rightResult = query(rightTreeIndex, mid + 1, r, mid + 1, queryR);
return merger.merge(leftResult, rightResult);
}
六:平衡二叉树
AVL 树是一种平衡二叉树,得名于其发明者的名字( Adelson-Velskii 以及 Landis)。平衡二叉树递归定义如下:
左右子树的高度差小于等于 1。
其每一个子树均为平衡二叉树。
基于这一句话,我们就可以进行判断其一棵树是否为平衡二叉了。
目的:避免二分搜索树退化为链表
特征
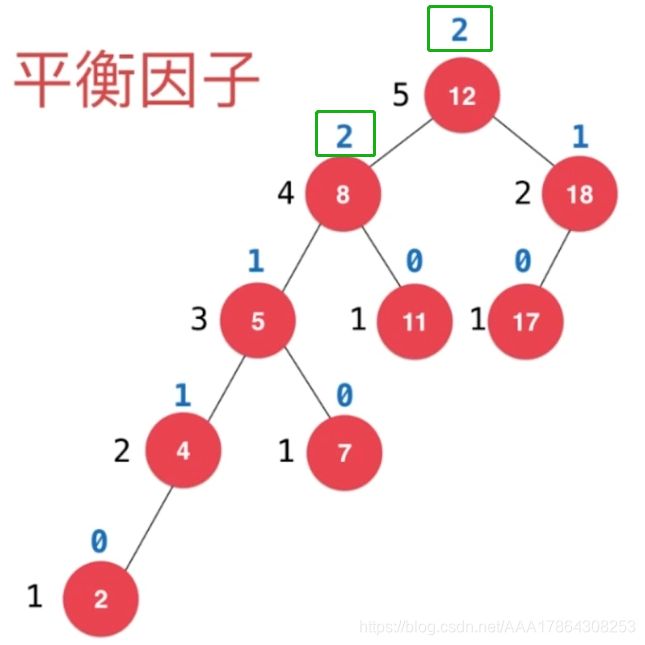
平衡因子
旋转
只有插入节点时才会不平衡(平衡因子大于一)
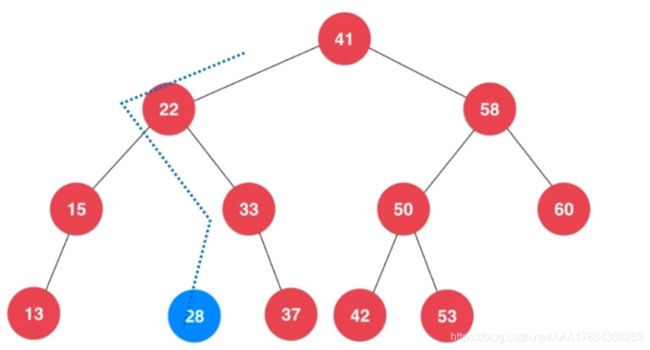
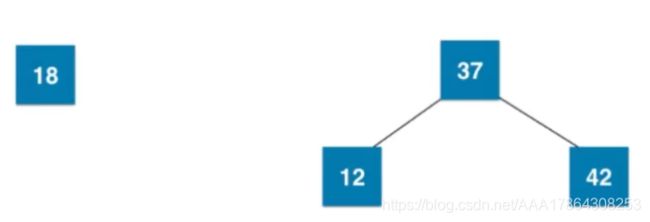
4种平衡调整如下(结点的数字仅作标记作用):
①LL:右单旋转

②RR:左单旋转
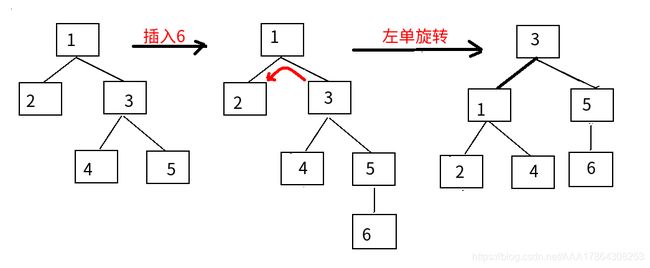
③LR平衡旋转:先左后右
平衡二叉树查找:平衡二叉树查找过程等同于二叉排序树相同,因此平衡二叉树查找长度不超过数的长度,及其平均查找长度为O(log2n)。
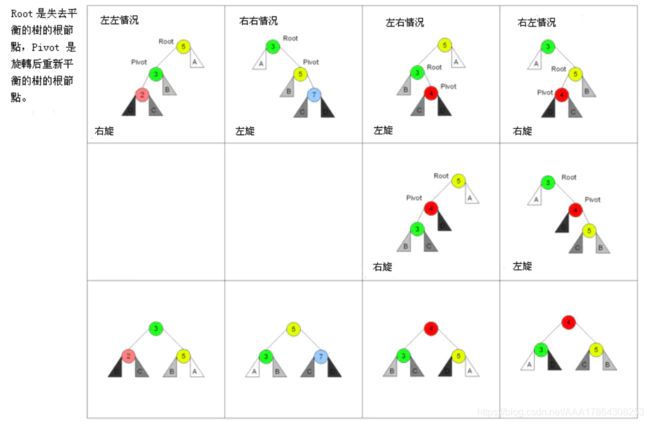
辅助函数
判断是否平衡二叉树:递归判断左右子书高度差
判断是否二分搜索树:中序是否有序
package com.wangpp.study.数据结构.树.平衡二叉树;
import java.util.ArrayList;
public class AVLTree<K extends Comparable<K>, V> {
private class Node {
public K key;
public V value;
public Node left, right;
public int height;
public Node(K key, V value) {
this.key = key;
this.value = value;
left = null;
right = null;
height = 1;
}
}
private Node root;
private int size;
public AVLTree() {
root = null;
size = 0;
}
public int getSize() {
return size;
}
public boolean isEmpty() {
return size == 0;
}
// 判断该二叉树是否是一棵二分搜索树
public boolean isBST() {
ArrayList<K> keys = new ArrayList<>();
inOrder(root, keys);
for (int i = 1; i < keys.size(); i++)
if (keys.get(i - 1).compareTo(keys.get(i)) > 0)
return false;
return true;
}
private void inOrder(Node node, ArrayList<K> keys) {
if (node == null) {
return;
}
inOrder(node.left, keys);
keys.add(node.key);
inOrder(node.right, keys);
}
// 判断该二叉树是否是一棵平衡二叉树
public boolean isBalanced() {
return isBalanced(root);
}
// 判断以Node为根的二叉树是否是一棵平衡二叉树,递归算法
private boolean isBalanced(Node node) {
if (node == null) {
return true;
}
int balanceFactor = getBalanceFactor(node);
if (Math.abs(balanceFactor) > 1) {
return false;
}
return isBalanced(node.left) && isBalanced(node.right);
}
// 获得节点node的高度
private int getHeight(Node node) {
if (node == null) {
return 0;
}
return node.height;
}
// 获得节点node的平衡因子
private int getBalanceFactor(Node node) {
if (node == null) {
return 0;
}
return getHeight(node.left) - getHeight(node.right);
}
// 对节点y进行向右旋转操作,返回旋转后新的根节点x
// y x
// / \ / \
// x T4 向右旋转 (y) z y
// / \ - - - - - - - -> / \ / \
// z T3 T1 T2 T3 T4
// / \
// T1 T2
private Node rightRotate(Node y) {
Node x = y.left;
Node T3 = x.right;
// 向右旋转过程
x.right = y;
y.left = T3;
// 更新height
y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;
return x;
}
// 对节点y进行向左旋转操作,返回旋转后新的根节点x
// y x
// / \ / \
// T1 x 向左旋转 (y) y z
// / \ - - - - - - - -> / \ / \
// T2 z T1 T2 T3 T4
// / \
// T3 T4
private Node leftRotate(Node y) {
Node x = y.right;
Node T2 = x.left;
// 向左旋转过程
x.left = y;
y.right = T2;
// 更新height
y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;
return x;
}
// 向二分搜索树中添加新的元素(key, value)
public void add(K key, V value) {
root = add(root, key, value);
}
// 向以node为根的二分搜索树中插入元素(key, value),递归算法
// 返回插入新节点后二分搜索树的根
private Node add(Node node, K key, V value) {
if (node == null) {
size++;
return new Node(key, value);
}
if (key.compareTo(node.key) < 0)
node.left = add(node.left, key, value);
else if (key.compareTo(node.key) > 0)
node.right = add(node.right, key, value);
else // key.compareTo(node.key) == 0
node.value = value;
// 更新height
node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));
// 计算平衡因子
int balanceFactor = getBalanceFactor(node);
// 平衡维护
if (balanceFactor > 1 && getBalanceFactor(node.left) >= 0)
return rightRotate(node);
if (balanceFactor < -1 && getBalanceFactor(node.right) <= 0)
return leftRotate(node);
if (balanceFactor > 1 && getBalanceFactor(node.left) < 0) {
node.left = leftRotate(node.left);
return rightRotate(node);
}
if (balanceFactor < -1 && getBalanceFactor(node.right) > 0) {
node.right = rightRotate(node.right);
return leftRotate(node);
}
return node;
}
// 返回以node为根节点的二分搜索树中,key所在的节点
private Node getNode(Node node, K key) {
if (node == null) {
return null;
}
if (key.equals(node.key)) {
return node;
} else if (key.compareTo(node.key) < 0) {
return getNode(node.left, key);
} else {
return getNode(node.right, key);
}
}
public boolean contains(K key) {
return getNode(root, key) != null;
}
public V get(K key) {
Node node = getNode(root, key);
return node == null ? null : node.value;
}
public void set(K key, V newValue) {
Node node = getNode(root, key);
if (node == null) {
throw new IllegalArgumentException(key + " doesn't exist!");
}
node.value = newValue;
}
// 返回以node为根的二分搜索树的最小值所在的节点
private Node minimum(Node node) {
if (node.left == null)
return node;
return minimum(node.left);
}
// 删除掉以node为根的二分搜索树中的最小节点
// 返回删除节点后新的二分搜索树的根
private Node removeMin(Node node) {
if (node.left == null) {
Node rightNode = node.right;
node.right = null;
size--;
return rightNode;
}
node.left = removeMin(node.left);
return node;
}
// 从二分搜索树中删除键为key的节点
public V remove(K key) {
Node node = getNode(root, key);
if (node != null) {
root = remove(root, key);
return node.value;
}
return null;
}
private Node remove(Node node, K key) {
if (node == null)
return null;
if (key.compareTo(node.key) < 0) {
node.left = remove(node.left, key);
return node;
} else if (key.compareTo(node.key) > 0) {
node.right = remove(node.right, key);
return node;
} else { // key.compareTo(node.key) == 0
// 待删除节点左子树为空的情况
if (node.left == null) {
Node rightNode = node.right;
node.right = null;
size--;
return rightNode;
}
// 待删除节点右子树为空的情况
if (node.right == null) {
Node leftNode = node.left;
node.left = null;
size--;
return leftNode;
}
// 待删除节点左右子树均不为空的情况
// 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
// 用这个节点顶替待删除节点的位置
Node successor = minimum(node.right);
successor.right = removeMin(node.right);
successor.left = node.left;
node.left = node.right = null;
return successor;
}
}
public static void main(String[] args) {
System.out.println("Pride and Prejudice");
ArrayList<String> words = new ArrayList<>();
if (FileOperation.readFile("pride-and-prejudice.txt", words)) {
System.out.println("Total words: " + words.size());
AVLTree<String, Integer> map = new AVLTree<>();
for (String word : words) {
if (map.contains(word))
map.set(word, map.get(word) + 1);
else
map.add(word, 1);
}
System.out.println("Total different words: " + map.getSize());
System.out.println("Frequency of PRIDE: " + map.get("pride"));
System.out.println("Frequency of PREJUDICE: " + map.get("prejudice"));
System.out.println("is BST : " + map.isBST());
System.out.println("is Balanced : " + map.isBalanced());
}
System.out.println();
}
}
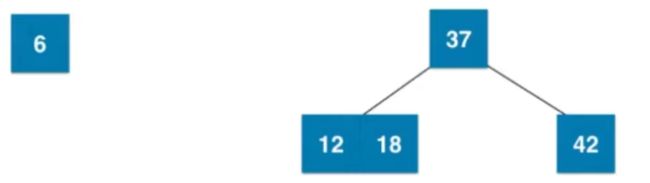
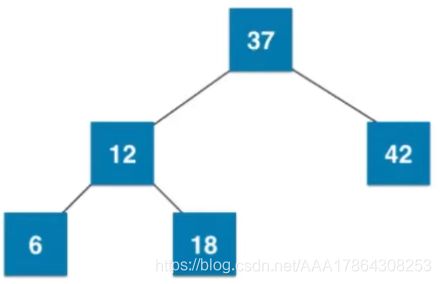
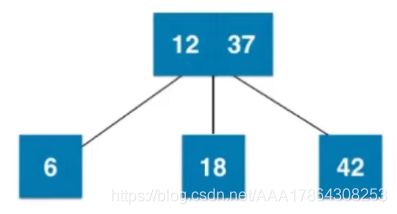
七:二三树
B树(平衡多路查找树)
2-3,2-3-4等都属于B树
一个m阶的B树具有如下几个特征:
1.根结点至少有两个子女。
2.每个中间节点都至少包含ceil(m / 2)个孩子,最多有m个孩子。
3.每一个叶子节点都包含k-1个元素,其中 m/2 <= k <= m。
4.所有的叶子结点都位于同一层。
5.每个节点中的元素从小到大排列
实例:
M = 4 阶,(2, 4)树。 最多含有 3个关键字 和 4个子树
M = 5 阶,(3, 5)树。 最多含有 4个关键字 和 5个子树
M = 6 阶,(3, 6)树。 最多含有 5个关键字 和 6个子树
二三树基本概念

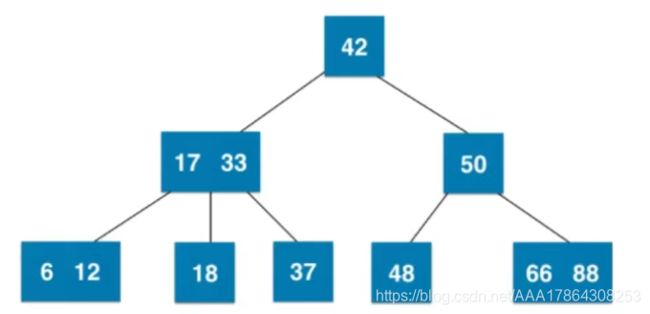
特点:绝对平衡的树(根到叶子节点经过的节点数量都是相同的)
添加节点永远不会添加到新的位置维持据对平衡
添加节点的过程
八:红黑树
二三树转为红黑树
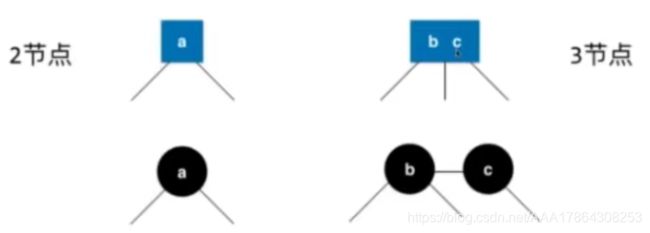
为了表示关系,将线段标红,表示并列关系

可以做特殊标识
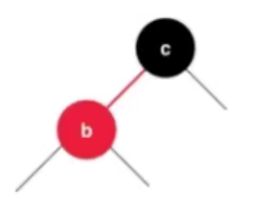
所有红色向左倾斜

红黑树定义

说明:红黑树中NULL结点为黑
-第二条(做对比)
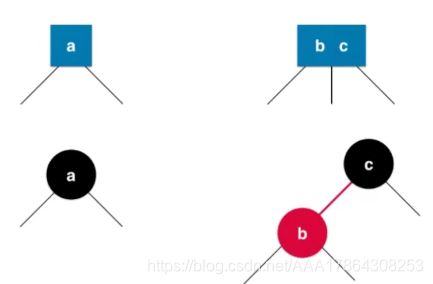
-第五条(满二叉树层次)
新增节点
添加新元素
- 最复杂添加的比红色大 -1
- 添加的比红色小 -2
- 添加的比黑色大 -3
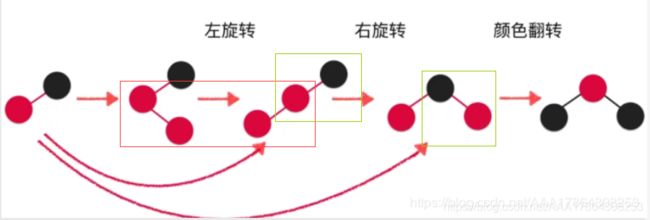
code
package teacher
import java.util.ArrayList;
public class RBTree<K extends Comparable<K>, V> {
private static final boolean RED = true;
private static final boolean BLACK = false;
private class Node{
public K key;
public V value;
public Node left, right;
public boolean color;
public Node(K key, V value){
this.key = key;
this.value = value;
left = null;
right = null;
color = RED;
}
}
private Node root;
private int size;
public RBTree(){
root = null;
size = 0;
}
public int getSize(){
return size;
}
public boolean isEmpty(){
return size == 0;
}
// 判断节点node的颜色
private boolean isRed(Node node){
if(node == null)
return BLACK;
return node.color;
}
// node x
// / \ 左旋转 / \
// T1 x ---------> node T3
// / \ / \
// T2 T3 T1 T2
private Node leftRotate(Node node){
Node x = node.right;
// 左旋转
node.right = x.left;
x.left = node;
x.color = node.color;
node.color = RED;
return x;
}
// node x
// / \ 右旋转 / \
// x T2 -------> y node
// / \ / \
// y T1 T1 T2
private Node rightRotate(Node node){
Node x = node.left;
// 右旋转
node.left = x.right;
x.right = node;
x.color = node.color;
node.color = RED;
return x;
}
// 颜色翻转
private void flipColors(Node node){
node.color = RED;
node.left.color = BLACK;
node.right.color = BLACK;
}
// 向红黑树中添加新的元素(key, value)
public void add(K key, V value){
root = add(root, key, value);
root.color = BLACK; // 最终根节点为黑色节点
}
// 向以node为根的红黑树中插入元素(key, value),递归算法
// 返回插入新节点后红黑树的根
private Node add(Node node, K key, V value){
if(node == null){
size ++;
return new Node(key, value); // 默认插入红色节点
}
if(key.compareTo(node.key) < 0)
node.left = add(node.left, key, value);
else if(key.compareTo(node.key) > 0)
node.right = add(node.right, key, value);
else // key.compareTo(node.key) == 0
node.value = value;
if (isRed(node.right) && !isRed(node.left))
node = leftRotate(node);
if (isRed(node.left) && isRed(node.left.left))
node = rightRotate(node);
if (isRed(node.left) && isRed(node.right))
flipColors(node);
return node;
}
// 返回以node为根节点的二分搜索树中,key所在的节点
private Node getNode(Node node, K key){
if(node == null)
return null;
if(key.equals(node.key))
return node;
else if(key.compareTo(node.key) < 0)
return getNode(node.left, key);
else // if(key.compareTo(node.key) > 0)
return getNode(node.right, key);
}
public boolean contains(K key){
return getNode(root, key) != null;
}
public V get(K key){
Node node = getNode(root, key);
return node == null ? null : node.value;
}
public void set(K key, V newValue){
Node node = getNode(root, key);
if(node == null)
throw new IllegalArgumentException(key + " doesn't exist!");
node.value = newValue;
}
// 返回以node为根的二分搜索树的最小值所在的节点
private Node minimum(Node node){
if(node.left == null)
return node;
return minimum(node.left);
}
// 删除掉以node为根的二分搜索树中的最小节点
// 返回删除节点后新的二分搜索树的根
private Node removeMin(Node node){
if(node.left == null){
Node rightNode = node.right;
node.right = null;
size --;
return rightNode;
}
node.left = removeMin(node.left);
return node;
}
// 从二分搜索树中删除键为key的节点
public V remove(K key){
Node node = getNode(root, key);
if(node != null){
root = remove(root, key);
return node.value;
}
return null;
}
private Node remove(Node node, K key){
if( node == null )
return null;
if( key.compareTo(node.key) < 0 ){
node.left = remove(node.left , key);
return node;
}
else if(key.compareTo(node.key) > 0 ){
node.right = remove(node.right, key);
return node;
}
else{ // key.compareTo(node.key) == 0
// 待删除节点左子树为空的情况
if(node.left == null){
Node rightNode = node.right;
node.right = null;
size --;
return rightNode;
}
// 待删除节点右子树为空的情况
if(node.right == null){
Node leftNode = node.left;
node.left = null;
size --;
return leftNode;
}
// 待删除节点左右子树均不为空的情况
// 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
// 用这个节点顶替待删除节点的位置
Node successor = minimum(node.right);
successor.right = removeMin(node.right);
successor.left = node.left;
node.left = node.right = null;
return successor;
}
}
public static void main(String[] args){
}
}
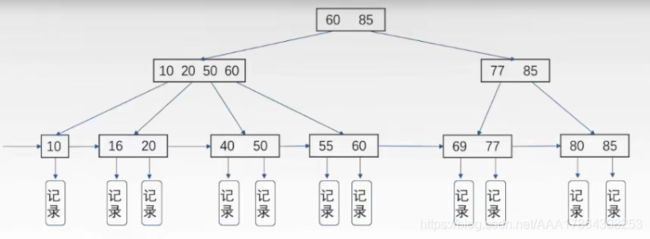
九:B+树
一个m阶的B+树具有如下几个特征:
非叶子节点:记录叶子节点最大值的索引,无记录
叶子节点:有记录
中间一条指针链表穿着整个叶子节点,便于顺序查找。
B+树的优势:
1.单一节点存储更多的元素,使得查询的IO次数更少。
2.所有查询都要查找到叶子节点,查询性能稳定。
3.所有叶子节点形成有序链表,便于范围查询。
公众号内回复“树”即可获取完整的代码
更多前沿技术,面试技巧,内推信息请扫码关注公众号“云计算平台技术”
![]()