Python非线性回归预测模型实验完整版
非线性回归预测模型
实验目的
通过非线性回归预测模型,掌握预测模型的建立和应用方法,了解非线性回归模型的基本原理
实验内容
非线性回归预测模型
实验步骤和过程
(1)第一步:学习非线性回归预测模型相关知识。
非线性回归预测模型是指建立预测变量与自变量之间的非线性关系的模型,通常用来预测因变量的值。在非线性回归模型中,因变量与自变量的关系可以是曲线、指数、对数等非线性形式,而不是线性形式。
根据自变量的个数,非线性回归模型可以分为一元非线性回归模型和多元非线性回归模型。一元非线性回归模型中只有一个自变量,多元非线性回归模型中有两个或多个自变量。根据模型的形式,非线性回归模型可以分为参数模型和非参数模型。参数模型是指模型的形式已知,但是模型中的参数需要通过训练数据来确定,如多项式回归模型和指数回归模型等。非参数模型是指模型的形式未知,需要通过训练数据来确定,如神经网络模型和支持向量机模型等。
与线性回归模型相比,非线性回归模型具有以下特点:
1.非线性关系:非线性回归模型可以描述因变量与自变量之间的非线性关系,适用于实际问题中非线性关系较为明显的情况。
2.复杂度高:由于非线性回归模型的形式多样,建模过程比较复杂,需要根据实际问题选择合适的模型。
3.参数估计困难:非线性回归模型中的参数通常需要通过迭代优化算法来估计,计算量较大,而且容易陷入局部最优解。
4.预测精度高:非线性回归模型可以更准确地预测因变量的值,适用于实际问题中需要高精度预测的情况。
5.建模方法 :非线性回归模型的建模方法包括参数估计和模型选择两个方面。参数估计是指在已知模型形式的情况下,通过训练数据来确定模型中的参数。模型选择是指在未知模型形式的情况下,根据训练数据来选择最优的模型形式。
6.参数估计:参数估计通常使用最小二乘法来求解。最小二乘法是一种常见的参数估计方法,其基本思想是使模型预测值与真实值之间的误差平方和最小。在非线性回归模型中,最小二乘法需要通过迭代优化算法来求解。常见的迭代优化算法包括梯度下降法和牛顿法等。
7.模型选择 模型选择通常使用交叉验证方法来确定最优的模型形式。交叉验证是一种常见的模型选择方法,其基本思想是将训练数据划分为若干个子集,每次用其中一个子集作为测试数据,其余子集作为训练数据来评估模型的性能。通过对不同模型形式进行交叉验证来选择最优的模型形式。
8.应用场景:非线性回归模型可以应用于许多领域,如金融、医疗、工业等。以下是一些典型的应用场景:
股票价格预测:股票价格受到众多因素的影响,非线性回归模型可以更准确地预测股票价格的走势。
医疗预测:非线性回归模型可以应用于医疗领域,如预测病人的生存时间、预测疾病的发生率等。
工业预测:非线性回归模型可以应用于工业领域,如预测销售额、预测产量等。
土壤污染预测:非线性回归模型可以应用于环境保护领域,如预测土壤中污染物的含量等。
总之,非线性回归模型是一种重要的预测模型,可以应用于许多领域。在实际应用中,需要根据实际问题选择合适的模型形式和参数估计方法来建立预测模型。
非线性模型公式推导过程
非线性模型是指因变量和自变量之间的关系不是简单的线性关系而是复杂的非线性关系的模型。非线性模型可以通过拟合数据来确定模型参数,从而预测未来的结果。下面是非线性模型公式推导的详细过程:
假设我们有n个样本,每个样本有m个自变量和一个因变量。我们用向量x表示自变量,向量y表示因变量,用函数f(x,θ)表示非线性模型,其中θ表示模型参数。
则非线性模型可以表示为: y = f(x, θ)
为了确定模型参数,我们需要最小化残差平方和,即:
min θ Σ(y - f(x, θ))^2
其中Σ表示求和符号。上述式子可以通过梯度下降法或牛顿法等方法求解。
对上式求导得: ∂(Σ(y - f(x, θ))^2) / ∂θ = -2Σ(y - f(x, θ)) * (∂f(x, θ) / ∂θ)
因此,我们需要求出函数f(x,θ)对θ的偏导数,
即: ∂f(x,θ) / ∂θ
这个偏导数可以通过求解函数f(x,θ)的导数来得到。具体而言,我们可以采用链式法则求导数,将f(x,θ)分解为多个函数的复合。
例如,如果我们有一个三次多项式模型:
f(x,θ) = θ0 + θ1x + θ2x^2 + θ3x^3
则对θ0的偏导数为: ∂f(x,θ) / ∂θ0 = 1
对θ1的偏导数为: ∂f(x,θ) / ∂θ1 = x
对θ2的偏导数为: ∂f(x,θ) / ∂θ2 = x^2
对θ3的偏导数为: ∂f(x,θ) / ∂θ3 = x^3
因此,我们可以将上述偏导数带入到上面的公式中,用梯度下降法或牛顿法等方法求解模型参数。
窗体顶端
窗体底端
(2)第二步:数据准备,数据来源于课本例题。
年份 客运量 X1/万人 旅客周转量 X2/亿人千米 公路客运量 X3/万人 公路旅客周转量 X4/亿人千米
1987 10091 88.4 8552 59.9
1988 10551 93.46 8864 64.81
1989 10389 94.01 8928 97.66
1990 10702 87.67 9475 65.77
1991 11078 95.86 9880 71.83
1992 10565 99.98 9277 69.89
1993 11063 111.9 9528 73.38
1994 25163 146.87 23518 101.77
1995 21697 137.93 20095 93.1
1996 23904 149.94 22397.1 102.4
1997 25003.7 172.4 23437.9 119.5
1998 29863 189.85 28048 131.8
1999 32962.2 237.99 30796 164.2
2000 33704 237.94 31586 171.2
2001 39984.4 304.2 37909 232.76
2002 38879.6 281.6 36726 210.1
2003 35156 263.45 33039 192.87
2004 38902 317.76 36502 227.21
2005 41079 331.6 38509 233.12
2006 43844 362.4 40861 247.71
(3)第三步:使用 Python 编写实验代码并做图。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
# 读取Excel数据
data = pd.read_excel('E:\\File\\class\\大三下\\数据挖掘\\test3.xlsx')
# 将x和y值转换为numpy数组
x = np.array(data['年份'])
y = np.array(data['客运量 X1/万人'])
# 使用多项式拟合数据
p = np.polyfit(x, y, 2) # 二次项拟合
# 生成预测数据
x_new = np.array([2007]) # 预测的年份
y_new = p[0] * x_new**2 + p[1] * x_new + p[2]
print('2007年对应的客运量为:', y_new[0])
# 生成预测曲线数据
x_plot = np.linspace(1990, 2010, 100)
y_plot = p[0] * x_plot**2 + p[1] * x_plot + p[2]
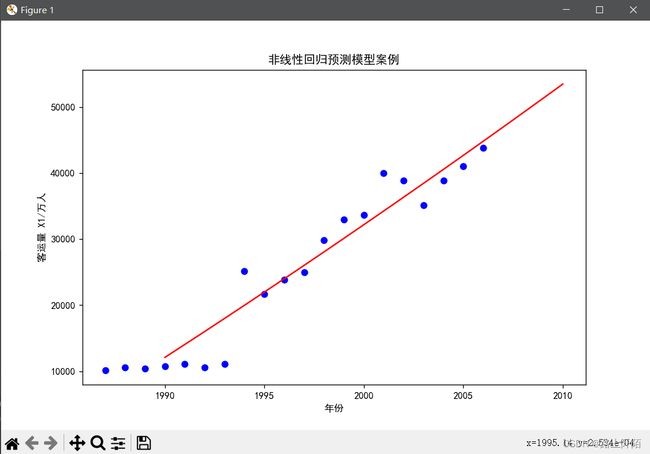
# 绘制图形
plt.scatter(x, y, color='blue')
plt.plot(x_plot, y_plot, color='red')
plt.title('非线性回归预测模型案例')
plt.xlabel('年份')
plt.ylabel('客运量 X1/万人')
plt.show()
代码解释:
上述代码是一个非线性回归预测模型案例,下面详细解释每个函数的功能、参数以及代码实现的过程。
1.导入库
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
pandas库:用于读取Excel数据。
numpy库:用于处理数组和数学计算。
matplotlib库:用于绘制图形。
2.设置中文字体
plt.rcParams[‘font.sans-serif’] = [‘SimHei’]
设置中文字体为SimHei,以便在图形中显示中文。
3.读取Excel数据
data = pd.read_excel(‘E:\File\class\大三下\数据挖掘\test3.xlsx’)
使用pandas库中的read_excel()函数读取Excel数据,将其存储在DataFrame对象data中。
4.将x和y值转换为numpy数组
x = np.array(data[‘年份’])
y = np.array(data[‘客运量 X1/万人’])
将DataFrame对象data中的’年份’和’客运量 X1/万人’列分别转换为numpy数组x和y。
5.使用多项式拟合数据
p = np.polyfit(x, y, 2)
使用numpy库中的polyfit()函数拟合数据,生成多项式系数p。这里使用二次项拟合。
6.生成预测数据
x_new = np.array([2007])
y_new = p[0] * x_new**2 + p[1] * x_new + p[2]
生成预测的年份x_new,然后使用多项式系数p计算对应的客运量y_new。
7.生成预测曲线数据
x_plot = np.linspace(1990, 2010, 100)
y_plot = p[0] * x_plot**2 + p[1] * x_plot + p[2]
生成100个等间隔的年份数据x_plot,然后使用多项式系数p计算对应的客运量y_plot,用于绘制预测曲线。
8.绘制图形
plt.scatter(x, y, color=‘blue’)
plt.plot(x_plot, y_plot, color=‘red’)
plt.title(‘非线性回归预测模型案例’)
plt.xlabel(‘年份’)
plt.ylabel(‘客运量 X1/万人’)
plt.show()
使用matplotlib库绘制散点图和预测曲线,设置图形标题、坐标轴标签,并显示图形。
总结:本案例使用了二次项多项式拟合数据,实现了非线性回归预测模型,并用图形展示了预测结果。代码的主要实现过程包括导入库、读取数据、拟合数据、生成预测数据、生成预测曲线数据、绘制图形等步骤。该代码的核心在于使用多项式拟合数据,这是非线性回归模型的基本思想之一。该代码还展示了如何使用matplotlib库绘制图形,并对图形进行美化。
(4)第四步:实验结果。
绘图和预测2007年的客运量X1。
这里的预测结果为:47003.86394734308
实验总结
通过本次实验,我学习了非线性回归预测模型的基本原理和建立方法,了解了如何使用Python编程实现预测模型。同时,我们也使用了某省会全社会客运量预测实例,对非线性回归模型进行了实际应用和分析。在实验中,我掌握了数据预处理、模型训练和结果评估等关键技术,对于今后的数据分析和预测工作将有很大的帮助。同时在这个过程之中也出现了一些问题,但通过查阅相关资料最终这些问题都得以解决。在这个过程中我的动手实践能力的到提升,也让我明白了实际动手操作的重要性,在实际操作中可以发现很多平时发现不了的问题,通过实践最终都得以解决。