CV中的注意力机制

注意力机制

计算机视觉中的注意力机制的基本思想 就是想让系统学会注意力 ，能够忽略无关信息，关注重点信息。

1. 硬注意力机制（Hard/Local Attention）

对每个输入项分配的权重非0即1，和软注意不同，硬注意机制只考虑那部分需要关注，哪部分不关注，也就是直接舍弃掉一些不相关项。优势在于可以减少一定的时间和计算成本，但有可能丢失掉一些本应该注意的信息。
硬注意力机制是一个不可微的注意力。
中心裁剪，最大池化层

2.软注意力机制

[0,1]间连续分布问题，每个区域被关注的程度高低，用0~1的score表示.软注意力的关键点在于，这种注意力更关注区域或者通道，而且软注意力是确定性的注意力，学习完成后直接可以通过网络生成，最关键的地方是软注意力是可微的，这是一个非常重要的地方。可以微分的注意力就可以通过神经网络算出梯度并且前向传播和后向反馈来学习得到注意力的权重。这种类型的软注意力在计算上是非常浪费的。

2.1Spatial Transformer Networks(空间域注意力)

class SpatialAttention(nn.Module):
    def __init__(self, kernel_size=7):
        super(SpatialAttention, self).__init__()
        assert kernel_size in (3,7), "kernel size must be 3 or 7"
        padding = 3if kernel_size == 7else1

        self.conv = nn.Conv2d(2,1,kernel_size, padding=padding, bias=False)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        avgout = torch.mean(x, dim=1, keepdim=True)
        maxout, _ = torch.max(x, dim=1, keepdim=True)
        x = torch.cat([avgout, maxout], dim=1)
        x = self.conv(x)
        return self.sigmoid(x)

2.2(Channel Attention Module)通道注意力

class ChannelAttention(nn.Module):
    def __init__(self, in_planes, rotio=16):
        super(ChannelAttention, self).__init__()
        self.avg_pool = nn.AdaptiveAvgPool2d(1)
        self.max_pool = nn.AdaptiveMaxPool2d(1)

        self.sharedMLP = nn.Sequential(
            nn.Conv2d(in_planes, in_planes // ratio, 1, bias=False), nn.ReLU(),
            nn.Conv2d(in_planes // rotio, in_planes, 1, bias=False))
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        avgout = self.sharedMLP(self.avg_pool(x))
        maxout = self.sharedMLP(self.max_pool(x))
        return self.sigmoid(avgout + maxout)

2.3（Branch Attention Module）分支注意力 - sknet

第一步使用的是分组卷积，原始feature map X 经过kernel size分别为，, , …以此类推的卷积核进行卷积后得到U1,U2,U3三个特征图，然后相加得到了U，U中融合了多个感受野的信息。然后得到的U是形状是[C,H,W]（C代表channel,H代表height, W代表width）的特征图，然后沿着H和W维度求平均值，最终得到了关于channel的信息是一个C×1×1的一维向量，代表的是各个通道的信息的重要程度。

之后再用一个线性变换，将原来的C维映射成Z维的信息，然后分别使用了三个线性变换，从Z维变为原来的C，这样完成了针对channel维度的信息提取，然后使用Softmax进行归一化，这时候每个channel对应一个分数，代表其channel的重要程度，这相当于一个mask。将这三个分别得到的mask分别乘以对应的U1,U2,U3，得到A1,A2,A3。然后三个模块相加，进行信息融合，得到最终模块A， 模块A相比于最初的X经过了信息的提炼，融合了多个感受野的信息。

import torch.nn as nn
import torch

class SKConv(nn.Module):
    def __init__(self, features, WH, M, G, r, stride=1, L=32):
        super(SKConv, self).__init__()
        d = max(int(features / r), L)
        self.M = M
        self.features = features
        self.convs = nn.ModuleList([])
        for i in range(M):
            # 使用不同kernel size的卷积
            self.convs.append(
                nn.Sequential(
                    nn.Conv2d(features,
                              features,
                              kernel_size=3 + i * 2,
                              stride=stride,
                              padding=1 + i,
                              groups=G), nn.BatchNorm2d(features),
                    nn.ReLU(inplace=False)))
            
        self.fc = nn.Linear(features, d)
        self.fcs = nn.ModuleList([])
        for i in range(M):
            self.fcs.append(nn.Linear(d, features))
        self.softmax = nn.Softmax(dim=1)

    def forward(self, x):
        for i, conv in enumerate(self.convs):
            fea = conv(x).unsqueeze_(dim=1)
            if i == 0:
                feas = fea
            else:
                feas = torch.cat([feas, fea], dim=1)
        fea_U = torch.sum(feas, dim=1)
        fea_s = fea_U.mean(-1).mean(-1)
        fea_z = self.fc(fea_s)
        for i, fc in enumerate(self.fcs):
            print(i, fea_z.shape)
            vector = fc(fea_z).unsqueeze_(dim=1)
            print(i, vector.shape)
            if i == 0:
                attention_vectors = vector
            else:
                attention_vectors = torch.cat([attention_vectors, vector],
                                              dim=1)
        attention_vectors = self.softmax(attention_vectors)
        attention_vectors = attention_vectors.unsqueeze(-1).unsqueeze(-1)
        fea_v = (feas * attention_vectors).sum(dim=1)
        return fea_v

if __name__ == "__main__":
    t = torch.ones((32, 256, 24,24))
    sk = SKConv(256,WH=1,M=2,G=1,r=2)
    out = sk(t)
    print(out.shape)

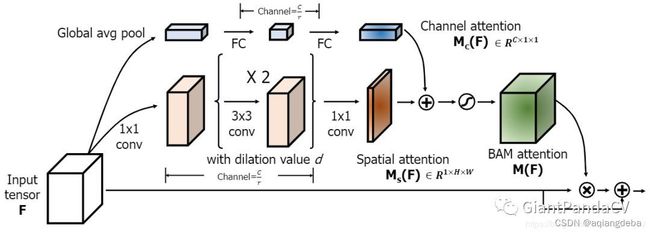
2.4Convolutional Block Attention Module(通道域+空间域)

class BasicBlock(nn.Module):
    expansion = 1
    def __init__(self, inplanes, planes, stride=1, downsample=None):
        super(BasicBlock, self).__init__()
        self.conv1 = conv3x3(inplanes, planes, stride)
        self.bn1 = nn.BatchNorm2d(planes)
        self.relu = nn.ReLU(inplace=True)
        self.conv2 = conv3x3(planes, planes)
        self.bn2 = nn.BatchNorm2d(planes)
        self.ca = ChannelAttention(planes)
        self.sa = SpatialAttention()
        self.downsample = downsample
        self.stride = stride
    def forward(self, x):
        residual = x
        out = self.conv1(x)
        out = self.bn1(out)
        out = self.relu(out)
        out = self.conv2(out)
        out = self.bn2(out)
        out = self.ca(out) * out  # 广播机制
        out = self.sa(out) * out  # 广播机制
        if self.downsample isnotNone:
            residual = self.downsample(x)
        out += residual
        out = self.relu(out)
        return out

2.5 Non-Local Attention

针对远距离信息传递问题，提高长距离依赖，本论文从传统的非局部均值滤波方法中受到启发，提出了卷积网络中的non-local，即：某一像素点处的响应是其他所有点处的特征权重和，将每一个点与其他所有点相关联，实现non-local 思想。

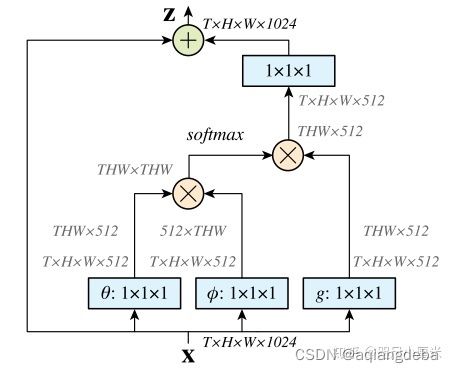
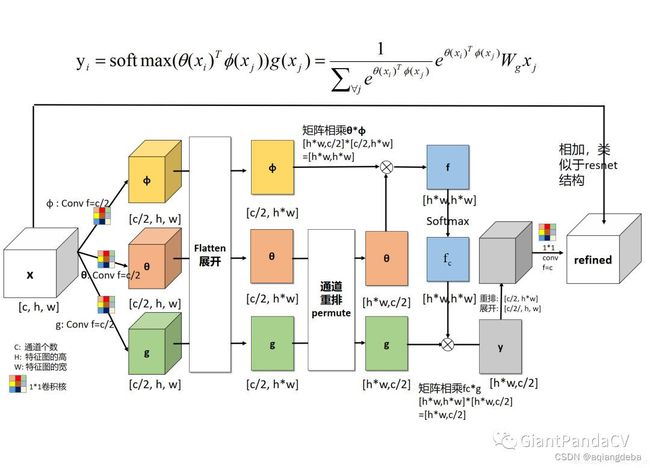
X是一个feature map,形状为[bs, c, h, w], 经过三个1×1卷积核，将通道缩减为原来一半（c/2）。然后将h,w两个维度进行flatten，变为h×w，最终形状为[bs, c/2, h×w]的tensor。对θ对应的tensor进行通道重排，在线性代数中也就是转置，得到形状为[bs, h×w, c/2]。然后与φ代表的tensor进行矩阵乘法，得到一个形状为[bs, h×w，h×w]的矩阵，这个矩阵计算的是相似度（或者理解为attention）。然后经过softmax进行归一化，然后将该得到的矩阵 fc 与g 经过flatten和转置的结果进行矩阵相乘，得到的形状为[bs, h*w, c/2]的结果y。然后转置为[bs, c/2, h×w]的tensor, 然后将h×w维度重新伸展为[h, w]，从而得到了形状为[bs, c/2, h, w]的tensor。然后对这个tensor再使用一个1×1卷积核，将通道扩展为原来的c，这样得到了[bs, c, h, w]的tensor,与初始X的形状是一致的。最终一步操作是将X与得到的tensor进行相加(类似resnet中的residual block)。