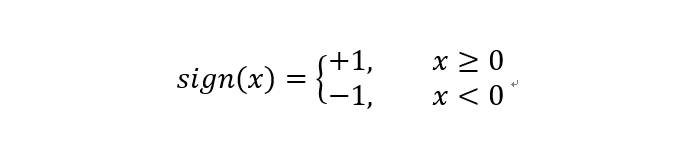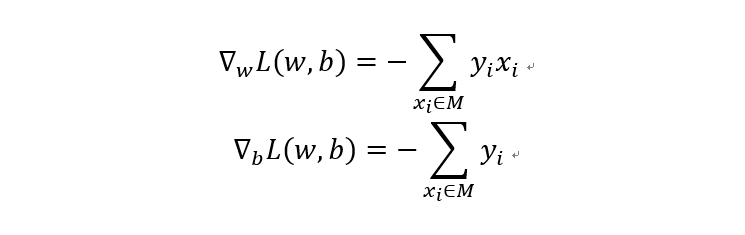机器学习之感知机原理及Python实现
机器学习算法感知机(perceptron)。感知机是一种较为简单的二分类模型,但由简至繁,感知机却是神经网络和支持向量机的基础。感知机旨在学习能够将输入数据划分为+1/-1的线性分离超平面,所以说整体而言感知机是一种线性模型。因为是线性模型,所以感知机的原理并不复杂,本节和大家来看一下感知机的基本原理和Python实现。
感知机原理
假设输入x表示为任意实例的特征向量,输出y={+1,-1}为实例的类别。感知机定义由输入到输出的映射函数如下:
其中sign符号函数为:
w和b为感知机模型参数,也是感知机要学习的东西。w和b构成的线性方程wx+b=0极为线性分离超平面。
假设数据是线性可分的,当然有且仅在数据线性可分的情况下,感知机才能奏效。感知机模型简单,但这也是其缺陷之一。所谓线性可分,也即对于任何输入和输出数据都存在某个线性超平面wx+b=0能够将数据集中的正实例点和负实例点完全正确的划分到超平面两侧,这样数据集就是线性可分的。
感知机的训练目标就是找到这个线性可分的超平面。为此,定义感知机模型损失函数如下:
要优化这个损失函数,可采用梯度下降法对参数进行更新以最小化损失函数。计算损失函数关于参数w和b的梯度如下:
由上可知完整的感知机算法包括参数初始化、对每个数据点判断其是否误分,如果误分,则按照梯度下降法更新超平面参数,直至没有误分类点。
以上便是感知机算法的基本原理。当然这里说的感知机仅限于单层的感知机模型,仅适用于线性可分的情况。对于线性不可分的情形,笔者将在后续的神经网络和感知机两讲详细介绍。
感知机算法实现
完整的感知机算法包括参数初始化、模型主体、参数优化等部分,我们便可以按照这个思路来实现感知机算法。在正式写模型之前,我们先用sklearn来准备一下示例数据。
# 导入相关库
import pandas as pd
import numpy as np
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
# 导入iris数据集
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['label'] = iris.target
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
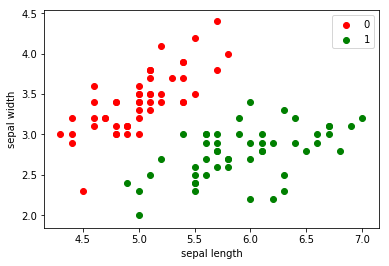
# 绘制散点图
plt.scatter(df[:50]['sepal length'], df[:50]['sepal width'], c='red', label='0')
plt.scatter(df[50:100]['sepal length'], df[50:100]['sepal width'], c='green', label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend();# 取两列数据并将并将标签转化为1/-1
data = np.array(df.iloc[:100, [0, 1, -1]])
X, y = data[:,:-1], data[:,-1]
y = np.array([1 if i == 1 else -1 for i in y])下面正式开始模型部分。先定义一个参数初始化函数:
# 定义参数初始化函数
def initilize_with_zeros(dim):
w = np.zeros(dim)
b = 0.0
return w, b然后定义sign符号函数:
# 定义sign符号函数
def sign(x, w, b):
return np.dot(x,w)+b最后定义模型训练和优化部分:
# 定义感知机训练函数
def train(X_train, y_train, learning_rate):
# 参数初始化
w, b = initilize_with_zeros(X_train.shape[1])
# 初始化误分类
is_wrong = False
while not is_wrong:
wrong_count = 0
for i in range(len(X_train)):
X = X_train[i]
y = y_train[i]
# 如果存在误分类点
# 更新参数
# 直到没有误分类点
if y * sign(X, w, b) <= 0:
w = w + learning_rate*np.dot(y, X)
b = b + learning_rate*y
wrong_count += 1
if wrong_count == 0:
is_wrong = True
print('There is no missclassification!')
# 保存更新后的参数
params = {
'w': w,
'b': b
}
return params对示例数据进行训练:
params = train(X, y, 0.01)
params最后对训练结果进行可视化,绘制模型的决策边界:
x_points = np.linspace(4, 7, 10)
y_hat = -(params['w'][0]*x_points + params['b'])/params['w'][1]
plt.plot(x_points, y_hat)
plt.plot(data[:50, 0], data[:50, 1], color='red', label='0')
plt.plot(data[50:100, 0], data[50:100, 1], color='green', label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()最后,我们也可以建一个perceptron类来方便调用。对上述代码进行整理:
class Perceptron:
def __init__(self):
pass
def sign(self, x, w, b):
return np.dot(x, w) + b
def train(self, X_train, y_train, learning_rate):
# 参数初始化
w, b = self.initilize_with_zeros(X_train.shape[1])
# 初始化误分类
is_wrong = False
while not is_wrong:
wrong_count = 0
for i in range(len(X_train)):
X = X_train[i]
y = y_train[i]
# 如果存在误分类点
# 更新参数
# 直到没有误分类点
if y * self.sign(X, w, b) <= 0:
w = w + learning_rate*np.dot(y, X)
b = b + learning_rate*y
wrong_count += 1
if wrong_count == 0:
is_wrong = True
print('There is no missclassification!')
# 保存更新后的参数
params = {
'w': w,
'b': b
}
return params