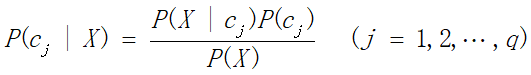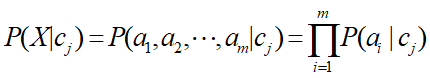朴素贝叶斯分类（NBC）的Python实现（离散）

贝叶斯分类简介

贝叶斯分类基于贝叶斯定理，贝叶斯定理是由18世纪概率论和决策论的早起研究者Thomas Bayes发明的，故用其名字命名为贝叶斯定理。基于贝叶斯理论的贝叶斯分类方法是一种具有最小错误率与最小风险的研究不确定性的推理方法。不确定性常用贝叶斯概率来表示，它是一种主观概率。
公式：

P(Cj|x)：条件x下事件Cj发生的概率；
P(x|Cj)：发生事件Cj时处于条件x下的概率；
P(Cj)：事件Cj发生的概率；
P(x)：条件x产生的概率。

朴素贝叶斯分类

在贝叶斯学习方法中实用性最高的一种是朴素贝叶斯分类方法。
朴素贝叶斯分类是一种十分简单的分类算法，叫它朴素贝叶斯分类是因为这种方法的思想真的很朴素，朴素贝叶斯的思想基础是这样的：对于给出的待分类项，求解在此项出现的条件下各个类别出现的概率，哪个最大，就认为此待分类项属于哪个类别。

朴素贝叶斯前提

类条件独立性假设：组成数据库的各个属性对于给定类的取值必须是相互独立的，也就说，任何属性的取值不依赖于其他属性。

公式

编程

从Excel中读取数据

'''
读取Excel数据
输入：文件名
输出：数据列表，数据名
'''
def excel_table_byindex(file,colnameindex=0,by_index=0):
    data = xlrd.open_workbook(file)#获取Excel数据
    table = data.sheet_by_index(by_index)#使用sheet_by_name获取sheet页名叫用户表的sheet对象数据
    colnames= table.row_values(colnameindex)#获取行数下标为0也就是第一行Excel中第一行的所有的数据值
    nrows = table.nrows #获得所有的有效行数
    list_table = []#总体思路是把Excel中数据以字典的形式存在字符串中一个字典当成一个列表元素
    for rownum in range(1,nrows):
        row =table.row_values(rownum)#获取所有行数每一行的数据值
        if row:
            app= {}#主要以{'name': 'zhangsan', 'password': 12324.0}，至于字典中有多少元素主要看有多少列
            for i in range(0,len(colnames)):#在这个Excel中，列所在的行有两个数据，所以没循环一行就以这两个数据为键，行数的值为键的值，保存在一个字典里
                app [colnames[i]] = row[i]
            list_table.append(app)
    return list_table,colnames

计算事件Cj发生的概率

'''
分解数据
输入：数据列表，数据名，预测变量数
输出：条件变量矩阵，决策变量矩阵，条件变量名，决策变量名，数据矩阵
'''
def sample_matrix(list_table,colnames,diction_num=1):#diction_num决策变量个数
    diction_name=colnames[-diction_num:len(colnames)]
    condition_name=colnames[0:-diction_num]
    list_decision=[]
    for i in range(0,len(list_table)):
        list_decision.append(list(list_table[i].values()))
    matrix=np.array(list_decision)
    matrix_decision=matrix[:,-diction_num:len(colnames)]
    matrix_condition=matrix[:,0:-diction_num]
    return matrix_condition,matrix_decision,condition_name,diction_name,matrix
'''
分解数据
输入：数据矩阵，决策变量矩阵，决策变量名
输出：决策变量字典，根据决策分类的列表
'''    
def possible_weight(matrix,matrix_decision,diction_name):
    M,N=np.shape(matrix_decision)
    dic_decision={}
    list_classify_dec=[]
    for i in range(M):
        a=''
        for j in range(N):
            if type(matrix_decision[i][j])==np.str_:  #全部大写
                matrix_decision[i][j]=matrix_decision[i][j].upper()
            a=a+(diction_name[j])+'='+matrix_decision[i][j]+','
        b=list(dic_decision)#字典
        a_cla_new=list(matrix[i])
        if a not in b:
            dic_decision[a]=1
            list_classify_dec.append([a_cla_new])
        else:
            c=b.index(a)
            dic_decision[a]=dic_decision[a]+1
            list_classify_dec[c].append(a_cla_new)
    for i in dic_decision:
        dic_decision[i]=dic_decision[i]/M
    return dic_decision,list_classify_dec

对新的条件计算每个事件发生的概率

'''
预测
输入：新的数据，根据决策分类的列表，条件变量名，决策变量字典
输出：概率
'''
def simple_predict(new,list_classify_dec,condition_name,dic_decision):
    n=len(dic_decision)
    p=np.ones([n,1])
    dic=list(dic_decision.values())
    for i in range(n):
        for k in condition_name[1:]:
            a=0
            for j in range(len(list_classify_dec[i])):
                if new[k] in list_classify_dec[i][j]:
                    a=a+1
            a=a/len(list_classify_dec[i])
            p[i]=p[i]*a
        p[i]=p[i]*dic[i]%相乘
    return p

预测

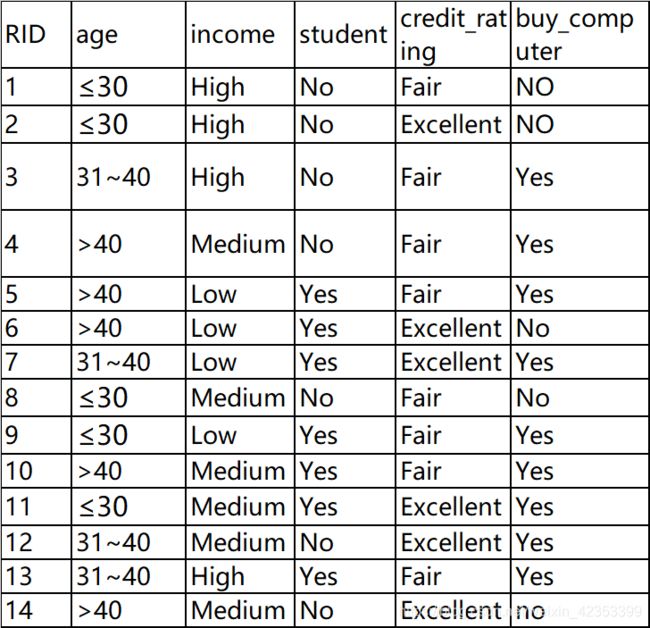
list_table,colnames=excel_table_byindex(r'D:\coures\智能信息\buyComputer_classify.xlsx')
matrix_condition,matrix_decision,condition_name,diction_name,matrix=sample_matrix(list_table,colnames)
dic_decision,list_classify_dec=possible_weight(matrix,matrix_decision,diction_name)

new={'age':'≤30','income':'Medium','student':'Yes','credit_rating':'Fair'}
p=simple_predict(new,list_classify_dec,condition_name,dic_decision)

p=p.tolist()
p_max=max(p)
p_index=p.index(p_max)
p_predict=list(dic_decision)[p_index]
print('预测结果：'+p_predict+' 概率：'+str(p_max))

运行结果

使用的数据

总代码

    import xlrd
    import numpy as np
    '''
    读取Excel数据
    输入：文件名
    输出：数据列表，数据名
    '''
    def excel_table_byindex(file,colnameindex=0,by_index=0):
        data = xlrd.open_workbook(file)#获取Excel数据
        table = data.sheet_by_index(by_index)#使用sheet_by_name获取sheet页名叫用户表的sheet对象数据
        colnames= table.row_values(colnameindex)#获取行数下标为0也就是第一行Excel中第一行的所有的数据值
        nrows = table.nrows #获得所有的有效行数
        list_table = []#总体思路是把Excel中数据以字典的形式存在字符串中一个字典当成一个列表元素
        for rownum in range(1,nrows):
            row =table.row_values(rownum)#获取所有行数每一行的数据值
            if row:
                app= {}#主要以{'name': 'zhangsan', 'password': 12324.0}，至于字典中有多少元素主要看有多少列
                for i in range(0,len(colnames)):#在这个Excel中，列所在的行有两个数据，所以没循环一行就以这两个数据为键，行数的值为键的值，保存在一个字典里
                    app [colnames[i]] = row[i]
                list_table.append(app)
        return list_table,colnames
    '''
    分解数据
    输入：数据列表，数据名，预测变量数
    输出：条件变量矩阵，决策变量矩阵，条件变量名，决策变量名，数据矩阵
    '''
    def sample_matrix(list_table,colnames,diction_num=1):#diction_num决策变量个数
        diction_name=colnames[-diction_num:len(colnames)]
        condition_name=colnames[0:-diction_num]
        list_decision=[]
        for i in range(0,len(list_table)):
            list_decision.append(list(list_table[i].values()))
        matrix=np.array(list_decision)
        matrix_decision=matrix[:,-diction_num:len(colnames)]
        matrix_condition=matrix[:,0:-diction_num]
        return matrix_condition,matrix_decision,condition_name,diction_name,matrix
    '''
    分解数据
    输入：数据矩阵，决策变量矩阵，决策变量名
    输出：决策变量字典，根据决策分类的列表
    '''    
    def possible_weight(matrix,matrix_decision,diction_name):
        M,N=np.shape(matrix_decision)
        dic_decision={}
        list_classify_dec=[]
        for i in range(M):
            a=''
            for j in range(N):
                if type(matrix_decision[i][j])==np.str_:  #全部大写
                    matrix_decision[i][j]=matrix_decision[i][j].upper()
                a=a+(diction_name[j])+'='+matrix_decision[i][j]+','
            b=list(dic_decision)#字典
            a_cla_new=list(matrix[i])
            if a not in b:
                dic_decision[a]=1
                list_classify_dec.append([a_cla_new])
            else:
                c=b.index(a)
                dic_decision[a]=dic_decision[a]+1
                list_classify_dec[c].append(a_cla_new)
        for i in dic_decision:
            dic_decision[i]=dic_decision[i]/M
        return dic_decision,list_classify_dec
    '''
    预测
    输入：新的数据，根据决策分类的列表，条件变量名，决策变量字典
    输出：概率
    '''
    def simple_predict(new,list_classify_dec,condition_name,dic_decision):
        n=len(dic_decision)
        p=np.ones([n,1])
        dic=list(dic_decision.values())
        for i in range(n):
            for k in condition_name[1:]:
            #for k in range(1:m+1):
                a=0
                for j in range(len(list_classify_dec[i])):
                    if new[k] in list_classify_dec[i][j]:
                        a=a+1
                a=a/len(list_classify_dec[i])
                p[i]=p[i]*a
            p[i]=p[i]*dic[i]
        return p
    
    
    list_table,colnames=excel_table_byindex(r'D:\coures\智能信息\buyComputer_classify.xlsx')
    matrix_condition,matrix_decision,condition_name,diction_name,matrix=sample_matrix(list_table,colnames)
    dic_decision,list_classify_dec=possible_weight(matrix,matrix_decision,diction_name)
    
    new={'age':'≤30','income':'Medium','student':'Yes','credit_rating':'Fair'}
    p=simple_predict(new,list_classify_dec,condition_name,dic_decision)
    
    p=p.tolist()
    p_max=max(p)
    p_index=p.index(p_max)
    p_predict=list(dic_decision)[p_index]
    print('预测结果：'+p_predict+' 概率：'+str(p_max))