数据结构与算法：排序专题

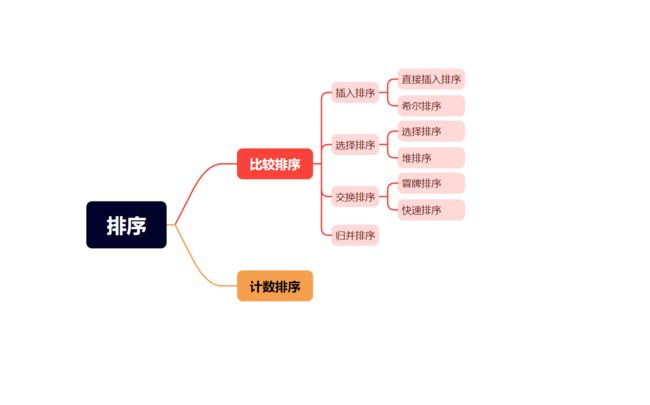
思维导图：

0.计数排序

void CountSort(int* a, int n)
{
	int min = a[0];
	int max = a[0];
	for (int i = 0; i < n; i++)
	{
		if (a[i] < min)
			min = a[i];
		if (a[i] > max)
			max = a[i];
	}
	int gap = max - min + 1;
	int* countarr = (int*)malloc(sizeof(int) * gap);
	memset(countarr, 0, sizeof(int) * gap);
	for (int i = 0; i < n; i++)
	{
		countarr[a[i] - min]++;
	}
	int j = 0;
	for (int i = 0; i < gap; i++)
	{
		if (countarr[i])
		{
			while (countarr[i]--)
			{
				a[j++] = i;
			}
		}
	}
	free(countarr);
}

思想：1.遍历原数组找出最大最小值 

2.根据最大最小值确定所开数组大小

3.再次遍历原数组，在countarr相应位置进行计数，类似哈希4.遍历countarr数组，遇到不为0的数给原数组赋值，原数组即有序

1.冒泡排序

void BubbleSort(int* a, int n)
{
	for (int i = 0; i < n - 1; i++)
	{
		int flag = 0;
		for (int j = 0; j < n - 1 - i; j++)
		{
			if (a[j] > a[j + 1])
			{
				swap(&a[j], &a[j + 1]);
				flag = 1;
			}
		}
		if (flag == 0)//这一趟没有任何交换，结束排序
		{
			return;
		}
	}
}

思想：最简单的排序，每一次将最大的数放到最后即可 

2.直接插入排序

void InsertSort(int* a, int n)
{
	for (int i = 0; i < n - 1; i++)
	{
		int end = i;
		int tmp = a[i + 1];
		while (end >= 0)
		{
			if (tmp < a[end])
			{
				a[end + 1] = a[end];
				end--;
			}
			else
				break;
		}
		a[end + 1] = tmp;
	}
}

 类似扑克牌排序，从第一张牌开始，每摸到一张牌放到合适的位置，牌始终有序

数组的第一个元素可以直接视为有序，拿起第二个元素，如果第二个元素第一个元素小，就将第一个元素往后移，那么前两个元素有序。之后每次将新元素拿起，进行类似的插入即可

3.选择排序

void SelectSort(int* a, int n)
{
	int begin = 0;
	int end = n - 1;//限制需要排序的区间
	while (begin < end)
	{
		int maxi = begin;
		int mini = begin;
		for (int i = begin; i <= end; i++)//遍历限制范围内的数组
		{
			if (a[i] > a[maxi])
				maxi = i;
			if (a[i] < a[mini])
				mini = i;
		}
		//将最小值放在begin位置，最大值放在end位置
		//如果最大值在begin，那么第一次交换最大值将换到最小值的位置
		
		swap(&a[begin], &a[mini]);
		if (maxi == begin)
		{
			maxi = mini;
		}
		swap(&a[end], &a[maxi]);
		begin++;
		end--;
	}
}

 思想：每次将最大值放在后面，最小值放在前面

4.希尔排序

void ShellSort(int* a, int n)
{
	int gap = n;
	while (gap > 1)
	{
		gap = gap / 3 + 1;
		for (int i = 0; i + gap < n; i++)
		{
			int end = i;
			int tmp = a[i + gap];
			while (end >= 0)
			{
				if (tmp < a[end])
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				else
					break;
			}
			a[end + gap] = tmp;
		}
	}
}

在插入排序的基础上增加了预排序，每间隔gap为一组进行排序，循环到最后gap等于1，就是一次插入排序

5.堆排序

 

void AdjustDown(int* a, int n, int parent)
{
	int child = 2 * parent + 1;
	while (child < n)
	{
		if (child + 1 < n && a[child + 1] > a[child])
		{
			child++;
		}
		if (a[parent] < a[child])
		{
			swap(&a[parent], &a[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
			break;
	}
}
void AdjustUp(int* a, int child)
{
	int parent = (child - 1) / 2;
	while (child)
	{
		if (a[child] > a[parent])
		{
			swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
			break;
	}
}
void HeapSort(int* a, int n)
{
	//建堆
	//向上调整建堆
	/*for (int i = 1; i < n; i++)
	{
		AdjustUp(a, i);
	}*/
	//向下调整建堆
	for (int i = (n - 1 - 1) / 2; i >= 0; i++)
	{
		AdjustDown(a, n, i);
	}
	//调堆
	//建大堆，排升序；建小堆，排降序
	int end = n - 1;
	while (end)
	{
		swap(&a[0], &a[end]);
		AdjustDown(a, end, 0);
		end--;
	}
}

 思想将在堆中进行讲解

6.归并排序

递归型

void _MergeSort(int* a, int begin, int end, int* tmp)
{
	if (begin == end)
		return;
	int mid = (begin + end) / 2;
	_MergeSort(a, begin, mid, tmp);
	_MergeSort(a, mid+1, end, tmp);
	int begin1 = begin, end1 = mid;
	int begin2 = mid+1, end2 = end;
	int j=begin;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] < a[begin2])
		{
			tmp[j++] = a[begin1++];
		}
		else
		{
			tmp[j++] = a[begin2++];
		}
	}
	while (begin1 <= end1)
	{
		tmp[j++] = a[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[j++] = a[begin2++];
	}
	memcpy(a + begin, tmp + begin, sizeof(int)*(end-begin+1));
}
void MergeSort(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	_MergeSort(a, 0, n - 1, tmp);
	free(tmp);
}

非递归型 

void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	int gap = 1;
	while (gap < n)
	{
		for (int i = 0; i < n; i+=2*gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;
			int j = i;
			if (begin2 >= n)
			{
				break;
			}
			if (end2 >= n)
			{
				end2 = n - 1;
			}
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				else
				{
					tmp[j++] = a[begin2++];
				}
			}
			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}
			memcpy(a + i, tmp + i, sizeof(int) * (end2 - i));
		}
		gap *= 2;
	}
	free(tmp);
}

7.快速排序

普通快排

//hoare
int PartSort1(int* a, int begin, int end)
{
	int keyi = begin;//keyi在左，先动右指针
	while (begin < end)
	{
		while (begin < end && a[end] >= a[keyi])
		{
			end--;
		}
		while (begin < end && a[begin] <= a[keyi])
		{
			begin++;
		}
		swap(&a[begin], &a[end]);
	}
	swap(&a[keyi], &a[begin]);
	return begin;
}
//挖坑
int PartSort2(int* a, int begin, int end)
{
	int hole = begin;
	while (begin < end)
	{
		while (begin < end && a[end] >= a[hole])
		{
			end--;
		}
		swap(&a[end], &a[hole]);
		hole = end;
		while (begin < end && a[begin] <= a[hole])
		{
			begin++;
		}
		swap(&a[begin], &a[hole]);
		hole = begin;
	}
	return hole;
}
//前后指针
int PartSort3(int* a, int begin, int end)
{
	int key = a[begin];
	int prev = begin;
	int cur = begin + 1;
	while (cur <= end)
	{
		if (a[cur] <= key)
		{
			swap(&a[cur], &a[++prev]);
		}
		cur++;
	}
	swap(&a[begin], &a[prev]);
	return prev;

}
void QuickSort(int* a, int n)//可以有其他参数设置方法，这里跟其他排序函数参数保持一致
{
	int begin = 0;
	int end = n - 1;
	if (begin >= end)
		return;
	int keyi = PartSort3(a, begin, end);
	QuickSort(a, keyi);
	QuickSort(a + keyi + 1, end - keyi);
}

 针对重复数据的三路划分

//三路划分
void QuickSort2(int* a, int begin,int end)
{
	if (begin >= end)
		return;
	int key = a[begin];
	int left = begin;
	int right = end;
	int cur = begin + 1;
	while (cur <= right)
	{
		if (a[cur] < key)
		{
			swap(&a[cur], &a[left]);
			cur++;
			left++;
		}
		else if (a[cur] > key)
		{
			swap(&a[cur], &a[right]);
			right--;
		}
		else
		{
			cur++;
		}
	}
	QuickSort2(a, begin, left-1);
	QuickSort2(a, right + 1, end);
}

 不会因递归导致栈溢出的非递归快排

//非递归快排
void QuickSortNonR(int* a, int n)
{
	Stack s;
	StackInit(&s);
	int begin = 0;
	int end = n - 1;
	StackPush(&s, begin);
	StackPush(&s, end);
	while (!StackEmpty(&s))
	{
		end = StackTop(&s);
		StackPop(&s);
		begin = StackTop(&s);
		StackPop(&s);
		int keyi = PartSort1(a, begin, end);
		if (keyi+1 < end)
		{
			StackPush(&s, keyi+1);
			StackPush(&s, end);
		}
		if (begin < keyi - 1)
		{
			StackPush(&s, begin);
			StackPush(&s, keyi-1);
		}
	}
	StackDestroy(&s);
}