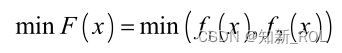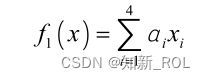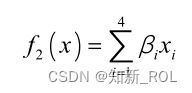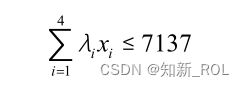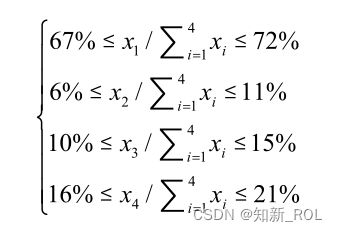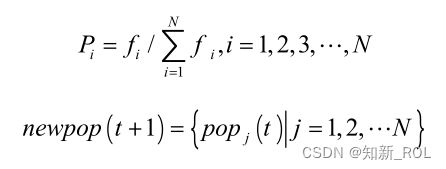2023华为杯数学建模D题第三问-碳排放路径优化(能源消费结构调整的多目标优化模型构建详细过程+模型假设(可复制))
1.碳排放约束下(人为干预按时碳达峰与碳中和的基准情景)能源消费结构多目标优化模型构建
1.1基本假设
本文的模型设计主要基于以下几个基本假设:
(1)能源消费结构调整的根本驱动要素,是对投资耗费的最小化和对环境污染处理费用的最小化。
(2)受科学技术进步制约,假定各燃料种类的来源方式不变,则单位种类能源的碳排放系数恒定不变。
(3)依据 BP神经网络模型的能源消费预测结果,取其在特定范围内波动值为最佳优化区域,以实现能源结构优化。
(4)各行业间不存在技术差异,能源利用效率的改变反映在能源消费结构的调整中,忽视科技、管理等因素对能源利用效率的影响。
(5)在低碳转型背景下,模型目标是在保持经济平稳增长的前提下,能源消费总量达到最少,同时让碳排放量最低。
(6)碳排放量是环境污染指标的最主要考虑因素。
1.2总体目标函数
多目标优化问题(multiobjective optimization problem,MOP)是一门迅速发展起来的学科,是最优化的一个重要分支,它是智能计算(Intelligent Computing)领域的一个重要研究方向。起源于对许多实际复杂体系的设计、构造与规划。它重点研究在某种意义下多个数值目标的同时最优化问题[81]。多目标综合优化提问是和传统的单目标综合优化提问相比,在特定情况中,当要求实现多种总体目标时,由于很易产生总体目标之间的内在矛盾,某个总体目标的优势往往是以其他总体目标优劣为代价,所以很难产生唯一最优预测解,取而代之的是在他们之间进行调和与折衷处理,使总体的目标尽量的达到最大化,也是探究在某种意义下多数量总体目标的共同最大化提问。它和单目标优化问题的根本差别就是,它的求解目标绝非惟一,只是面临着一套由多个帕累托求解(Pareto Optimal)所构成的最优预测求解集,整体中的所有元素均为 Pareto解,也称为非劣解[82]。而过多的非劣解是无法直接应用的,所以在求解时就是要寻找一个最终解。但过多的非劣解是无法进行实际应用的,所以在求解时候就是要寻求一种最终解法。过多目标规划的好处,就是非常强调对可行方法的替代性以及对所要实现目标的选择性。而且,多个目标计划还可以同时兼顾几个相互产生矛盾的目标,并能够通过决策者对公司几个目标间不同相对价值的选择,解决公司几个不同优先级目标的优化问题。就这样,可以在解决公司产品规划、生产区域选择、能源计划、交通运输等问题时,多目标规划法得到了广泛的应用。在实际生活中,优化设计工作从总体上都体现着最佳效果、最低成本这二条基本的设计优化原则,但在这一原则基础上很多问题都是由彼此矛盾和相互影响的几个目标所构成,这就使得决策变动相对困难。大多数系统的多目标优化技术的基本思路都是把多个项目问题简单化,再转换为单个项目进行解决。求解的一般步骤是首先将问题调整分析,之后采取单目标的求解模型寻找答案,最后将求得最优解作为非单一目标问题的答案。常用的多目标综合设计优化方式有:加权求和法(Weighted SumMethod)、ε-约束法(ε-Constraint Method)、加权度量方法(Weighted Metric Method)。本节采用加权求和法对能源消费结构进行多目标优化,构建目标函数如下:
经过加权处理后的目标函数形式为:
上式中, F x 代表的是总目标函数, ![]() (i=1,2i) 代表的则是不同目标函数的权重,总目标函数中包括了能源消费成本最小和环境污染治理费用最小这两个目标。
(i=1,2i) 代表的则是不同目标函数的权重,总目标函数中包括了能源消费成本最小和环境污染治理费用最小这两个目标。
(1)能源消费成本量。能源消费量最小是追求能源效益最优的重要方面,设其目标函数为:
(2)环境污染治理费用最小。减少碳排放量可以转化为最小化环境治理费用的问题。目标函数可以表示为:
1.3模型约束条件
(1)能源消费总量约束。根据题目中的结果显示,
非化石能源消费比重是指非化石能源消费量与能源消费量的比值,提高非化石能源消费比重是降低单位能耗二氧化碳排放量的根本和关键。
《意见》中明确指出,到2025年非化石能源消费比重达到20%左右;到2030年非化石能源消费比重达到25%左右;到2060年非化石能源消费比重超过80%。为了实现非化石能源消费比重超过80%的目标,非化石能源发电比重和电力消费比重均应达到90%。提高非化石能源消费比重的必要条件是提高非化石能源发电占比,需要由新能源发电、脱碳火电和包含储能在内的新型电网等能源生产部门完成;而充分条件是提高非化石能源消费比重,需要由工业消费部门、建筑消费部门、交通消费部门、居民生活消费和农林消费部门等能源消费部门完成。
因此本文中根据2023年中国研究生数学建模竞赛题思路及模型 | 知新的官方博客对能源消费总量的预测,按照上下浮动 5%的水平同时设置上限和下限
(2)碳排放总量约束。
假设2、2060年生态碳汇的碳消纳量为基期碳排放量的10%;
假设3、2060年工程碳汇或碳交易的碳消纳量为基期碳排放量10%。
![]() i为不同能源的碳排放系数,得到式(5-11)约束条件
i为不同能源的碳排放系数,得到式(5-11)约束条件
(3)能源消费结构约束。
碳排放量核算模型与问题二中预测模型相一致(即在多情景条件约束下,区域与各部门能源消费量、能源消费品种及其碳排放量预测方法相一致)。
(4)非负约束
相关分析方法主要是研究变量间是不是具有某种相互依存关系,而结合到本课题就是运用 SPSS统计分析软件,观察能源行业固定资产投资费用和环境污染处理费用与各能源消费量之间的相关程度。对 5个自变量:煤炭、石油、天然气、水电及其他能发电的消费量、能源消费总量与 2个因变量在 SPSS软件的支持下,
1.4优化方案设计
1)节能优先
在节能优先的方案中,设置能源消费成本权重大于环境污染处理费用权重,即 ![]() (i=1,2),( 0.75,0.25) 。能源消费成本代表的是在生产活动中实际消费的各种能源消费成本的总和,本文中用固定资产投资表征能源消费成本。为了使能源效率达到最高,能耗强度降低,达到节能要求,就要使得能源固定资产投资得到充分利用。
(i=1,2),( 0.75,0.25) 。能源消费成本代表的是在生产活动中实际消费的各种能源消费成本的总和,本文中用固定资产投资表征能源消费成本。为了使能源效率达到最高,能耗强度降低,达到节能要求,就要使得能源固定资产投资得到充分利用。
(2)减排优先
在减排优先的方案中,设置能源污染治理费用权重大于能源消费成本权重,即 ![]() (i=1,2)( 0.25,0.75) 。能源污染治理费用与碳排放息息相关,为了降低碳排放,优化生态环境,减少能源消费污染物,可以通过设置能源污染治理费用最小来实现能源
(i=1,2)( 0.25,0.75) 。能源污染治理费用与碳排放息息相关,为了降低碳排放,优化生态环境,减少能源消费污染物,可以通过设置能源污染治理费用最小来实现能源
减排的优化。
(3)节能与减排并重
在综合节能和减排方案中,对能源污染治理费用和能源消费成本分别设置相同权重,即 ![]() (i=1,2),( 0.5,0.5) 。能源消费结构的优化使能源消费结构趋于合理化发展,终极目的是为达到在能源消费和生态环境之间保持均衡,而平衡节能与减排之间的关系能很好的反映能源消费结构优化的效果。
(i=1,2),( 0.5,0.5) 。能源消费结构的优化使能源消费结构趋于合理化发展,终极目的是为达到在能源消费和生态环境之间保持均衡,而平衡节能与减排之间的关系能很好的反映能源消费结构优化的效果。
1.5多目标优化结果
1)遗传算法(Genetic Algorithm,GA)
1975年,美国纽约 MicHigan学院的 J.H.Holland博士在研究学习时注意到,机器学习不但能够利用对一个生物体的适应性来实现,并且还能够利用对一个群体的许多进化适应性来进行实现,于是 KennethDeJong把这些计算用于处理优化问题。因为遗传算法的计算中并不包括所有待解决所具有的问题形态,它是通过改变人类基因组的配置来进行对问题的总体优化的,所以属于自下而上的优选方案。人的天然演化过程也是进化论流程,这个进化论流程主要出现在染料体上,天然筛选使适应性值较好的染料体比一些适应性值较不好的染料体具有更多的增殖机会,天然变异使子代染料体不同于父代染料体。遗传算法,就是是为了模仿在大自然中生物发展的遗传机制和天然筛选流程所提出的[84]。遗传算法是一个群体式运算,该方法可以以生物学族群中的任何一个为对象,三种重要控制算子为筛选、交错和突变,也因此形成了所说的遗传操作法(geneticoperation),利用对生物学遗传与进化流程中筛选、交错与突变等机制的仿真,来实现对难题最佳预测解的自适应性搜索过程方法,实质上有所不同于常规的多目标与整体风险和解计算技术,不要求对各子任务的权重设定,比传统的多目标优化方式作用更突出,已被人类普遍地运用在组合优选、机器学习、信息加工、自适应控制,以及人力健康等应用领域。也是现代有关生物学智能算法中的核心技术之一。由于能源消费结构优化问题配置的多目标性,利用原有的规划方式往往不得而解好这类提问,但多目标遗传算法却具有运算简单易行等优点,甚至可以在一个运行中就得到优化问题的类似 Pareto最优解集[85],于是本节使用遗传算法对的能源消费结构多目标优化模型进行了计算。
遗传算法的过程包括编码、交叉、变异、选择等,它们能够相互独立参与进化。具
体操作步骤如下:
Step1:编码和产生初始群体。
选择以二进制编码方法,把问题的可行解从解空间中转移到由遗传算法所能控制的
空间结构中,并随机得到 N个串结构数据, N个串结构数据构成一个群体,当作起始
节点开始迭代。设有进化代数计算器 0t ,设置最大进化代数T ,随机生成 N个个体成
为初始群 P0
Step2:计算适应度值。
适应度函数表明了个体的优劣性,需要根据具体的问题计算群体 pop t 中各个个体
的适应度值。
Step3:选择操作。
将选择算子作用于群体,根据 Step2中所得适应度函数值计算概率大小 iP ,随机选取适应度高的个体遗传到下一代群体中,构成一个新种群 newpop进行下一步操作。
Step4:交叉操作。将交叉算子作用于群体,交叉操作以概率 cP随机选取个体在随机
生成的位置上进行交叉,得到群体 crosspop (t+1)。
Step5:变异操作。将变异算子作用于群体,以变异概率 mP随机选取个体进行变异,
得到新的群体 mutpop (t +1)
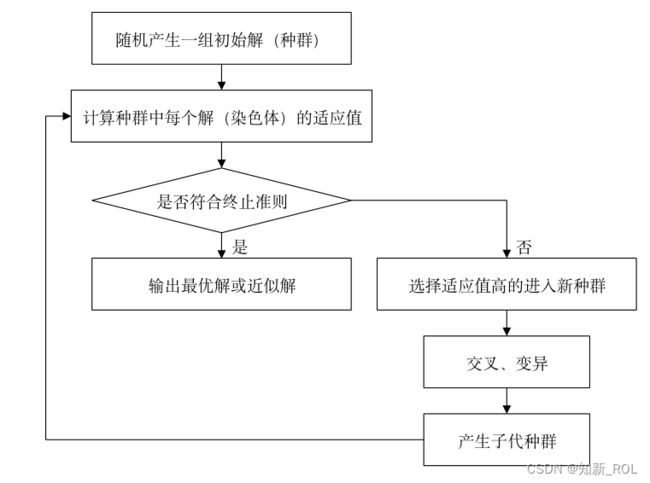
在进行了最大的迭代代数后,算法停止执行。遗传算法的计算流程图,如图 5-1所
示。
结果分析
在对遗传算法做了基本的学习了解之后,调用 MATLAB软件中遗传算法工具箱,
按照上述步骤利用的历史数据,通过优化模型对能源消费结构进行优化。
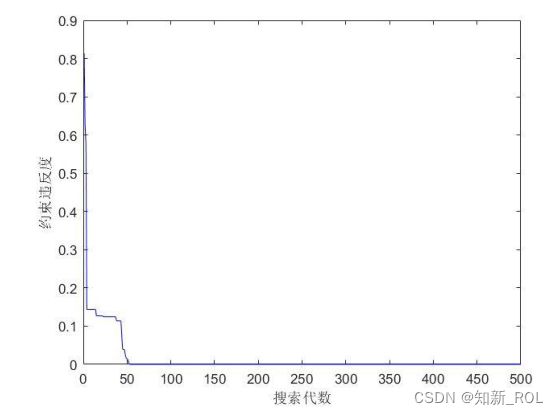
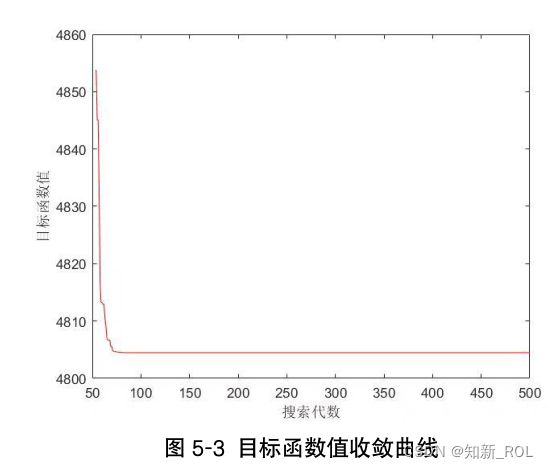
其中,设置交叉 cP概率为 0.9变异概率 mP为 0.02,取迭代次数为 500,得到如下的约
束违反度曲线和收敛曲线。
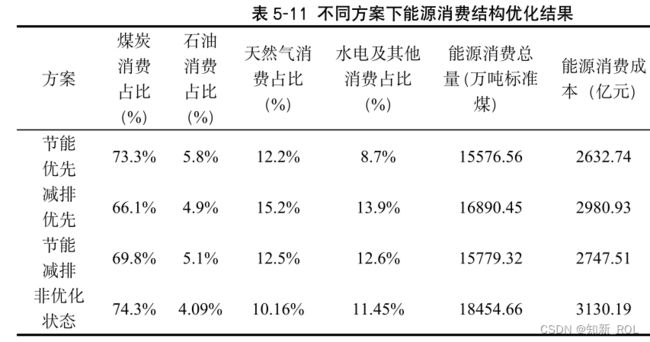
图 5-2的约束违反度曲线在迭代次数达到第 50次的时候就已经降低到 0,意味着找到了满足约束的解。图 5-3的目标函数值的收敛曲线在迭代的过程中趋势逐渐下降,说明优化效果较好。图 5-2和图 5-3均为节能优先的方案中,运算的效果呈现,在减排优先和节能减排方案中效果类似,故不做赘述。不同方案下的优化结果如表 5-11所
表 5-11中呈现的是三种不同的优化方案下,未来的能源消费结构与能源消费总量。由表可知,节能优先的方案下,在目标函数中设置能源消费成本权重最大,也就是此方案中,在一定的碳排放和能源消费总量等约束条件上,力求能源消费成本达到最小。优化结果中,煤炭消费占比为 73.3%,在所有能源消费占比重遥遥领先,天然气消费占比次之,符合能源消费结构状况,但是没有有效的控制煤炭消费量。减排优先的方案下,煤炭消费占比优化到了 66.1%,是三种方案中最能有效控制煤炭消费的优化方案,同时天然气消费和水电消费在该情况下的消费比重均有上升。节能减排方案下,不仅有效的减少量能源污染治理费用,而且煤炭消费占比较非优化状态下有所降低,为 69.8%。石油、天然气和水电及其他消费占比都略有提高,小幅度的、平均的优。
相关参考代码如下:
% 遗传算法参数
population_size = 100; % 种群大小
num_generations = 50; % 迭代代数
mutation_rate = 0.1; % 变异率
% 初始化种群
gene_length = 10; % 基因长度
population = randi([0, 1], population_size, gene_length);
% 适应度函数:示例目标函数 f(x) = x^2
fitness = @(x) sum(x.^2, 2);
% 主循环
for generation = 1:num_generations
% 计算适应度
fitness_values = fitness(population);
% 选择操作
selected_population = zeros(population_size, gene_length);
for i = 1:population_size
parent1 = select_individual(population, fitness_values);
parent2 = select_individual(population, fitness_values);
[child1, child2] = crossover(parent1, parent2);
selected_population(i, :) = mutate(child1, mutation_rate);
end
population = selected_population;
end
% 找到最优解
best_individual = population(1, :);
best_fitness = fitness(best_individual);
fprintf('最优解: ');
disp(best_individual);
fprintf('最优值: %f\n', best_fitness);
% 选择操作:轮盘赌选择法
function selected = select_individual(population, fitness_values)
total_fitness = sum(fitness_values);
r = rand * total_fitness;
current_sum = 0;
for i = 1:length(population)
current_sum = current_sum + fitness_values(i);
if current_sum >= r
selected = population(i, :);
return;
end
end
end
% 交叉操作:单点交叉
function [child1, child2] = crossover(parent1, parent2)
point = randi([1, length(parent1) - 1]);
child1 = [parent1(1:point), parent2(point + 1:end)];
child2 = [parent2(1:point), parent1(point + 1:end)];
end
% 变异操作:单点变异
function mutated = mutate(individual, mutation_rate)
mutated = individual;
for i = 1:length(individual)
if rand < mutation_rate
mutated(i) = ~mutated(i);
end
end
end