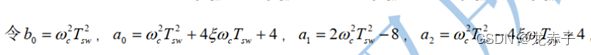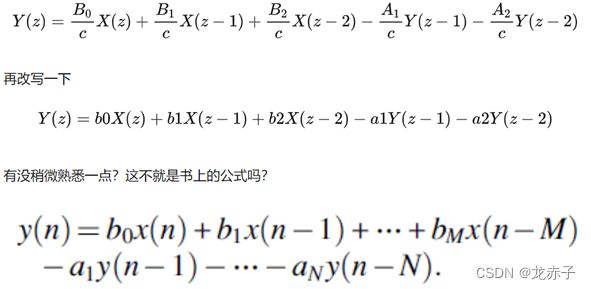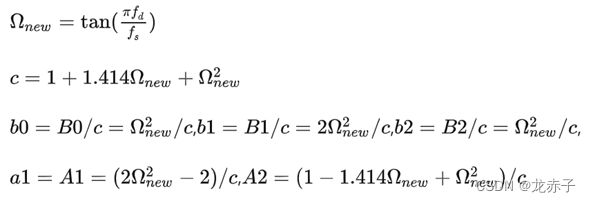关于二阶低通滤波的C代码及入门测试

目录

一 前言

二 第一份实现

三 第二份实现

四 总结

---

一 前言

低通滤波器在许多领域都有广泛的应用。博主也因为需要，最近看了看这方面的资料。因为一方面主要需求是二级低通滤波的实现，另一方面该需求只是功能中引入的一个小点，不是做这方面研究用，所以在资料的挑选上就比较苛刻，那些讲一大堆原理公式的就不太适合，有点头重脚轻。反而那些直达目标，讲如何代码实现的，是博主比较关注的。

也正因为如此，感觉网上资料比较少。而且好多资料虽然有代码，但也穿插了比较多的理论和概念，有的还需要二次转换，这种资料，很多时候就放弃了。查的东西多了，就逐渐发现，要想将复杂的事情简单化，是比较考验能力水平的。这就好比，大人给小孩子讲明白一个事情是比较难的，反过来，小孩子觉得自己讲了一件非常复杂的事情，可能在大人觉得还是比较简单的。

书越读才能越薄，必要的概念还是不能绕过去。

首先，要区分几个干扰概念：就是FIR、IIR、巴特沃斯、还有其他一些类型的参数。这里的二阶低通滤波，其实是一个比较笼统的说法。为了找到比较合适的公式，简单的了解了一下这些概念。参考知乎上的这篇文章：【滤波专题-第1篇】数字滤波器15分钟入门！——这可能是最简单的FIR有限冲激响应滤波讲解 - 知乎

简单来讲，FIR是有限冲激响应，离散化的实现中，y只与x及x的历史有关，与y的历史无关，而IIR则不同，不仅与x的历史有关，还与y的历史有关。这是区分二者的比较直接简单的方法。

后面的实现按这个方法来区分的话，是属于IIR的。

插一句：程序实现这些功能，是需要先进行离散化处理的，然后按采样点一个一个的计算。

二 第一份实现

算法的公式如下：图片来自网络，https://www.cnblogs.com/tuxinbang/p/10705443.html

离散化的推到及实现参考：https://blog.csdn.net/qq_26988431/article/details/100779047

第一份代码就是参考该博文写的。需要注意的是，这篇博文中有一个参数编码的实现弄错了，跟上面图片中对应的系数不一致。

网上找的很多代码并不能直接拿来测试，这里我把自己改写的代码直接放上来，入门的小伙伴可以直接用来测试：

#define Const_2pi       (6.283185)
#define Const_TS        (0.0001) //100us

//二阶低通滤波器
float LPF2(float xin) {
   float f= 20;
   float wc = Const_2pi * f;
   float dampingRatio = 0.707;

   float lpf2_b0 = wc*wc*Const_TS*Const_TS;
   float lpf2_a0 = 4 + 4*dampingRatio*wc*Const_TS + lpf2_b0;
   float lpf2_a1 = -8 + 2*lpf2_b0;
   //float lpf2_a2 = 4 - 4*dampingRatio*wc*Const_TS  + lpf2_a0; //原始这里应该有误
   float lpf2_a2 = lpf2_b0 + 4 - 4*dampingRatio*wc*Const_TS;

   static float lpf2_yout[3] = {0};
   static float lpf2_xin[3] = {0};

   lpf2_xin[2] = xin;
   lpf2_yout[2] = (lpf2_b0 * lpf2_xin[2] + 2*lpf2_b0 *lpf2_xin[1] + lpf2_b0 *lpf2_xin[0] -lpf2_a1 *lpf2_yout[1] - lpf2_a2*lpf2_yout[0]) / lpf2_a0;
   lpf2_xin[0] = lpf2_xin[1];
   lpf2_xin[1] = lpf2_xin[2];
   lpf2_yout[0] = lpf2_yout[1];
   lpf2_yout[1] = lpf2_yout[2];

   return lpf2_yout[2];
}

代码里，截至频率选择了20hz，阻尼比 选择了0.707. Const_TS就是转为离散化实现的时候，采样的周期。这里按10K来测试，该值就是100us，代码中要用秒单位，因此是0.0001 另一个常量2Pi就不用解释了。

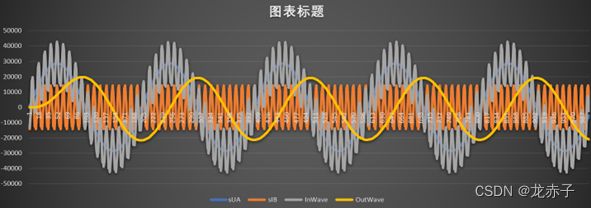
为了方便测试上述函数，构造了一个周期50hz的正弦波，另外构造了一个1Khz的噪声正弦波，将两个波形叠加起来，作为输入，看看上面的滤波代码能否正常工作。

上图中，灰色的是合成的输入，黄色的是过滤后的输出。背景中的蓝色波就是50hz的正常波，二橘色的就是模拟噪声的1khz的波

从上图来看，噪声波基本被过滤了，滤波后的频率与原始正常波看着也很接近。不知道理解是不是正确。

但是，这里幅值有明显的衰减。也不知道是什么原因，比较程序是活的，改改参数看看，将截至频率从20hz调整到50hz，过滤效果如下图：

看来应该是跟频率关系比较大。这个图就看着比较舒服了。这里也能明显的看到相位差了。

三 第二份实现

博主虽然学过信号与系统，但是早都还给老师了，所以，也不知道上面的理解对不对。另外搜索资料过程中，也发现了很多不同的实现，于是本着审慎的态度，就找了另一个实现，来相互验证下。公式差不多，如下图 图片来自飞控中的IIR二阶滤波器 - 知乎

按上面的公式，另实现了一份，代码如下：

//二阶低通滤波器
float LPF2_T2(float xin) {
   static float lpf2_yout[3] = {0};
   static float lpf2_xin[3] = {0};

   float sample_freq = 10000;
   float cutoff_freq = 100;
   float fr = sample_freq / cutoff_freq;

   float ohm = tan(PI * cutoff_freq /sample_freq);
   float c = 1 + 1.414 * ohm  + ohm * ohm;
   
   float b0 = ohm * ohm /c;
   float b1 = 2.0f * b0;
   float b2 = b0;

   float a1 = 2.0f * (ohm * ohm - 1.0f) /c;
   float a2 = (1.0f - 1.414 * ohm + ohm * ohm) / c;
   
   lpf2_xin[2] = xin;
   
   lpf2_yout[2] = b0 * lpf2_xin[2] + b1 * lpf2_xin[1] + b2 * lpf2_xin[0] - a1 * lpf2_yout[1] - a2 * lpf2_yout[0];

   lpf2_xin[0] = lpf2_xin[1];
   lpf2_xin[1] = lpf2_xin[2];
   lpf2_yout[0] = lpf2_yout[1];
   lpf2_yout[1] = lpf2_yout[2];

   return lpf2_yout[2];
}

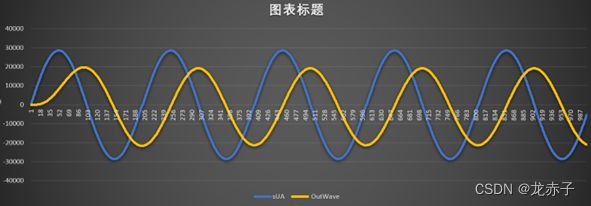
可以看到，除了参数系数的写法不一样外，其他部分跟第一份实现都是比较接近的。采样频率还是10Khz,截至频率选择了100，输入跟第一份代码一样，我们看看结果：

蓝色是50hz输入，橘色是截至频率为100hz的实现，灰色和黄色是两份实现在20hz的情况下的输出，可以看到，灰色的基本被黄色曲线盖住了，这说明两个公式实现的功能是完全一致的，这似乎也间接验证了接口的正确性。

四 总结

上面两份代码都没有做优化，其实系数在频率参数确定的情况下是固定的，因此可以提前计算好，这样可提升整体性能；另外就是，上面的实现仅供参考，博主本人也在继续学习，有问题欢迎大家指正。