基座向量施密特正交化
最近再次细细的阅读了向量施密特正交化,重新系统梳理一下
一、正交基地与向量的正交分解
二、基化成标准正交基,是什么意思
将一个向量空间中的基向量通过某种方式转化为一组标准正交基,是指将原有的基向量进行调整,使得它们满足两个条件:
- 彼此之间两两正交(即内积为零);
- 归一化(长度为1)。
这样的转换可以用来简化向量空间中的运算,使得向量的表示更加方便和直观。标准正交基在线性代数和向量空间理论中非常重要
三、原始的基向量为什么要化为标准正交基
将原始的基向量转换为标准正交基有一些重要的好处:
1. 方便计算:标准正交基的向量彼此之间两两正交,这意味着它们的内积为零。这种性质简化了向量运算的计算过程,减少了计算量和复杂度。
2. 简化表示:由于标准正交基的向量彼此正交且长度为1,使用这样的基向量表示向量时,各个基向量的系数就可以直接表示向量的分量。这使得向量的表示更加简洁和直观。
举个例子,考虑一个三维空间中的向量空间。假设原始的基向量是线性相关的(不是正交的),可能是(1, 1, 0)和(2, -1, 1)。如果我们将它们转换为标准正交基,我们可以使用Gram-Schmidt正交化过程来获得新的标准正交基。
通过Gram-Schmidt正交化过程,我们可以得到两个彼此正交的向量(1, 1, 0)和(-1, 4, 1)。这两个向量可以作为新的标准正交基。利用这两个标准正交基向量,我们可以将原始的基表示的向量(3, 2, -1)进行投影和线性组合,从而得到向量在新基下的表示。
这种转换使得向量的表示更加简单明了,计算过程也更加便捷。这是为什么将原始的基向量转换为标准正交基的一个重要原因。
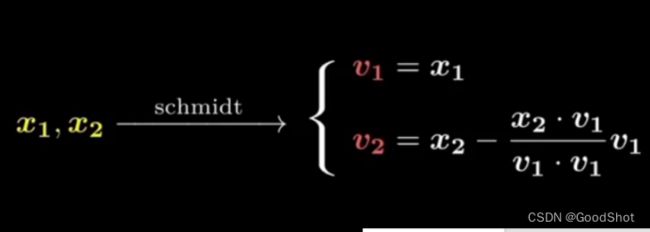
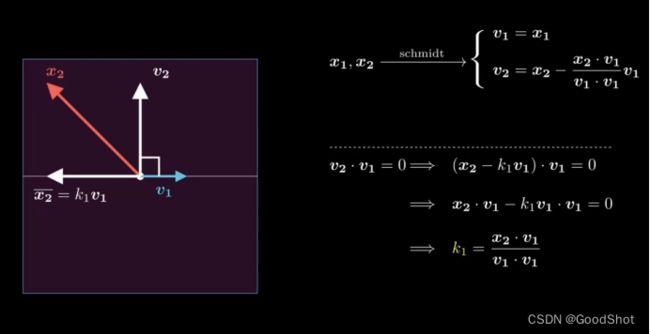
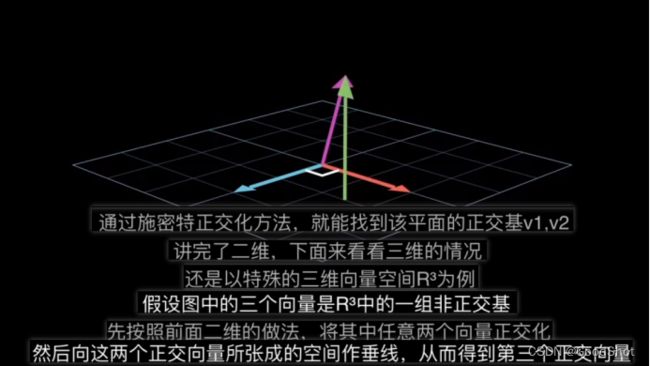
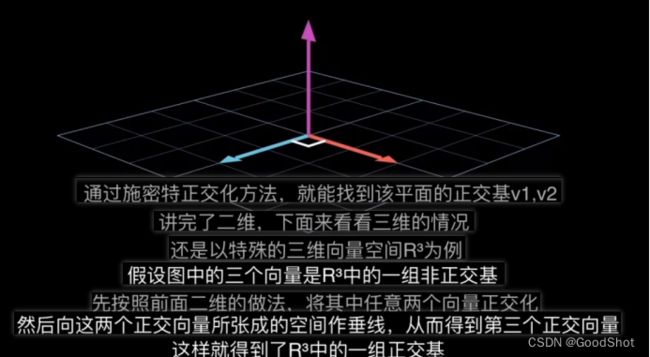
四、施密特正交化过程形象理解
五、单位正交基的转换保持向量之间的内积关系不变
施密特正交化是一种将一组线性独立的向量转化为正交的过程,同时保持原有向量所张成的子空间。这个过程不会改变原始基所张成的子空间,也就是说,通过施密特正交化得到的正交基在子空间方面与原始基是等价的。
我们可以通过一个例子来说明这个问题。假设我们有一组线性独立的向量 {v₁, v₂, v₃} 作为我们的原始基。通过施密特正交化的过程,我们可以得到一个新的正交基 {u₁, u₂, u₃}。新基中的每个向量 uₖ 都与前面的向量正交。
尽管新基中的向量彼此正交,但是在原始基中的向量组合仍然可以用新基的向量来表示。换句话说,由原始基张成的子空间仍然可以用新基的向量来表示。
数学上来说,如果一个向量 v 在原始基中可以表示为原始基向量的线性组合(v = c₁v₁ + c₂v₂ + c₃v₃),那么它也可以用新基向量来表示(v' = c₁u₁ + c₂u₂ + c₃u₃),其中 v' 和 uₖ 分别表示新基和向量。
因此,尽管施密特正交化过程中的个别向量与原始基不同,所得到的正交基在子空间方面仍然与原始基是等价的。
六、同一向量,在原始基和对应施密特转化之后的正交基中,用来表示该向量坐标是否一致
在原始基和对应施密特转化之后的正交基中,用来表示同一个向量的坐标是不一致的。原始基中的坐标与施密特转化后的正交基中的坐标不具有直接的对应关系。
在施密特正交化过程中,我们通过线性组合得到了一组正交的基向量,这使得向量的表示更加简化。由于正交基的性质,向量的坐标会发生变化。通过施密特正交化,向量在新的正交基中的表达方式可能会发生改变,即坐标值不同。
因此,在原始基和施密特转化后的正交基中,用来表示同一个向量的坐标是不一致的。这是因为施密特正交化过程会改变向量的表示形式,但维持了向量的方向和长度不变。