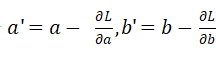神经网络基础数学原理之一----线性回归（含Tensorflow 2.x代码）

本文是关于神经网络的原理的科普文。虽然提到神经网络，不可避免到涉及到一些数学推导的内容（如偏导），但本文尽量做到对一般学历能力（高中、专、本科等）的人都能完全读懂。虽然现在tensorflow的出现，令神经网络已经变成了一套封装良好的API，对于大部分直接使用者来说，不需要深究其中的运算过程及数学原理。但多了解点原理，对问题建模，构建网络，调优，排错来说，是大有陴益的。

后面将通过一系列的文章来解释神经网络一些最基本的概念，包括输入样本(Input)，标签(Label)，神经元(neuron)，神经网络(Neuron Network)，输出函数(Output)，正向传播(Forward propagation)，反向回馈（backward propagation），损益函数(Loss Function)，激活函数(Activate Function)，梯度下降(gradient descent)，学习率（Learning rate）等。并通过对这些概念的介绍，以数学推导和代码实现的方式解释神经网络是如何解决现实生活中一个典型的分类问题。

1、线性回归

所谓的线性回归，就是在未知线性函数F(x)的确切表达式的前提下，使用另外一个近似函数f(x)来代替原函数F(x)。

例子：设有未知一元线性函数F(x)=Ax + B ，现希望找到一个近似函数f(x) ，使| F(x) - f (x) | <ε。

下面来研究如何来找这个近似函数f(x)。

首先，由于不知道具体A,B的取值，不妨先随机选择一个f(x)=ax + b，其中a,b都是随机选取。

由于拟合函数f(x)是随机选取，所以不能保证F(x)=f(x)。因此，必须抽样计算对于同一个自变量x0 ，函数F(x0),f(x0)之间的差值|F(x) - f (x)|。如果将这个差值，视为一个由原函数F(x)与近似函数f(x)组合，则可以定义出所谓的损益函数Loss（x）= |F(x) – f(x)|。

一般损益函数经常以均方差的形式出现，但为了下文的讨论方便这里直接取差值的绝对值。为了简化讨论，这里把损益函数的取绝对值操作去掉。因为在实际的运算过程中，优化常常都是从一侧进行的。所以在运算前期的某一时间段内，可以认为Loss(x)= | F(x) - f (x) | = F(x) – f(x)。

通过简单的计算可得Loss(x)= (A – a)x + (B - b)。这里把A,B当作是已知量来用。现在问题变成了如何使Loss(x)降低。

前面从计算f(x),F(x)到计算Loss(x)的过程，事实上就是神经网络的前向传播过程。在上述这段简短描述中，出现了随机训练样本x0，神经元f(x0)，标签F(x0)。如果我们把f(x0)想象成一个神经元,那么整个算法结构就是一个十分简单的只有一层且该层只有一个神经元的神经网络。其中系数a称为神经元的权重(weight),b 称为偏置(bias)。

有些朋友可能对F(x)的取值感到迷惑，认为在不知道F(x)具体表达式的情况下，不可能知道F(x)的值。但在现实生活中，我们却往往只知道答案，而不知道细节。而神经网络却能通过细节，来预测答案。

回到刚刚的问题，现在问题已经转化成求损益函数Loss(x)的最小值。在x不变的情况下，降低Loss(x)的办法，只有修正权重值a和偏置值b。将Loss视为a,b的二元函数。分别求偏导得。

下面将介绍神经网络进行参数优化的重要过程梯度下降。

由高数知识可知，当连续可导函数的导数为0，则函数达到最大/最小值。而自变量沿着偏导数的反方向移动时，导数下降得最快。因此前面求出的偏导数又称为损失函数的梯度（gradient）。既然自变量沿负梯度方向移动，会快速令导数为0，这就为神经网络优化权重和偏置提供了可行方案。因此梯度下降的过程就是不断令

的过程。

这个算法就是所谓的梯度下降算法

下面我们来验证梯度下降算法的确能令损益函数变小。

令a’=a+x0, L = Loss(a), L’=Loss(a’)则损益函数

L’=(A – a’)* x0 – B + b = (A – a - x0) * x0 – B + b

   =(A – a) * x0 – B + b – x0^2 = L - x0^2 < L

显然梯度下降算法可以有效降低损失函数。对于偏置b的讨论与a类似，把调整后的值代入原损失函数，同样可以得到损失函数减小的结论，这里就不再赘述。

上述通过计算损失函数梯度，反向调整参数的过程，就叫做反向传播过程。神经网络的训练过程就是不断地输入同一个x，计算输出，损失函数及梯度，然后反向调整网络参数的过程，至此，一个最简单的神经网络训练的流程大体就已经解释清楚了。

整个算法流程虽然已经很清晰了，但在实际运行上，梯度下降的过程却并不是一帆风顺的。最典型的情况是当A-a= x0 / 2。a 的优化无法推进。读者可自行验算，这里由于篇幅有效，不再赘述。

因此神经网络需要输入多个不同的x值，来保证优化能持续进行，以最终达到Loss < ε的原定目标。

下面是tensorflow 2.x的实现代码:

# 神经网络模拟线性函数
import tensorflow as tf
#随机初始化样本集
x = tf.Variable(tf.random.truncated_normal([100,1],dtype=tf.double,stddev=1),name="x_train")
# 目标函数y = 3 * x + 2
y = x * 3 + 2;

# 基本网络模型
class model():
    def __init__(self):
    	# 随机初始化 w 权重值
        self.w=tf.Variable(tf.random.truncated_normal([1],dtype=tf.double,stddev=1))
        # 随机初始化 b 偏置值
        self.b=tf.Variable(tf.convert_to_tensor([1],dtype=tf.double))
    # 这里当一个类型实现了特殊方法__call__,该类的实例就变成了可调用的类型, 对象名() 等价于 对象名.__call__() ,
    # 有时候可以简化对象的调用,让对象变成可调用的对象, 实现__call__即可
    def __call__(self,x):
        return x*self.w+self.b

# 计算均方差
def loss(pre,true):
    return tf.reduce_mean(tf.square(pre-true))

# 训练
def train(model,inputs,outputs,learning_rate):
    with tf.GradientTape() as t:
    	# 求误差
        current_loss=loss(model(inputs),outputs)
        # 求w 的偏导,求b的偏导
        dw,db=t.gradient(current_loss,[model.w,model.b])
        # w沿负梯度移动，更新w
        model.w.assign_sub(dw*learning_rate)
        # b沿负梯度移动, 更新b
        model.b.assign_sub(db*learning_rate)

# 初始化模型
model=model()
# 循环2000次
for epoch in range(2000):
	# 计算损失，用于打印
    current_loss=loss(model(x),y)
    # 训练
    train(model,x,y,learning_rate=0.05)
    # 打印
print('Epoch %d  W=%f b=%d, loss=%e' %(epoch,model.w.numpy(),model.b.numpy(),current_loss))

 

打印结果：

...

Epoch 1997  W=3.000000 b=2, loss=1.301374e-29

Epoch 1998  W=3.000000 b=2, loss=1.301374e-29

Epoch 1999  W=3.000000 b=2, loss=1.301374e-29

由于受限于机器的硬件性能，不可能将无穷多的自变量值输入到神经网络中运算，所以网络训练有所谓批次（batch ）的概念。主流的神经网络算法框架（目前主要指Tensorflow）还提供了随机梯度下降算法来进一步优化参数优化速度。所谓随机梯度下降算法就是舍弃一定的精度，只随机选样本集中的部分样本作为训练输入，从而提高整个神经网络的性能。另外，参数在沿梯度下降的时候,实际是按λ倍的梯度值来进行的，其中0<λ<1,λ称为学习率（learning rate）。加入学习率是为了避免参数因梯度过大而左右摇摆，提高算法的效率与精度。