刷题常用算法模板(持续更新)
目录
-
- 1、二分查找
- 2、线段树
- 3、树状数组
- 4、差分数组
- 5、前缀树
- 6、并查集
- 7、AC自动机
- 8、Morris遍历
- 9、二叉树非递归遍历
- 10、KMP
- 11、Manacher
- 12、快速选择 bfprt
- 13、滑动窗口
- 14、加强堆
- 15、有序表
- 16、单调栈
- 17、数位DP
- 18、快速幂
1、二分查找
需求:在一个有序数组中,快速查询某一个值。时间复杂度O(logN),空间复杂度O(1)。
举个例子:
int[] arr = {1, 2, 2, 2, 4, 5};
int target = 2;
以下二分查找的写法就是返回 >=2 的最左位置的下标。也就是返回 1下标。
切记:在数组中查询不到target时,返回的是无效的下标,上层调用时记得加判断。
新的需求:请返回 >=target 中的最右的下标。就只需调用 >= target + 1的函数,然后返回的下标再-1即可。当然上层调用时,还是需要判断返回的下标值是否合法。
LeetCode练习题
二分查找常见的三种写法,注意区分各自的不同之处。
// 1、闭区间写法。返回 >=target 的最左位置的下标
private static int lowerBound1(int[] arr, int target) {
int l = 0;
int r = arr.length - 1;
while (l <= r) { // 闭区间
int mid = (l + r) >> 1;
if (arr[mid] < target) { // [mid + 1, right]
l = mid + 1;
} else { // [left, mid - 1]
r = mid - 1;
}
}
// 循环停止条件:l = r + 1。返回其一即可
return l;
}
// 2、开区间写法。返回 >=target 的最左位置的下标
private static int lowerBound2(int[] arr, int target) {
int l = -1;
int r = arr.length;
while (l + 1 < r) { // 开区间
int mid = (l + r) >> 1;
if (arr[mid] < target) { // (mid, right)
l = mid;
} else { // (left, mid)
r = mid;
}
}
return r; // 循环停止条件:left+1=right,返回其一即可
}
// 3、左闭右开区间写法。返回 >=target 的最左位置的下标
private static int lowerBound3(int[] arr, int target) {
int l = 0;
int r = arr.length;
while (l < r) { // 左闭右开
int mid = (l + r) >> 1;
if (arr[mid] < target) { // [mid + 1, right)
l = mid + 1;
} else { // [left, mid)
r = mid;
}
}
// 循环停止条件:l == r。返回其一即可
return r;
}
2、线段树
需求:为了快速的对数组某一段连续的区间进行增删改查操作。时间复杂度O(logN),空间复杂度O(N)。
关键字:范围更新。
写法并不统一,这里的写法是 5个数组搭配。(有的写法是4个数组,省去update数组。在change数组上使用Integer类型,若某个位置的元素 == null,说明是没有修改的情况,这里就不多赘述)。
切记:为了方便计算,线段树中的tree数组,是用于存储原数组的数据,但这里的tree数组0下标的空间省去不用,从1下标位置开始存储的。并且为了出现一些例外的情况,导致在后续递归调用时,会出现数组越界异常,所以change、lazy、sum、update这四个数组的存储空间要 开辟 (tree.length * 4)倍的长度。
下文代码的查询操作(query)写的是 某个区间的累加和。也可根据题目意思更改query的代码,将sum数组改成其他含义的数组表示,例如如下题目:
LeetCode练习题。这道题就是计算 某个区间的最大高度,将sum数组改写成hight数组即可。
private static class SegmentTree {
private int[] tree; // 从下标1位置开始填入
private int[] change; // 存储修改的值
private int[] lazy; // 懒更新数组
private int[] sum; // 存储某个范围内的数据总和,根据需求而定。
private boolean[] update; // 记录相应下标位置是否需要进行更新
private int length;
public SegmentTree(int[] arr) {
this.length = arr.length + 1;
tree = new int[length];
for (int i = 1; i < length; i++) { // 将数据填充到tree中
this.tree[i] = arr[i - 1];
}
change = new int[length << 2];
lazy = new int[length << 2];
sum = new int[length << 2];
update = new boolean[length << 2];
}
// 对sum数组进行初始化,也就是计算出相应区间的总和
public void build(int l, int r, int rt) {
if (l == r) {
sum[rt] = tree[l];
return;
}
int mid = (r + l) / 2;
build(l, mid, rt << 1); // 递归左子树
build(mid + 1, r, rt << 1 | 1); // 递归右子树
pushUp(rt); // 两边汇总
}
/**
* 在L和R范围内,添加某个数
* @param L 需要修改数据的范围的左边界
* @param R 需要修改数据的范围的右边界
* @param l 当前递归的左边界
* @param r 当前递归的右边界
* @param num 添加的值
* @param rt lazy数组的下标(树的根节点)
*/
public void add(int L, int R, int num, int l, int r, int rt) {
if (L <= l && R >= r) { // 当前递归范围,超出了修改数据的范围,可以懒
sum[rt] += (r - l + 1) * num; // 总和
lazy[rt] += num;
return;
}
// 不能懒的情况,取中位数进行递归
int mid = (r + l) / 2;
// 先将上次lazy数组留下的数据向下分发之后,再进行调用
// mid - l + 1是左子树的节点数
// r - mid 是右子树的节点数
pushDown(rt, mid - l + 1, r - mid);
if (L <= mid) { // 递归左子树
add(L, R, num, l, mid, rt << 1);
}
if (R > mid) { // 递归右子树
add(L, R, num, mid + 1, r, rt << 1 | 1);
}
pushUp(rt); // 等左右子树递归完,再做汇总
}
/**
* L、R范围内更新值
* @param L 待更新范围左边界(固定值)
* @param R 待更新范围右边界(固定值)
* @param num 更新值
* @param l 当前递归的左边界
* @param r 当前递归的右边界
* @param rt change数组的下标(树的根节点)
*/
public void update(int L, int R, int num, int l, int r, int rt) {
if (L <= l && R >= r) { // 当前递归范围超过了待更新的范围
update[rt] = true;
change[rt] = num;
sum[rt] = (r - l + 1) * num; // 重新计算sum
lazy[rt] = 0; // lazy数组对应的位置要归0
return;
}
// 没有懒到,取中位数,往下递归
int mid = l + ((r - l) >> 1);
// 先往下分发数据,然后才是递归调用
pushDown(rt, mid - l + 1, r - mid);
if (L <= mid) {
update(L, R, num, l, mid, rt << 1);
}
if (R > mid) {
update(L, R, num, mid + 1, r, rt << 1 | 1);
}
pushUp(rt); // 汇总数据
}
// 查询L和R范围内的sum总和
public long query(int L, int R, int l, int r, int rt) {
if (L <= l && R >= r) {
return sum[rt];
}
int mid = l + ((r - l) >> 1);
pushDown(rt, mid - l + 1, r - mid); // 往下分发
long ans = 0;
if (L <= mid) {
ans += query(L, R, l, mid, rt << 1);
}
if (R > mid) {
ans += query(L, R, mid + 1, r, rt << 1 | 1);
}
return ans;
}
// lazy数组向下分发数据
private void pushDown(int rt, int leftChildSum, int rightChildSum) {
// 用于add方法
if (lazy[rt] != 0) { // 懒数组的数据不为0,说明要往下分发
sum[rt << 1] += lazy[rt] * leftChildSum; //左子树的总和
sum[rt << 1 | 1] += lazy[rt] * rightChildSum; // 右子树的总和
// 更新左右子树的lazy数组
lazy[rt << 1] += lazy[rt];
lazy[rt << 1 | 1] += lazy[rt];
lazy[rt] = 0; // 当然位置的lazy值归0
}
// 用于update方法
if (update[rt]) { // 是否需要更新的情况
// 标志update数组,表示需要更新
update[rt << 1] = true;
update[rt << 1 | 1] = true;
// 更新左右子树的change值
change[rt << 1] = change[rt];
change[rt << 1 | 1] = change[rt];
// 更新左右子树的sum总和
sum[rt << 1] = change[rt] * leftChildSum;
sum[rt << 1 | 1] = change[rt] * rightChildSum;
// 左右子树的lazy数组都需要归0
lazy[rt << 1] = 0;
lazy[rt << 1 | 1] = 0;
update[rt] = false; // 当前位置的数据分发完了,就改回false
}
}
// 汇总数据
private void pushUp(int rt) {
sum[rt] = sum[rt << 1] + sum[rt << 1 | 1]; // 将左右子树的数据进行汇总
}
}
3、树状数组
需求:会频繁的更新数组中某一个位置的数据,但又需要快速的计算某个区间的累加和问题。时间复杂度O(logN),空间复杂度O(N)。
树状数组,也称为IndexTree,算是线段树的另一种形式。也是实现数组区间内的快速增删改查。与线段树的区别是 能够实现单点更新,比线段树更轻量化。还有一个好处就是,可以很轻易的改写成二维的形式。
关键词:单点更新,快速计算某一个段区间的累加和。
IndexTree有三个函数,add、update、query。
query查询的是 0 ~ index位置的累加和。
比如要查询 3 ~ 5位置的累加和问题,就能转换为 求 0 ~ 5的累加和 减去 0~2的累计和。
// 一维。上层调用时的下标,还是从0开始。只是进入IndexTree后,自己手动+1
public class IndexTree {
public int[] nums; // 原数组
public int[] tree; // 累加和数组
public int length; // 0下标的空间省去不用
public IndexTree(int N) {
this.length = N + 1;
tree = new int[this.length];
nums = new int[this.length];
}
/**
* 在index位置插入val值。index从1开始
* @param val 待插入的值
* @param index 数组下标
*/
public void add(int val, int index) {
index += 1;
nums[index] += val;
for (int i = index; i < length; i += (i & -i)) { // index位置插入值,会影响后面位置的计算
tree[i] += val;
}
}
/**
* 更新index位置的值
* @param val 更新的值
* @param index 下标
*/
public void update(int val, int index) {
index += 1;
int num = val - nums[index]; // 差值
nums[index] = val;
for (int i = index; i < length; i += (i & -i)) {
tree[i] += num; // 累加上 差值
}
}
/**
* 返回1下标~index下标的累加和
* @param index 下标
* @return 返回累加和
*/
public int query(int index) {
index += 1;
int ans = 0;
for (int i = index; i > 0; i -= (i & -i)) {
ans += tree[i];
}
return ans;
}
}
// 二维。上层调用时,还是从下标0开始,进入IndexTree后,下标自动+1
public class Code02_IndexTree2D {
private int[][] nums;
private int[][] tree;
private int N; // 行数
private int M; // 列数
public Code02_IndexTree2D(int[][] matrix) {
if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
return;
}
N = matrix.length + 1;
M = matrix[0].length + 1;
nums = new int[N][M];
tree = new int[N][M];
for (int i = 0; i < N - 1; i++) {
for (int j = 0; j < M - 1; j++) {
update(matrix[i][j], i, j);
}
}
}
// row,col位置 更新值 val。 row,col的范围在 0~N-1,或者0~M-1
public void update(int val, int row, int col) {
if (N == 0 || M == 0 || row < 0 || col < 0 || row > N - 1 || col > M - 1) {
return;
}
row += 1;
col += 1;
int num = val - nums[row][col]; // 差值
nums[row][col] = val;
for (int i = row; i < N; i++) {
for (int j = col + 1; j < M; j++) {
tree[i][j] += num;
}
}
}
// 返回 row,col 到左上角的矩形的累加和
private int sum(int row, int col) {
if (row < 0 || col < 0 || row > N - 1 || col > M - 1) {
return 0;
}
row += 1;
col += 1;
int ans = 0;
for (int i = row; i > 0; i -= (i & -i)) {
for (int j = col; j > 0; j -= (j & -j)) {
ans += tree[i][j];
}
}
return ans;
}
/**
* @param row1 左上角
* @param col1 左上角
* @param row2 右下角
* @param col2 右下角
* @return 返回左上角 到 右下角 围成的矩形的累加和
*/
public int sumRegion(int row1, int col1, int row2, int col2) {
if (N == 0 || M == 0) {
return 0;
}
return sum(row2, col2) - sum(row2, col1 - 1) - sum(row1, col2 - 1) + sum(row1 - 1, col1 - 1);
}
}
4、差分数组
需求:快速对数组的某一段连续区间进行加减法操作。时间复杂度O(N),空间复杂度O(N)。
/**
* 差分数组
* @param arr 原数组
* @param option 操作数组,有3个参数。
*/
private static void fastUpdateOfArray(int[] arr, int[][] option) {
/*
option数组有三个参数:
option[i][0] = 带更新范围的左边界
option[i][1] = 带更新范围的右边界
option[i][2] = 新值
*/
int N = arr.length;
// 1、由原数组 反推 差分数组
int[] diff = new int[N + 1]; // 多开一个位置的空间
diff[0] = arr[0];
for (int i = 1; i < N; i++) {
diff[i] = arr[i] - arr[i - 1];
}
// 2、将新值 更新到差分数组
for (int[] pos : option) {
int left = pos[0]; // 左边界
int right = pos[1]; // 右边界
int val = pos[2]; // 新值
diff[left] += val; // 左边界 + val
diff[right + 1] -= val; // 右边界的后一个位置 -val
}
// 3、再对diff数组求前缀和数组,就是更新过后的arr数组的值
arr[0] = diff[0];
for (int i = 1; i < N; i++) {
arr[i] = diff[i] + arr[i - 1];
}
}
5、前缀树
需求:给定一组字符串,将这些字符串插入前缀树中,后续可以查询某个子串,在前缀数中有多少个字符串是以这个子串开头的。
应用:后续的AC自动机,就是前缀树 + KMP写的。
public class TrieTree {
private final TrieNode root;
public TrieTree() {
// 根节点不指向任何字符,root节点的pass值就是整颗前缀数有多少字符串
root = new TrieNode();
}
private static class TrieNode {
public int pass; //途径的数量
public int end; // 某个单词的总数量
// 这里的HashMap中的键值,也可以是其他的。这里只是以大小写字母的情况写的
public HashMap<Character, TrieNode> map; //保存下一节点的地址
public TrieNode() {
map = new HashMap<>();
}
}
public void add(String word) {
if (word == null) {
return;
}
char[] array = word.toCharArray();
TrieNode node = root;
node.pass++;
for (char ch : array) {
if (!node.map.containsKey(ch)) {
node.map.put(ch, new TrieNode());
}
node = node.map.get(ch);
node.pass++;
}
node.end++;
}
public int search(String word) {
if (word == null) {
return 0;
}
char[] array = word.toCharArray();
TrieNode node = root;
for (char ch : array) {
if (!node.map.containsKey(ch)) {
return 0;
}
node = node.map.get(ch); //拿到下一节点
}
return node.end; //返回最终的end值
}
/**
* @param word 以word为前缀的字符串
* @return 返回以word为前缀的字符串的数量
*/
public int prefixNumber(String word) {
if (word == null) {
return 0;
}
char[] array = word.toCharArray();
TrieNode node = root;
for (char ch : array) {
if (!node.map.containsKey(ch)) {
return 0;
}
node = node.map.get(ch); //拿到下一节点
}
return node.pass;
}
public boolean delete(String word) {
if (word != null && search(word) != 0) {
char[] array = word.toCharArray();
TrieNode node = root;
node.pass--;
for (char ch : array) {
if (--node.map.get(ch).pass == 0) {
//pass值为0,所以从该节点一下的所有子树,都将不存在,所以直接全部回收即可
//C++ 的,需要遍历所有子树,调用析构函数
node.map.remove(ch);
return true;
}
node = node.map.get(ch);
}
node.end--;
return true;
}
return false;
}
}
6、并查集
需求:快速的判断某两个节点是否属于同一集合。时间复杂度O(1),空间复杂度O(N)。
并查集的写法有很多种,理解其思想,方可改写。还有的是使用数组来写的并查集,比如使用Integer[] 数组,若 某个位置的元素 == null,说明这个位置的元素还没有进来过。
1、初始化时,每个节点的父节点都是指向自己本身的
2、find时,要进行路径压缩。这也是时间复杂度O(1)的来源
3、sizeMap,是在union时,让“小的集合 挂在 大的集合下面”,有一定的优化效果。但大多数OJ时,这个可以不用写,一般都是能过的。
// 包装Node节点的 + sizeMap优化版本。
public class UnionSet {
private HashMap<Node, Node> fatherMap; //key表示当前这个数据,value表示这个数据的代表(父亲)是谁
private HashMap<Node, Integer> sizeMap; //表示当前这个组(集合)的大小
public UnionSet() { //构造方法
fatherMap = new HashMap<>();
sizeMap = new HashMap<>();
}
private static class Node {
public int val;
public Node next;
public Node(int val) {
this.val = val;
}
}
//初始化并查集
public void makeSet(List<Node> list) {
if (list == null) {
return;
}
fatherMap.clear();
sizeMap.clear(); //先将表清空
//遍历list,把每一个节点,都放入哈希表中
for (Node node : list) {
fatherMap.put(node, node); //第一个参数是节点本身,第二个参数就是这个组的代表
sizeMap.put(node, 1); //第一个参数是这个组的代表,第二个参数是大小
}
}
//判断是不是同一个组
public boolean isSameSet(Node node1, Node node2) {
if (node1 == null || node2 == null) {
return false;
}
return findFather(node1) == findFather(node2); //查找各自的代表节点,看是不是同一个。
}
//查找代表节点,并做路径压缩
private Node findFather(Node node) {
if (node == null) {
return null;
}
//查找代表节点
Stack<Node> path = new Stack<>(); //存储沿途的节点
while (node != fatherMap.get(node)) { //代表节点不是自己本身,就继续查找
path.push(node);
node = fatherMap.get(node);
}
//路径压缩
while (!path.isEmpty()) {
Node tmp = path.pop();
fatherMap.put(tmp, node); //此时的node,就是这个组的代表节点
}
return node;
}
//合并操作
public void union(Node node1, Node node2) {
if (node1 == null || node2 == null) {
return;
}
int node1Size = sizeMap.get(node1);
int node2Size = sizeMap.get(node2); //分别得到两个节点所在组的大小
Node node1Father = fatherMap.get(node1);
Node node2Father = fatherMap.get(node2); //分别拿到两个节点的代表节点
if (node1Father != node2Father) { //两个节点,不在同一个组,就合并
if (node1Size < node2Size) { //node1 挂在 node2
fatherMap.put(node1Father, node2Father);
sizeMap.put(node2Father, node1Size + node2Size); //新的组,大小是原来两个组的和
sizeMap.remove(node1Father); //小组的数据,就不需要了,删除
} else { //node2 挂在 node1
//跟上面操作类似
fatherMap.put(node2Father, node1Father);
sizeMap.put(node1Father, node1Size + node2Size);
sizeMap.remove(node1Father);
}
}
}
}
// 稍微简单一点的并查集写法。初始化操作就写在find函数里
// 值得注意的是,这里并没有包装Node节点,只是单纯的使用Integer
// 有的题目,有可能出现两个相同的数字,导致并查集里的索引出现错乱的情况
private class UnionSet {
private HashMap<Integer, Integer> father; // 7、AC自动机
需求:给定一篇文章,和一组敏感词汇,问 这一篇文章中有哪些敏感词汇。
思路:先对这些敏感词汇建立一颗前缀树,然后在前缀树上写KMP。
核心要点:fail指针,其实就是对于到KMP中的那个next数组,将那边的思想搬运过来,如下的build()函数,可能就更好理解了。根节点的fail=null,根节点的下一级子节点的fail指向根节点,这一句话就对于了KMP中的next数组的初始化状态:next[0] = -1, next[1] = 0。都是为了在匹配失败的时候,往前跳转。
public class Code03_AC1 {
public static void main(String[] args) {
ACAutomation ac = new ACAutomation();
ac.insert("dhe");
ac.insert("he");
ac.insert("abcdheks");
// 设置fail指针
ac.build();
List<String> contains = ac.containWords("abcdhekskdjfafhasldkflskdjhwqaeruv");
for (String word : contains) {
System.out.println(word);
}
}
// 前缀树节点
private static class Node {
public String end; // 以当前节点结尾,这条线路的字符串
public boolean endUse; // 标记是否已经找到过这个敏感词
public Node fail; // fail指针,匹配失败时,往上找最佳的前缀字符串的开始节点
public Node[] nexts; // 下级节点,可以是数组,也可以是哈希表的形式,根据数据类型来定
public Node() {
this.end = null;
this.endUse = false;
this.fail = null;
this.nexts = new Node[26]; // 假设是26个小写字母
}
}
private static class ACAutomation {
private Node root;
public ACAutomation() {
this.root = new Node();
}
public void insert(String str) {
char[] chars = str.toCharArray();
Node cur = root;
for (int i = 0; i < chars.length; i++) {
int num = chars[i] - 'a';
if (cur.nexts[num] == null) {
cur.nexts[num] = new Node();
}
cur = cur.nexts[num];
}
cur.end = str; // 尾结点,记录这条线路的字符串
}
// 连接所有节点的fail指针 ----使用BFS
// 根节点的fail是null,根节点的直接下级节点的fail都是 指向 根节点
// fail=null和fail指向根节点,也就直接对应了KMP中next数组的前两个位置就是-1、0的情况
public void build() {
Queue<Node> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()) { // BFS
Node cur = queue.poll();
// 遍历nexts数组
for (int i = 0; i < 26; i++) { // 处理他的孩子节点
if (cur.nexts[i] != null) { // 有孩子节点的情况
cur.nexts[i].fail = root; // 先指向root。后续如果有其他情况,再修改
Node curFail = cur.fail;
while (curFail != null) {
if (curFail.nexts[i] != null) { // 父节点的fail指向的节点 也有走向i位置的路,就连接
cur.nexts[i].fail = curFail.nexts[i];
break; // 连上之后,直接跳出了
}
curFail = curFail.fail; // 再往下一个fail节点跳转
}
queue.add(cur.nexts[i]); // 当前节点入队列
}
}
}
}
// 查询content文章中的敏感词
public List<String> containWords(String content) {
if (content == null || content.length() == 0) {
return new ArrayList<>();
}
Node cur = root;
int length = content.length();
List<String> ans = new ArrayList<>();
for (int i = 0; i < length; i++) {
int index = content.charAt(i) - 'a';
// 没有走向index的路,但是cur又不是根节点的情况,继续沿着fail走
while (cur.nexts[index] == null && cur != root) {
cur = cur.fail;
}
cur = cur.nexts[index] != null? cur.nexts[index] : root;
// 现在cur要么是走到了下级节点,要么就还是在root位置
// 以当前cur节点跑一遍fail指针,尝试搜集沿途的敏感词
Node follow = cur;
while (follow != root) {
if (follow.endUse) { // 说明当前节点已经搜集过敏感词了,无需再次搜集
break;
}
// 不同的需求,可修改一下代码
if(follow.end != null) {
ans.add(follow.end);
follow.endUse = true;
}
follow = follow.fail;
}
}
return ans;
}
}
}
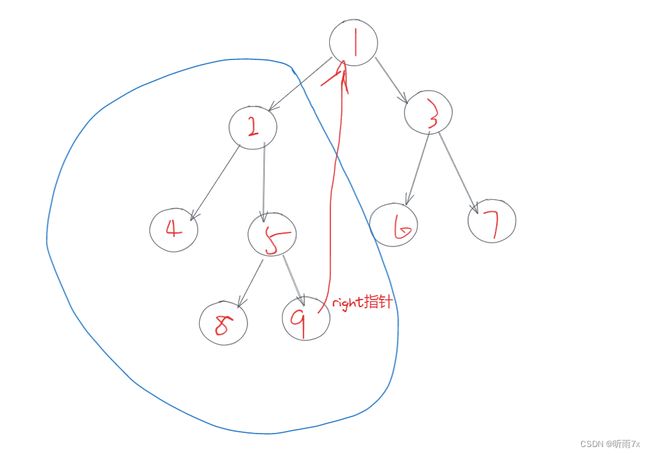
8、Morris遍历
需求:以时间复杂度O(N), 空间复杂度O(1) 的要求,遍历二叉树。
核心要点:将某一颗左子树中,最右侧的节点的right指针,指向根节点。如下图所示:
//可以在Morris的基础之上,改写前序、中序、后序遍历
// 前序是第一来到的节点就打印
// 中序是第二次来到的节点就打印
// 后序是在第二次来到mostRight时,往上逆序打印。需要反转right指针的走向,才能做到空间O(1)
private static class TreeNode {
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode(int val) {
this.val = val;
}
}
private static void morris(TreeNode node) {
if (node == null) {
return;
}
TreeNode cur = node;
while(cur != null) {
TreeNode mostRight = cur.left; // 左子树
if(mostRight != null) { // 左子树不为空
// 尽可能的往右子树走
while(mostRight.right != null && mostRight.right != cur) {
mostRight = mostRight.right;
}
// 循环停下来,就是走到了最右侧的节点
if (mostRight.right == null) {
// 第一次来到这个节点,right指针连上cur
// 1、做你想做的操作,比如打印节点
// 2、继续往左子树走
cur = cur.left;
continue;
} else {
// 第二次来到这个节点,断开right指针连 cur
mostRight.right = null;
}
} else { // 左子树为空
}
cur = cur.right;
}
}
9、二叉树非递归遍历
两种实现方式:1、Morris遍历;2、使用栈模拟
// TreeNode节点
private static class TreeNode {
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode(int val) {
this.val = val;
}
}
// 1、Morris 前序遍历
// 前序遍历二叉树
public static void morrisPreOrder(TreeNode root) {
if (root == null) {
return;
}
// 找到当前节点的左子树上 最右的节点,并将该节点的右指针指向当前cur节点
TreeNode mostRight = null;
TreeNode cur = root;
while (cur != null) { // 只要cur没有遍历完,循环就继续
mostRight = cur.left;
if (mostRight != null) {
while (mostRight.right != null && mostRight.right != cur) { // 往最右节点靠拢
mostRight = mostRight.right;
}
// 停下来时,有两种情况
// 1是右指针为null,说明是第一次遍历到当前节点
// 2是右指针指向cur,说明是第二次遍历到当前节点
if (mostRight.right == null) {
mostRight.right = cur; // 指向cur节点
System.out.print(cur.val + " ");
cur = cur.left;
continue; // 继续往左子树走
} else {
mostRight.right = null;
}
} else { // 往右子树走之前,先打印当前cur的值
System.out.print(cur.val + " ");
}
cur = cur.right; // 转向右子树
}
System.out.println();
}
// 1、Morris 中序遍历
// 中序遍历二叉树
public static void morrisInOrder(TreeNode root) {
if (root == null) {
return;
}
TreeNode cur = root;
TreeNode mostRight = null;
while (cur != null) {
mostRight = cur.left;
if (mostRight != null) {
// 往最右节点靠拢
while(mostRight.right != null && mostRight.right != cur) {
mostRight = mostRight.right;
}
if (mostRight.right == null) { // 第1次来到cur节点
mostRight.right = cur;
cur = cur.left; // 继续往左子树走
continue;
} else { // 第2次来到cur节点
mostRight.right = null;
System.out.print(cur.val + " ");
}
} else {
System.out.print(cur.val + " ");
}
cur = cur.right; // 往右子树转
}
System.out.println();
}
// 1、Morris 后序遍历
// 后序遍历二叉树
public static void morrisPostOrder(TreeNode root) {
if (root == null) {
return;
}
TreeNode cur = root;
TreeNode mostRight = null;
while (cur != null) {
mostRight = cur.left;
if (mostRight != null) {
while (mostRight.right != null && mostRight.right != cur) {
mostRight = mostRight.right;
}
if (mostRight.right == null) {
mostRight.right = cur;
cur = cur.left;
continue;
} else { // 第2次来到cur节点,此时就打印cur.left节点,最靠右这一列的节点
mostRight.right = null;
printList(cur.left);
}
}
cur = cur.right; // 往右子树转
}
printList(root); // 最后打印根节点最靠右的一列
System.out.println();
}
private static void printList(TreeNode left) {
// 首先反转最靠右的一列,从下面往上打印
TreeNode node = reverseList(left);
TreeNode cur = node;
while (cur != null) {
System.out.print(cur.val + " ");
cur = cur.right;
}
reverseList(node); // 再反转回来
}
// 反转TreeNode最右这一列节点
public static TreeNode reverseList(TreeNode node) {
TreeNode pre = null;
TreeNode next = null;
while (node != null) {
next = node.right;
node.right = pre;
pre = node;
node = next;
}
return pre;
}
// 2、用栈模拟
// 非递归前序遍历
public static void preOrderNoRecursion(TreeNode root) {
if (root == null) {
return;
}
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()) {
root = stack.pop();
System.out.print(root.val + " ");
if (root.right != null) {
stack.push(root.right);
}
if (root.left != null) {
stack.push(root.left);
}
}
System.out.println();
}
// 非递归中序遍历
public static void inOrderNoRecursion(TreeNode root) {
if (root == null) {
return;
}
Stack<TreeNode> stack = new Stack<>();
while (!stack.isEmpty() || root != null) {
if (root != null) {
stack.push(root);
root = root.left;
} else { // 此时root = null.就打印当前栈顶元素
root = stack.pop();
System.out.print(root.val + " ");
root = root.right; // 转向右子树
}
}
System.out.println();
}
// 非递归后序遍历1
public static void postOrderNoRecursion(TreeNode root) {
if (root == null) {
return;
}
Stack<TreeNode> stack = new Stack<>();
Stack<TreeNode> helpStack = new Stack<>(); // 将遍历的结果存储在栈中,最后打印
stack.push(root);
while (!stack.isEmpty()) {
root = stack.pop();
helpStack.push(root);
if (root.left != null) {
stack.push(root.left);
}
if (root.right != null) {
stack.push(root.right);
}
}
// 打印helpStack中的数据
while (!helpStack.isEmpty()) {
root = helpStack.pop();
System.out.print(root.val + " ");
}
System.out.println();
}
// 非递归后序遍历2,省一个辅助栈的空间
public static void postOrderNoRecursion2(TreeNode root) {
if (root == null) {
return;
}
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
TreeNode pre = root; // 上一次打印的节点
while (!stack.isEmpty()) {
root = stack.peek();
if (root.left != null && root.left != pre && root.right != pre) {
stack.push(root.left);
} else if (root.right != null && root.right != pre) {
stack.push(root.right);
} else {
pre = root;
stack.pop(); // 弹出栈顶元素
System.out.print(root.val + " ");
}
}
System.out.println();
}
10、KMP
需求:给定两个字符串,s1和s2,请问在s1中是否包含子串s2?
这算是大学课程里面,数据结构书上比较难的一个算法了。主要思想还是暴力解,在暴力解的基础之上,引入了next数组的。
// s2模式串,s1是主串,在s1里面找s2
public static int indexOf(String s1, String s2) {
if (s1 == null || s2 == null || s2.length() == 0) {
return -1;
}
char[] ch1 = s1.toCharArray();
char[] ch2 = s2.toCharArray();
int[] next = getNextArray(ch2);
int index1 = 0; // 指向ch1
int index2 = 0; // 指向 ch2
while (index1 < ch1.length && index2 < ch2.length) {
if (ch1[index1] == ch2[index2]) {
index1++;
index2++;
} else if (index2 > 0) { // index2还能往前跳转的时候
index2 = next[index2]; // index2往前跳
} else { // 当前位置,既不相等,index2也不能往前跳了,说明index1位置出发行不通,index1后移
index1++;
}
}
return index2 == ch2.length ? index1 - index2 : -1;
}
private static int[] getNextArray(char[] s2) {
if (s2.length == 1) {
return new int[]{-1};
}
// 找的其实就是前后缀字符串
int[] res = new int[s2.length];
res[0] = -1;
res[1] = 0;
int i = 2; // 从第3个字符开始判断
int cn = 0;
while (i < s2.length) {
if (s2[cn] == s2[i - 1]) { // 切记这里其实是i的前一个位置
res[i++] = ++cn;
} else if (cn > 0) {
cn = res[cn];
} else {
res[i++] = 0;
}
}
return res;
}
11、Manacher
需求:在一个字符串中,问其中的最长回文子串的长度。也就是最长回文子串问题。时间复杂度O(N), 空间复杂度O(1)
暴力解,遍历每一个字符,在每一个字符的时候,往左右两边进行扩展,暴力解时间复杂度O(N^2)。
manacher也是在暴力解的基础之上,进行优化,引入了 回文半径数组。
public static int manacher(String str) {
if (str == null || str.length() == 0) {
return 0;
}
// 加工字符串,避免偶数长度的字符串遗漏一些情况
char[] chars = processStr(str);
int N = chars.length;
int R = -1; // 右边界,左闭右开区间
int C = -1; // 中心点
int max = 0;
int[] pArr = new int[N]; // 回文半径数组
for (int i = 0; i < N; i++) {
// 首先根据对称,拿到C点左侧相应的回文半径
pArr[i] = i < R? Math.min(pArr[2 * C - i], R - i) : 1;
// 根据已经计算出来的初始半径,此时再向两边扩展
while (i - pArr[i] >= 0 && i + pArr[i] < N) {
if (chars[i - pArr[i]] == chars[i + pArr[i]]) {
pArr[i]++; // 回文半径增加
} else { // 不相等,直接跳出循环
break;
}
}
// 更新R,C和max
if (i + pArr[i] > R) {
R = i + pArr[i]; // 右边界
C = i; // 以当前点作为新的中心点
}
max = Math.max(max, pArr[i]);
}
return max - 1;
}
// 每个字符之间添加#,用于间隔
private static char[] processStr(String str) {
int N = str.length();
char[] res = new char[2 * N + 1];
for (int i = 0; i < res.length; i += 2) {
res[i] = '#';
}
int index = 0;
for (int i = 1; i < res.length; i+= 2) {
res[i] = str.charAt(index++);
}
return res;
}
12、快速选择 bfprt
需求:在一个无序数组中,返回 第 K 小的数字。时间复杂度O(N),空间复杂度O(1)。
// 0、排序之后,再找第k小的数,时间复杂度O(N*logN),这样写,面试直接挂。
// 1、常规解法,就是TopK问题,使用一个大根堆,将所有数过一遍大根堆就行,这里就不追溯了。时间O(N * logK),空间O(K)
// 2、归并排序中的merge函数,(荷兰国旗问题优化)。
// 因为这里的pivot是随机选取的,在数学证明上,时间复杂度是收敛于O(N)的
public static int fatsSelect(int[] nums, int k) {
fastSelect(nums, 0, nums.length - 1, k - 1);
return nums[k - 1];
}
private static void fastSelect(int[] nums, int l, int r, int k) {
if (l >= r) {
return;
}
int index = l + (int) (Math.random() * (r - l)) + 1; // 随机值
int pivot = nums[index];
int[] mid = partition(nums, pivot);
if (mid[0] <= k && k <= mid[1]) {
return;
} else if (k < mid[0]) { // 往左侧走
fastSelect(nums, l, mid[0] - 1, k);
} else { // 往右侧走
fastSelect(nums, mid[1] + 1, r, k);
}
}
// 荷兰国旗问题优化
private static int[] partition(int[] nums, int l, int r, int pivot) {
int less = l - 1; // 小于区
int more = r + 1; // 大于区
int index = l;
while (less < more) {
if (nums[index] == pivot) {
index++;
} else if (nums[index] < pivot) {
swap(nums, index++, ++less); // 两数交换
} else {
swap(nums, index, --more);
}
}
return new int[]{less + 1, more - 1};
}
// 2、bfprt算法,时间复杂度严格控制在O(N)
// 严格解析,请看https://blog.csdn.net/x0919/article/details/122246065
public static int bfprt(int[] arr, int l, int r, int k) {
if (l == r) {
return arr[l];
}
int pivot = medianOfMedians(arr, l, r);
// 根据基准值进行荷兰国旗问题优化
int[] mid = netherlands(arr, l, r, pivot);
if (mid[0] <= k && k <= mid[1]) {
return arr[k];
} else if (mid[0] > k) {
return bfprt(arr, l, mid[0] - 1, k);
} else {
return bfprt(arr, mid[1] + 1, r, k);
}
}
private static int[] netherlands(int[] arr, int l, int r, int pivot) {
int less = l - 1;
int more = r + 1;
int index = l;
while (index < more) {
if (arr[index] < pivot) {
swap(arr, index++, ++less);
} else if (arr[index] > pivot) {
swap(arr, index, --more);
} else {
index++;
}
}
return new int[]{less + 1, more - 1};
}
private static void swap(int[] arr, int l, int r) {
int tmp = arr[l];
arr[l] = arr[r];
arr[r] = tmp;
}
// 获取基准值
private static int medianOfMedians(int[] arr, int l, int r) {
// 5个数 5个数一组,取5个数的中间值
int len = r - l + 1;
int size = len / 5;
int offset = len % 5 == 0 ? 0 : 1;
int[] tmp = new int[size + offset];
for (int i = 0; i < tmp.length; i++) {
int left = l + 5 * i; // 5个数的左边界
int right = Math.min(r, l + 4); // 5个数的右边界
tmp[i] = sortAndGetMidNum(arr, left, right);
}
// 再返回tmp数组中的中间值
return bfprt(tmp, 0, tmp.length - 1, tmp.length / 2);
}
// 排序这5个数,并返回中间值
private static int sortAndGetMidNum(int[] arr, int left, int right) {
// 直接插入排序
for (int i = left; i < right; i++) {
int cur = arr[i];
int j = i - 1;
for (; j >= left; j--) {
if (arr[j] > arr[j + 1]) {
arr[j + 1] = arr[j];
} else {
break;
}
}
arr[j + 1] = cur;
}
return arr[left + (right - left) / 2]; // 返回中间值
}
13、滑动窗口
需求:常常用于子数组求解之类问题。
维持L、R边界,一般来说都是左闭右开区间的。
/**
* Created by Terry
* User: Administrator
* Date: 2022-06-26
* Time: 15:40
* Description: 窗口最大值。
* 假设一个固定大小为W的窗口,依次划过arr,
* 返回每一次滑出状况的最大值
* 例如,arr = [4,3,5,4,3,3,6,7], W = 3
* 返回:[5,5,5,4,6,7]
*/
public class Code01_WindowMaxNumber {
public static void main(String[] args) {
int[] arr = {4, 3, 5, 4, 3, 3, 6, 7};
int w = 3;
System.out.println(Arrays.toString(windowMaxNumber(arr, w)));
}
public static int[] windowMaxNumber(int[] arr, int w) {
if (arr == null || arr.length == 0 || arr.length < w) {
return new int[]{};
}
int N = arr.length;
int[] ans = new int[N - w + 1];
int index = 0;
LinkedList<Integer> queue = new LinkedList<>(); // 双端队列
for (int i = 0; i < arr.length; i++) {
while (!queue.isEmpty() && arr[queue.peekLast()] <= arr[i]) { // 维持头部大,尾部小的结构
queue.pollLast();
}
queue.addLast(i);
if (i - queue.peekFirst() == w) {
queue.pollFirst();
}
if (i >= w - 1) {
ans[index++] = arr[queue.peekFirst()];
}
}
return ans;
}
}
14、加强堆
需求:系统提供的堆,在压入元素进去之后,若此时需要修改堆中某个元素的数据,然后修改之后,堆的结构应该发生改变,系统提供的堆不能实现这个事。需要自己改堆结构。
举个例子:现在有一个大根堆 heap,类型为Node节点,比较方式是 Node里的val值。
假设现在修改堆中某一个节点node的val值,修改之后,需要手动调用 函数(向堆顶走、向堆下面走)两种情况,才能维持堆的结构。
// 手改堆。核心点就在 反向索引表indexMap,能够获取对象在数组中的下标值
public class HeapGenerate<T> {
private ArrayList<T> arr; // 存储节点的数组
private HashMap<T, Integer> indexOfMap; // 存储每个节点在堆上的下标
private int size; // 堆的大小
private Comparator<? super T> comp; // 比较器
public HeapGenerate(Comparator<? super T> comp) {
this.arr = new ArrayList<>();
this.indexOfMap = new HashMap<>();
this.size = 0;
this.comp = comp;
}
public boolean isEmpty() {
return this.size == 0;
}
public int size() {
return size;
}
public List<T> getAllElements() {
List<T> list = new ArrayList<>();
for (T v : arr) {
list.add(v);
}
return list;
}
public boolean contains(T obj) {
return indexOfMap.containsKey(obj); // 查看当前堆中是否有该对象
}
public T peek() {
return arr.get(0);
}
public void add(T value) {
this.arr.add(value);
this.indexOfMap.put(value, size); // 存储下标值
heapInsert(size++); // 往上调整
}
// 弹出堆顶结果
public T poll() {
T res = arr.get(0);
swap(0, size - 1); // 第一个数据和最后一个数据进行交换
indexOfMap.remove(res); // 删除res对应的下标
arr.remove(--size); // 删除在数组上的数据
heapify(0); // 向下调整
return res;
}
// 手改堆的核心,能删除非堆顶元素
public void remove(T obj) {
T replace = arr.get(size - 1); // 拿到最后一个元素
int index = indexOfMap.get(obj);
indexOfMap.remove(obj); // 删除在表中的下标
arr.remove(--size); // 删除数组中的最后一个元素
if (replace != obj) { // 被删除的元素并不是数组中的最后一个元素
arr.set(index, replace);
indexOfMap.put(replace, index); // 新的下标
resign(replace);
}
}
// 手改堆的核心方法
public void resign(T value) { // 根据对象,获取对象在数组中的下下标,从而进行调整
heapInsert(indexOfMap.get(value));
heapify(indexOfMap.get(value)); // 二者,只可能有一个会调用,只可能向上或向下
}
private void heapify(int i) {
int left = (i << 1) + 1;
while (left < size) {
int maxChild = left + 1 < size && comp.compare(arr.get(left + 1), arr.get(left)) < 0?
left + 1 : left;
maxChild = comp.compare(arr.get(maxChild), arr.get(i)) < 0? maxChild : i; // 跟父节点做判断
if (maxChild == i) {
break;
}
swap(i, maxChild);
i = maxChild;
left = (i << 1) + 1; // 再次刷新左孩子
}
}
// 往上走,调整堆结构
private void heapInsert(int i) {
// 根据自定义的比较器进行比较
// 此处除以2,用位运算代替,要判断i是大于0才行
while (i > 0 && comp.compare(arr.get(i), arr.get((i - 1) >> 1)) < 0) {
swap(i, (i - 1) >> 1);
i = (i - 1) >> 1;
}
}
// 不仅要更新在数组上的值,还要更新indexOfMap中的值
private void swap(int up, int down) {
T o1 = arr.get(up);
T o2 = arr.get(down);
indexOfMap.put(o1, down);
indexOfMap.put(o2, up);
arr.set(up, o2); // 更新
arr.set(down, o1); // 更新
}
}
15、有序表
也就是能够排序的一些结构,比如AVL树、SB树、跳表、红黑树等。比较好写的可能就是SB树。
// Size Balance Tree,通过节点的数量来调整平衡的
private static class SBTNode<K extends Comparable<K>, V> {
public K key;
public V value;
public int size;
public SBTNode<K, V> left;
public SBTNode<K, V> right;
public SBTNode(K key, V value) {
this.key = key;
this.value = value;
size = 1;
}
}
private static class SizeBalanceTree<K extends Comparable<K>, V> {
private SBTNode<K, V> root;
private SBTNode<K, V> getIndex( SBTNode<K, V> cur, int kth) {
if (kth == (cur.left != null ? cur.left.size : 0) + 1) {
return cur;
} else if (kth <= (cur.left != null ? cur.left.size : 0)) {
return getIndex(cur.left, kth);
} else {
return getIndex(cur.right, kth - (cur.left != null ? cur.left.size : 0) - 1);
}
}
public K getIndexKey(int index) {
if (index < 0 || index >= this.size()) {
throw new RuntimeException("invalid parameter.");
}
return getIndex(root, index + 1).key;
}
public V getIndexValue(int index) {
if (index < 0 || index >= this.size()) {
throw new RuntimeException("invalid parameter.");
}
return getIndex(root, index + 1).value;
}
public int size() {
return root == null ? 0 : root.size;
}
public void put(K key, V val) {
if (key == null) {
throw new RuntimeException("key is invalid.");
}
SBTNode<K, V> lastNode = findLastIndex(key);
if (lastNode != null && key.compareTo(lastNode.key) == 0) { // 更新值的情况
lastNode.value = val;
} else { // 新插入值
root = add(root, key, val);
}
}
// 返回等于key的,或者key的父节点。
private SBTNode<K, V> findLastIndex(K key) {
SBTNode<K, V> pre = root;
SBTNode<K, V> cur = root;
while (cur != null) {
pre = cur;
if (key.compareTo(cur.key) == 0) {
break;
} else if (key.compareTo(cur.key) < 0) {
cur = cur.left;
} else {
cur = cur.right;
}
}
return pre;
}
private SBTNode<K, V> add(SBTNode<K, V> node, K key, V val) {
if (node == null) {
return new SBTNode<K, V>(key, val);
} else {
node.size++;
if (key.compareTo(node.key) < 0) {
node.left = add(node.left, key, val);
} else {
node.right = add(node.right, key, val);
}
// 维持平衡
return maintain(node);
}
}
public void remove(K key) {
if (key == null) {
throw new RuntimeException("key is invalid.");
}
if (containsKey(key)) {
root = delete(root, key);
}
}
private SBTNode<K, V> delete(SBTNode<K, V> node, K key) {
node.size--;
int compare = key.compareTo(node.key);
if (compare < 0) {
node.left = delete(node.left, key);
} else if (compare > 0) {
node.right = delete(node.right, key);
} else { // ==0的情况
if (node.right == null) { // 有左孩子的情况,或者左右孩子都没有
node = node.left;
} else if (node.left == null) { // 有右孩子的情况
node = node.right;
} else { // 左右孩子都有的情况
SBTNode<K, V> pre = null;
SBTNode<K, V> cur = node.right;
cur.size--;
while (cur.left != null) {
pre = cur;
cur = cur.left;
cur.size--;
}
if (pre != null) {
pre.left = cur.right;
cur.right = node.right;
}
cur.left = node.left;
cur.size = cur.left.size + (cur.right != null ? cur.right.size : 0) + 1;
node = cur;
}
}
// 维持平衡---可以不用维持平衡,在add的时候再维护
// node = maintain(node);
return node;
}
public boolean containsKey(K key) {
if (key == null) {
throw new RuntimeException("key is invalid.");
}
SBTNode<K, V> lastNode = findLastIndex(key);
return lastNode != null && key.compareTo(lastNode.key) == 0;
}
private SBTNode<K, V> maintain(SBTNode<K, V> node) {
if (node == null) {
return null;
}
// 计算node的下一级节点数和 下下一级节点数
int leftSize = node.left != null ? node.left.size : 0;
int rightSize = node.right != null ? node.right.size : 0;
int leftLeftSize = node.left != null && node.left.left != null ? node.left.left.size : 0; // LL
int leftRightSize = node.left != null && node.left.right != null ? node.left.right.size : 0; // LR
int rightLeftSize = node.right != null && node.right.left != null ? node.right.left.size : 0; // RL
int rightRightSize = node.right != null && node.right.right != null ? node.right.right.size : 0; // RR
if (leftLeftSize > rightSize) { // RR型旋转
node = rightRotate(node);
node.right = maintain(node.right); // 先调整node下级节点的平衡
node = maintain(node);
} else if (leftRightSize > rightSize) { // LR型旋转
node.left = leftRotate(node.left); // 先左旋转
node = rightRotate(node); // 再右旋转
node.left = maintain(node.left);
node.right = maintain(node.right); // 先维持node的下级节点
node = maintain(node);
} else if (rightLeftSize > leftSize) { // RL型旋转
node.right = rightRotate(node.right);
node = leftRotate(node);
node.left = maintain(node.left);
node.right = maintain(node.right);
node = maintain(node);
} else if (rightRightSize > leftSize) { // LL型旋转
node = leftRotate(node);
node.left = maintain(node.left);
node = maintain(node);
}
return node;
}
private SBTNode<K, V> leftRotate(SBTNode<K, V> node) {
SBTNode<K, V> newHead = node.right;
node.right = newHead.left;
newHead.left = node;
newHead.size = node.size;
node.size = (node.left != null ? node.left.size : 0) + (node.right != null ? node.right.size : 0) + 1;
return newHead;
}
private SBTNode<K, V> rightRotate(SBTNode<K, V> node) {
SBTNode<K, V> newHead = node.left;
node.left = newHead.right;
newHead.right = node;
newHead.size = node.size;
node.size = (node.left != null ? node.left.size : 0) + (node.right != null ? node.right.size : 0) + 1;
return newHead;
}
public V get(K key) {
if (key == null) {
throw new RuntimeException("key is invalid.");
}
SBTNode<K, V> lastNode = findLastIndex(key);
if (lastNode != null && key.compareTo(lastNode.key) == 0) {
return lastNode.value;
}
return null;
}
public K firstKey() {
if (root == null) {
return null;
}
SBTNode<K, V> node = root;
while (node.left != null) {
node = node.left;
}
return node.key;
}
public K lastKey() {
if (root == null) {
return null;
}
SBTNode<K, V> node = root;
while (node.right != null) {
node = node.right;
}
return node.key;
}
// <= key的,最接近key的
public K floorKey(K key) {
if (key == null) {
throw new RuntimeException("key is invalid.");
}
SBTNode<K, V> ans = null;
SBTNode<K, V> cur = root;
while (cur != null) {
if (key.compareTo(cur.key) == 0) {
ans = cur;
break;
} else if (key.compareTo(cur.key) < 0) { // key < cur.key
cur = cur.left;
} else { // key >= cur.key
ans = cur;
cur = cur.right;
}
}
return ans == null ? null : ans.key;
}
// >= key的,最接近key的
public K ceilingKey(K key) {
if (key == null) {
throw new RuntimeException("key is invalid.");
}
SBTNode<K, V> ans = null;
SBTNode<K, V> cur = root;
while (cur != null) {
if (key.compareTo(cur.key) == 0) {
ans = cur;
break;
} else if (key.compareTo(cur.key) < 0) { // key < cur.key
ans = cur;
cur = cur.left;
} else { // key >= cur.key
cur = cur.right;
}
}
return ans == null? null : ans.key;
}
}
16、单调栈
需求:在一个无序数组中,找一个元素的左右两侧第一个比它大(小)的数。时间复杂度O(N),空间复杂度O(N)。
细分为单调递增栈、单调递减栈。LeetCode练习题。
- 单调递增栈:从栈顶往下,元素越来越大。用于找元素的两侧第一个比它大的数。
- 单调递减栈:从栈顶往下,元素越来越小。用于找元素的两侧第一个比它小的数。
// 单调递减栈。 反之单调递增栈,只需修改第6行while循环中的 <=符号即可
public static void monotonousStack(int[] nums) {
Stack<Integer> stack = new Stack<>(); // 存入的数组的下标值
for (int i = 0; i < nums.length; i++) {
// 下方的具体是 < 还是<=,也是看题意来定的
while (!stack.isEmpty() && nums[i] <= nums[stack.peek()]) {
// 此时弹出的pos下标,有以下性质:(假设弹出栈顶元素pos后,此时栈顶元素 = k)
// 1、[i]的元素 <= [pos]
// 2、[k] < [pos]的元素
// 所有就有 [k] < [pos] && pos >= [i],
// 所有对于pos来说,左右两侧的比它小的数就出来了
int pos = stack.pop();
int k = stack.isEmpty() ? -1 : stack.peek();
// 后续操作根据题意来定
}
stack.push(i);
}
}
} else { // key >= cur.key
ans = cur;
cur = cur.right;
}
}
return ans == null ? null : ans.key;
}
// >= key的,最接近key的
public K ceilingKey(K key) {
if (key == null) {
throw new RuntimeException("key is invalid.");
}
SBTNode ans = null;
SBTNode cur = root;
while (cur != null) {
if (key.compareTo(cur.key) == 0) {
ans = cur;
break;
} else if (key.compareTo(cur.key) < 0) { // key < cur.key
ans = cur;
cur = cur.left;
} else { // key >= cur.key
cur = cur.right;
}
}
return ans == null? null : ans.key;
}
}
### 15、单调栈
**需求:**在一个无序数组中,找一个元素的左右两侧第一个比它大(小)的数。时间复杂度O(N),空间复杂度O(N)。
细分为单调递增栈、单调递减栈。[LeetCode练习题](https://leetcode.cn/problems/trapping-rain-water/description/)。
- 单调递增栈:从栈顶往下,元素越来越大。用于找元素的两侧第一个比它大的数。
- 单调递减栈:从栈顶往下,元素越来越小。用于找元素的两侧第一个比它小的数。
~~~java
// 单调递减栈。 反之单调递增栈,只需修改第6行while循环中的 <=符号即可
public static void monotonousStack(int[] nums) {
Stack stack = new Stack<>(); // 存入的数组的下标值
for (int i = 0; i < nums.length; i++) {
// 下方的具体是 < 还是<=,也是看题意来定的
while (!stack.isEmpty() && nums[i] <= nums[stack.peek()]) {
// 此时弹出的pos下标,有以下性质:(假设弹出栈顶元素pos后,此时栈顶元素 = k)
// 1、[i]的元素 <= [pos]
// 2、[k] < [pos]的元素
// 所有就有 [k] < [pos] && pos >= [i],
// 所有对于pos来说,左右两侧的比它小的数就出来了
int pos = stack.pop();
int k = stack.isEmpty() ? -1 : stack.peek();
// 后续操作根据题意来定
}
stack.push(i);
}
}
17、数位DP
最简单的数位DP,请看 leetcode233题 数字1的个数。
思路:把n这个数字,转换成字符串类型,然后从左往右开始枚举每一个位置的数值,类似于全排列的那种递归展开。
from functools import cache
# leetcode 1012题 至少有1位重复数字
class Solution:
def numDupDigitsAtMostN(self, n: int) -> int:
# 现在的问题是,如何将cnt数组,进行状态转移
# 换个思路:题目要计算有重复字符的数字,那么【全部数字组合】-【不重复数字组合】
# 剩下的就是 【有重复字符的组合数】
s = str(n)
@cache
# i指向字符串,
# status的二进制位信息,表示每个位置的数字是否出现过 (左神讲的 状态压缩)
# is_limit 表示是否到达n的上限了
# pre_num 表示 0~i-1位置,是否生成了数值
def f(i: int, status: int, is_limit: bool, pre_num: bool) -> int:
if i == len(s):
return int(pre_num)
ans = 0
if not pre_num:
ans = f(i + 1, status, False, False)
# 枚举
# 0~i-1位置还没有生成数值的话,这个位置开始生成,比如从1开始,避开前导0
low = 0 if pre_num else 1
up = int(s[i]) if is_limit else 9
for d in range(low, up + 1):
if (status >> d) & 1 == 0: # 说明d这个数字还没出现过
status += (1 << d) # 将第 d位的二进制位 标记
ans += f(i + 1, status, is_limit and d == up, True)
status -= (1 << d) # 恢复现场
return ans
return n - f(0, 0, True, False)
# 正向思考,枚举每一个位置
def numDupDigitsAtMostN1(self, n: int) -> int:
s = str(n)
cnt = [0] * 10
def f(i: int, is_limit: bool, pre_num: bool) -> int:
if i == len(s):
for x in cnt:
if x >= 2: return True
return False
ans = 0
if not pre_num:
ans = f(i + 1, False, False)
# 枚举
# 0~i-1位置还没有生成数值的话,这个位置开始生成,比如从1开始,避开前导0
low = 0 if pre_num else 1
up = int(s[i]) if is_limit else 9
for d in range(low, up + 1):
cnt[d] += 1
ans += f(i + 1, is_limit and d == up, True)
cnt[d] -= 1
return ans
return f(0, True, False)
18、快速幂
核心思想:将指数折半拆分进行计算,例如指数8 等价于 4 + 4,那么只需要计算 a^4之后,再对其平方,就能得到a ^8。
// 快速幂, a^b次方
// 公式:(n1 * n2) % MOD = [(n1 % MOD) * (n2 % MOD)] % MOD
private int MOD = 1337;
private long quickMul(int a, int b) {
if (b == 0) return 1;
if (b == 1) return a;
long sum = quickMul(a, b / 2) % MOD;
// b是奇数,就拆分为偶数+偶数+1
// b是偶数,就拆分为 偶数+偶数
return b % 2 == 0? sum * sum % MOD : sum * sum * a % MOD;
}