编程题分类——链表
目录
- 前言
- 经验
- 正文
-
- 1. [两数相加](https://leetcode-cn.com/problems/add-two-numbers/)
- 2. [判断链表中是否有环 ----- 有关单链表中环的问题](https://www.cnblogs.com/yorkyang/p/10876604.html)
-
- 2.1 判断单链表中是否有环
- 2.2 判断单链表的入口点的地址
- 2.3 如果存在环,求出环上各点的个数。
- 3.[旋转链表](https://leetcode-cn.com/problems/rotate-list/)
- 4. [链表中将所有的偶数移到奇数后面不改变原来的相对位置?](https://blog.csdn.net/u013309870/article/details/62897748)
- 5. [判断回文链表](https://leetcode-cn.com/problems/palindrome-linked-list/submissions/)
- 6. [删除链表中重复的结点](https://www.nowcoder.com/practice/fc533c45b73a41b0b44ccba763f866ef?tpId=13&tqId=23450&ru=/ta/coding-interviews&qru=/ta/coding-interviews/question-ranking)
- 7. [删除链表的倒数第 N 个结点](https://leetcode-cn.com/problems/remove-nth-node-from-end-of-list/)
- 8. 单向链表中如何高效删除一个结点(只给定头指针和指向当前结点的指针)
- 9. [反转链表](https://www.nowcoder.com/practice/75e878df47f24fdc9dc3e400ec6058ca?tpId=117)
- 10. 合并K个升序链表
- 11. 二叉树的直径
- 12. 二叉树中的最大路径和
- 13. 最长同值路径
- 参考
前言
经验
正文
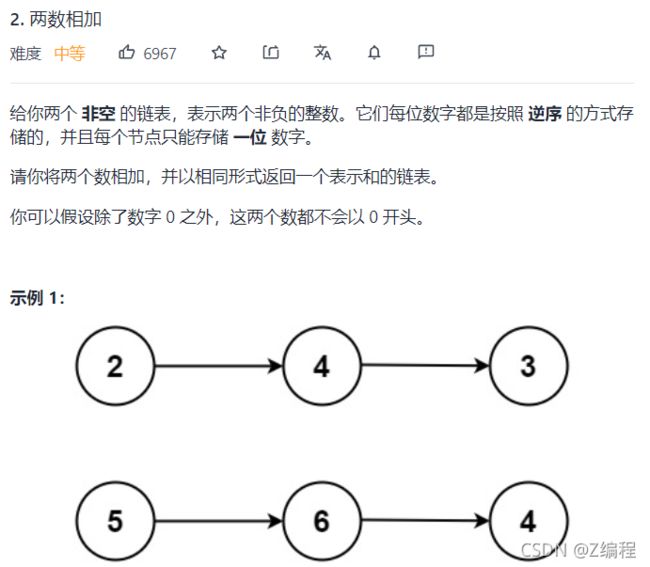
1. 两数相加
code
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* addTwoNumbers(ListNode* head1, ListNode* head2) {
//这题的条件是属于相对苛刻的,两个节点相加的值居然可以加到后面的那个节点上去。
//这题是借助于大数相加的原理
if(head1==nullptr||head2==nullptr)
return nullptr;
ListNode* node1 = head1;
ListNode* node2 = head2;
int len1 = 1;
int len2 = 1;
while(node1->next!=NULL)//这里错第二次了,老是写成node!=NULL
{
++len1;
node1 = node1->next;
}
while(node2->next!=NULL)
{
++len2;
node2 = node2->next;
}
ListNode *head = new ListNode(-1);//创建一个虚拟节点
ListNode *node = head;
while(node1&&len1<len2)
{
++len1;
node1->next = new ListNode(0);
node1 = node1->next;
}
while(node2&&len1>len2)
{
++len2;
node2->next = new ListNode(0);
node2 = node2->next;
}
node1 = head1;
node2 = head2;
bool flag = false;
int sum=0;
while(node1&&node2)
{
sum = flag+node1->val+node2->val;
flag = sum>=10?true:false;
node->next = new ListNode(sum%10);
node = node->next;
node1 = node1->next;
node2 = node2->next;
}
if(flag&&node)
{
node->next = new ListNode(flag);
node = node->next;
}
return head->next;
}
};
2. 判断链表中是否有环 ----- 有关单链表中环的问题
其实最重要的就是要明白的一个关系:
就是头节点到入口点的距离 = 相遇点到入口点的距离。
求相遇点就用双指针就可以了。
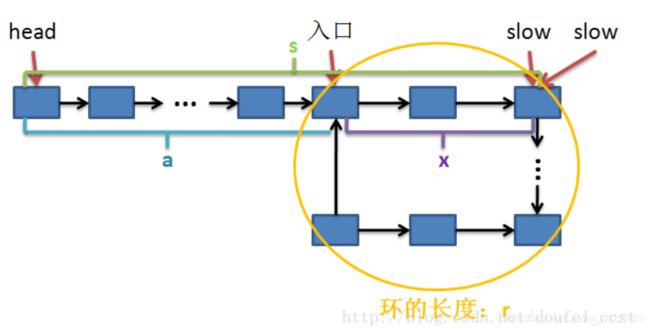
2.1 判断单链表中是否有环
快慢指针,若两个指针相遇,则证明有环。
code
//如何判断是否有环
typedef struct node{
char data;
node *next;
};
bool exitLoop(Node *head)
{
Node *fast,*slow;
slow = fast = head;
while(slow!=NULL&&fast->next!=NUL)//这样就可以判断有没有环了,如果没环,第二个节点肯定很早就到达末尾了,不会有slow = fast的这种情况。
{
slow = slow->next;
fast = fast->next->next;
if(slow==fast)
return true;
}
return false;
}
2.2 判断单链表的入口点的地址
相遇点到入口点的距离=头节点到入口点的距离
code
/*
struct ListNode {
int val;
struct ListNode *next;
ListNode(int x) :
val(x), next(NULL) {
}
};
*/
class Solution {
public:
ListNode* EntryNodeOfLoop(ListNode* head) {
//这题第一眼看到也是没有多少想法,https://www.cnblogs.com/yorkyang/p/10876604.html
ListNode *fast,*slow;
slow = fast = head;
while(slow!=NULL&&fast->next!=NULL)
{
slow = slow->next;
fast = fast->next->next;
if(slow==fast)//这时找到入口点就停下来
break;
}
if(slow==NULL||fast->next==NULL)//你这里肯定判断有没有环了,若有环才继续下一步
return NULL;
ListNode *ptr1 = head;
ListNode *ptr2 = slow;
while(ptr1!=ptr2)//有一个相等关系:头->入口点 = 两个指针的相遇点->入口点/。这两段距离是相等的
{
ptr1 = ptr1->next;
ptr2 = ptr2->next;
}
return ptr1;
}
};
2.3 如果存在环,求出环上各点的个数。
思路1:记录下相遇节点存入临时变量tempPtr,然后让slow(或者fast,都一样)继续向前走slow = slow -> next;一直到slow == tempPtr; 此时经过的步数就是环上节点的个数;
思路2: 从相遇点开始slow和fast继续按照原来的方式向前走slow = slow -> next; fast = fast -> next -> next;直到二者再次项目,此时经过的步数就是环上节点的个数 。
3.旋转链表
题目
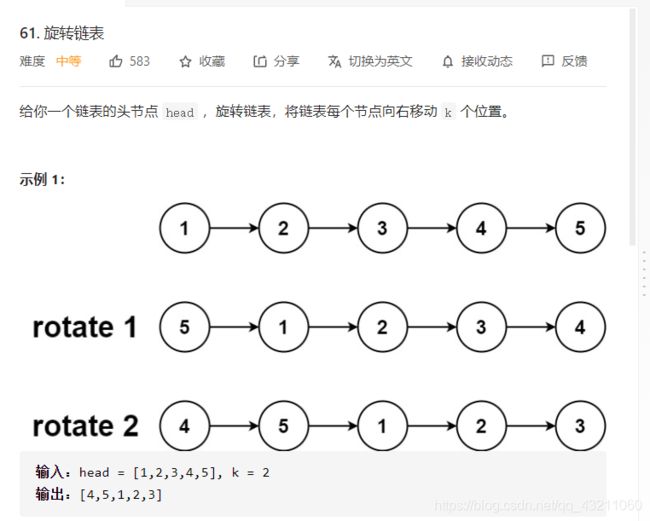
思路:先收尾相连,然后在最后面的那个指针向前移动k个位置,移到那个位置后,断开当前链表。**注意一点点是若k的大小大于这个链表的长度的话,则哟啊进行取余的操作。
code
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* rotateRight(ListNode* head, int k) {
if(k==0||head==nullptr||head->next==nullptr)
return head;
int n = 1;
ListNode* node = head;
while(node->next!=nullptr)//通过这个可以计算出当前有多少元素
{
node = node->next;
n++;
}
int add = n-k%n;
if(add==n)//若需要右移的元素刚好是n的整数倍
return head;
node->next = head;//收尾相连
while(add--)//根据这个,移到要断开的那个位置
{
node = node->next;
}
ListNode *ret = node->next;//断开的方式就是就是把下一个节点赋给一个临时变量。然后,将其指向nullptr。
node->next = nullptr;
return ret;
}
};
题解
这题有几个点:
- 首先,将链表首尾相连
- 得出链表有多少个元素。
- 注意移动的元素的数量有可能大于n.所以要取余。
- 注意,这里的这个add,移动的个数是n-k。
4. 链表中将所有的偶数移到奇数后面不改变原来的相对位置?
code
ListNode* oddEvenList(ListNode* head)
{
if (head == nullptr || head->next == nullptr)
return head;
ListNode* q = NULL;
ListNode* p = head;
while (p)
{
if (p->val & 1)
{
if (q == NULL)
{
swap(head->val, p->val);
q = head;
}
else
{
q = q->next;//相当于q所指的位置,就是所有奇数的最后一位
swap(q->val, p->val);
}
}
p = p->next;
}
return head;
}
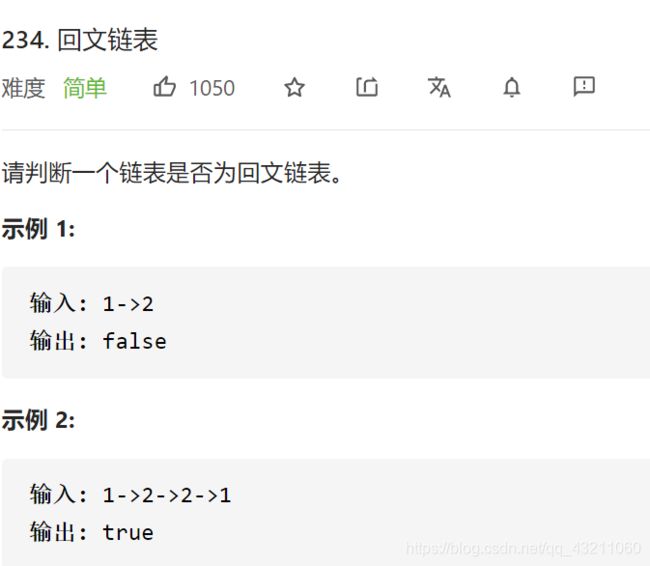
5. 判断回文链表
class Solution {
public:
bool isPalindrome(ListNode* head)
{
if (head == nullptr)
{
return true;
}
// 找到前半部分链表的尾节点并反转后半部分链表
ListNode* firstHalfEnd = endOfFirstHalf(head);//先使用快慢指针找到中间节点
ListNode* secondHalfStart = reverseList(firstHalfEnd->next);//将该节点后面的所有节点进行翻转,注意传入的节点为Next节点
// 判断是否回文
ListNode* p1 = head;
ListNode* p2 = secondHalfStart;
bool result = true;
while (result && p2 != nullptr)
{
if (p1->val != p2->val)
{
result = false;
}
p1 = p1->next;
p2 = p2->next;
}
// 还原链表并返回结果
firstHalfEnd->next = reverseList(secondHalfStart);
return result;
}
ListNode* reverseList(ListNode* head)
{
ListNode* prev = nullptr;
ListNode* curr = head;
while (curr != nullptr)
{
ListNode* nextTemp = curr->next;//先储存下这个next节点
curr->next = prev;//将指针进行反转
prev = curr;//把cur变成pre,把next变成cur
curr = nextTemp;
}
return prev;//error1:注意返回的pre,这个才是最后的根节点
}
ListNode* endOfFirstHalf(ListNode* head)
{//返回的是链表中间节点的指针
ListNode* fast = head;
ListNode* slow = head;
while (fast->next != nullptr && fast->next->next != nullptr)
{
fast = fast->next->next;
slow = slow->next;
}
return slow;
}
};
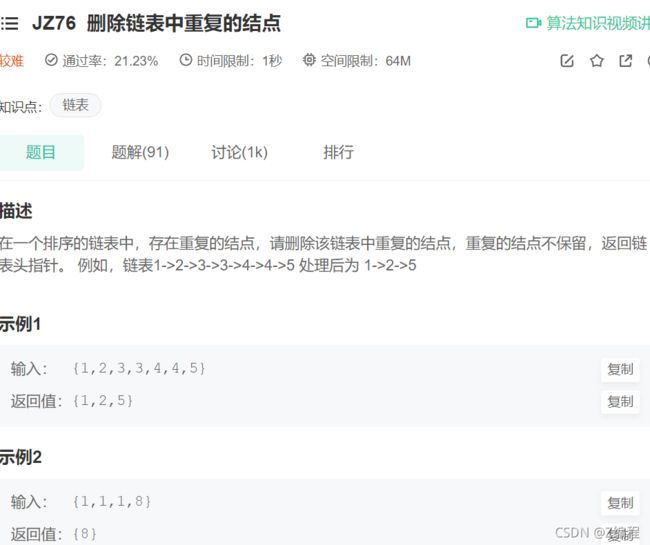
6. 删除链表中重复的结点
方法一:递归的方法。 就是比如头节点的几个是相同的,然后的时候,就换一个节点跟前面的节点的值不一样的作为头结点进行返回。
code
/*
struct ListNode {
int val;
struct ListNode *next;
ListNode(int x) :
val(x), next(NULL) {
}
};
*/
class Solution {
public:
ListNode* deleteDuplication(ListNode* head) {
//采用递归的方式进行处理
if(head==nullptr||head->next==nullptr)//error1:忘记只有一个节点也要返回
return head;
if(head->val==head->next->val)//递归的处理方式
{
ListNode *p = head->next->next;
while(p!=NULL&&p->val==head->next->val)
{
p = p->next;
}
head = p;
return deleteDuplication(head);
}
head->next = deleteDuplication(head->next);
return head;
}
};
总结:
- 作为空节点与单个节点的返回。
- 如果第一个节点和第二个节点相同,就继续比较第三个节点和第2个节点的值。用个p往后面移。等到没有和前面的节点相同的情况下,作为head往下面传。
- 特殊情况处理完后,就类似于链表的连接,把head->next不断的往下传。
方法二:非递归法,从前往后走。注意,while循环里,一般先进行正常情况的判断,然后再else。并且,注意让你删除链表中的某些元素。一定要delete这个元素。最好再置个空。然后就是指针的前面一定要进行判断。
code
/*
struct ListNode {
int val;
struct ListNode *next;
ListNode(int x) :
val(x), next(NULL) {
}
};
*/
class Solution {
public:
ListNode* deleteDuplication(ListNode* head) {
//非递归版,从前往后走。跳过一些元素就好了
if(head==nullptr||head->next==nullptr)
return head;
ListNode* pre = nullptr;
ListNode* node = head;
ListNode *next = node->next;
while(next)
{
if(node->val!=next->val)//error1:未先进行正常情况的判断
{
pre = node;
node = next;
next = next->next;
}
else
{
while(node->val==next->val)
{
next = next->next;
}
while(node!=next)
{
ListNode* cur = node->next;
delete node;
node = cur;
}
if(pre==nullptr)
head = node;
else
{
pre->next = node;
}
if(next)//2. error2:忘记判断,就直接想next
next = next->next;
}
}
return head;
}
};
7. 删除链表的倒数第 N 个结点
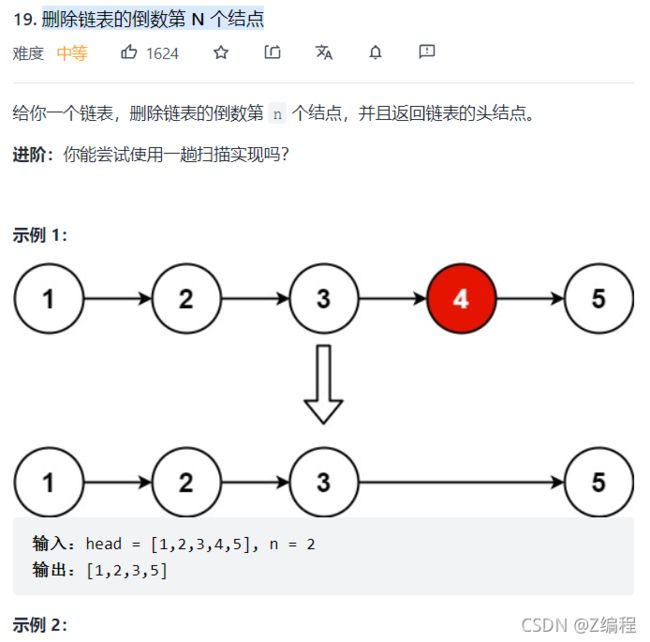
要点:1. 尽量弄个虚拟节点,这样会好弄很多。2. 最后最好删掉那个虚拟节点。
code
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
//基本就是新头节点+前后指针+删除慢指针的下一个节点
if(head==nullptr||n==0)
return head;
ListNode* newhead = new ListNode(0);
newhead->next = head;
ListNode *slow = newhead;
ListNode *fast = newhead;
while(n)//3 2 1
{
fast = fast->next;
n--;
}
while(fast->next)
{
fast = fast->next;
slow = slow->next;
}
ListNode *delNode = slow->next;
slow->next = delNode->next;
delete delNode;
delNode = nullptr;
ListNode *res = newhead->next;
return res;
}
};
8. 单向链表中如何高效删除一个结点(只给定头指针和指向当前结点的指针)
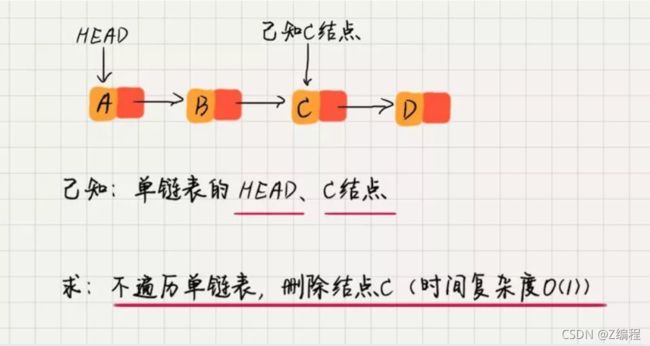
思路:如果按照正常的方法去遍历删除,时间复杂度肯定是O(N)。
- 所以,平常的那种方法是不行的,所以,我们换种思路:我们是不是一定要删除这个节点,其实是不是的。我们要删除的是这个节点的数据。所以,我们可以把这个节点的数据和下一个节点的数据进行交换。然后删除下一个节点,从而我们这样的时间复杂度就是O(1)了。
- 但同时,你也要想到,若要删除的节点是最后一个节点,则遍历到最后一个节点,这个是避免不了的。这种方法的时间复杂度会是O(N). 但时间复杂度在这边的计算是,在n-1的情况是O(1),只有在一种情况下是O(N). 所以(n-1O(1) +1O(N))/n = O(1)
参考1
参考2
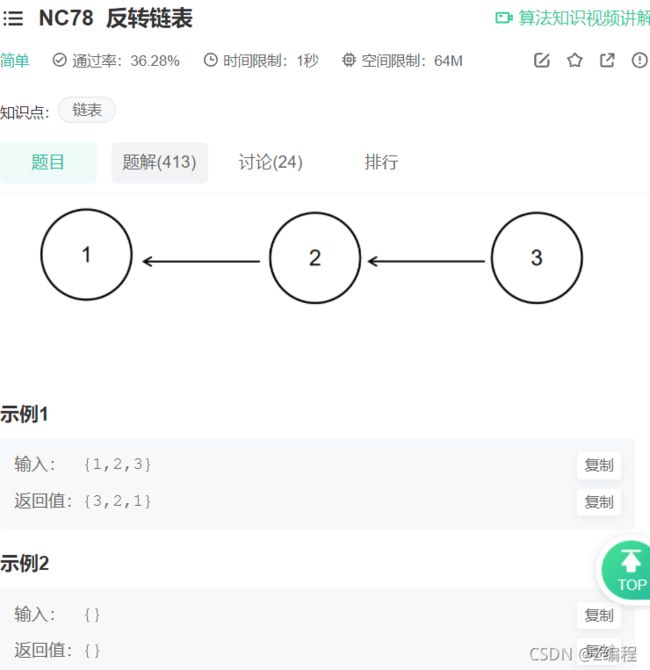
9. 反转链表
/*
struct ListNode {
int val;
struct ListNode *next;
ListNode(int x) :
val(x), next(NULL) {
}
};*/
class Solution {
public:
ListNode* ReverseList(ListNode* head) {
if(head==NULL||head->next==NULL)
return head;
ListNode* ans = ReverseList(head->next);
head->next->next = head;
head->next = NULL;
return ans;
}
};
2. 迭代
code
/*
struct ListNode {
int val;
struct ListNode *next;
ListNode(int x) :
val(x), next(NULL) {
}
};*/
class Solution {
public:
ListNode* ReverseList(ListNode* head) {
if(head==nullptr)
return nullptr;
ListNode* pre = NULL;
ListNode* node = head;
ListNode* next = NULL;
ListNode* reverseHead = NULL;
while(node)
{
next = node->next;
if(next==NULL)
reverseHead = node;
node->next = pre;
pre = node;
node = next;
}
return reverseHead;
}
};
3. 测试代码
code
#include val << endl;
// node = node->next;
//}
ListNode* reverHead = ReverseList(head);
ListNode* newNode = reverHead;
//while (newNode)
//{
// cout <<"reverNode"<< newNode->val<
// newNode = newNode->next;
//}
return 0;
}
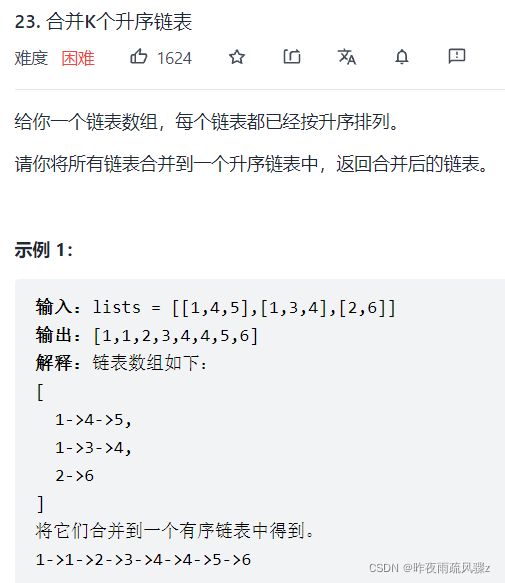
10. 合并K个升序链表
### 解题思路
这道题的合并,主要是利用了递归+归并这两种方法解决了k个的问题。
分治法的思想借网上的说法就是:
1.分解:将原问题分解成为性质一样的若干子问题。
2.解决:解决子问题,并递归求解子问题的问题。问题足够小的时候可以直接求解。
3.合并:合并子问题的解.
其实两个链表的合并大家应该都是会的,但需要在这个的基础上再加上归并的思路可能就提升了整个题目的难度了。
### 代码
```cpp
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* mergeKLists(vector<ListNode*>& lists) {
//分治法
if(lists.size()<=0)
return nullptr;
return merge(lists,0,lists.size()-1);
}
private:
ListNode* merge(vector<ListNode*> &lists,int left,int right)
{
if(left>right)
return nullptr;
if(left==right)
return lists[left];
int mid = (left+right)/2;
return mergeTwoList(merge(lists,left,mid),merge(lists,mid+1,right));//细分到只剩一个链表和另一个链表进行合并
}
ListNode* mergeTwoList(ListNode* list1,ListNode* list2)
{
if(!list1||!list2)
return list1?list1:list2;//不是list1为空的话,就一定是list2为空
ListNode* head,*cur;
if(list1->val>list2->val)//先连接上第一个元素
{
head = list2;
list2 = list2->next;
}
else
{
head = list1;
list1 = list1->next;
}
cur = head;
while(list1!=nullptr&&list2!=nullptr)
{
if(list1->val>list2->val)
{
cur->next = list2;//error1:cur->next
list2 = list2->next;
}
else
{
cur->next = list1;
list1 = list1->next;
}
cur = cur->next;
}
if(list1!=nullptr)
cur->next = list1;//error2:cur->next
if(list2!=nullptr)
cur->next = list2;
return head;
}
};
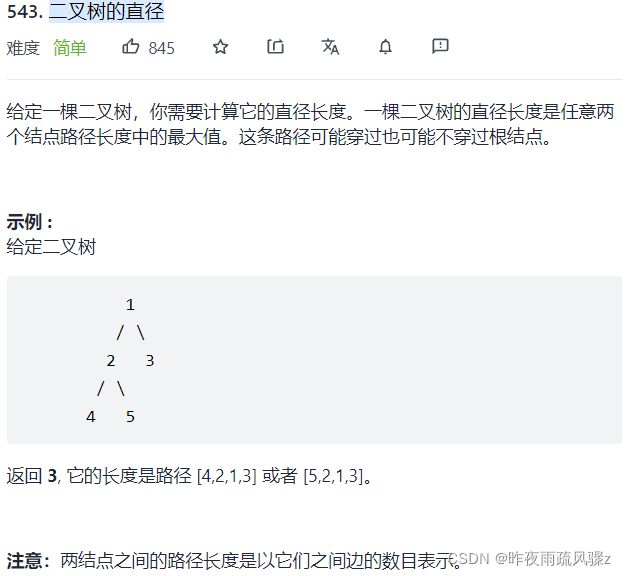
11. 二叉树的直径
code
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int maxValue = 0;
int diameterOfBinaryTree(TreeNode* root) {
if(root==nullptr)
return 0;
dfs(root);
return maxValue;
}
int dfs(TreeNode* root)
{
if(root->left==nullptr&&root->right==nullptr)
return 0;
int left = root->left==nullptr?0:dfs(root->left)+1;
int right = root->right ==nullptr?0:dfs(root->right)+1;
maxValue = max(maxValue,left+right);
return max(left,right);
}
};
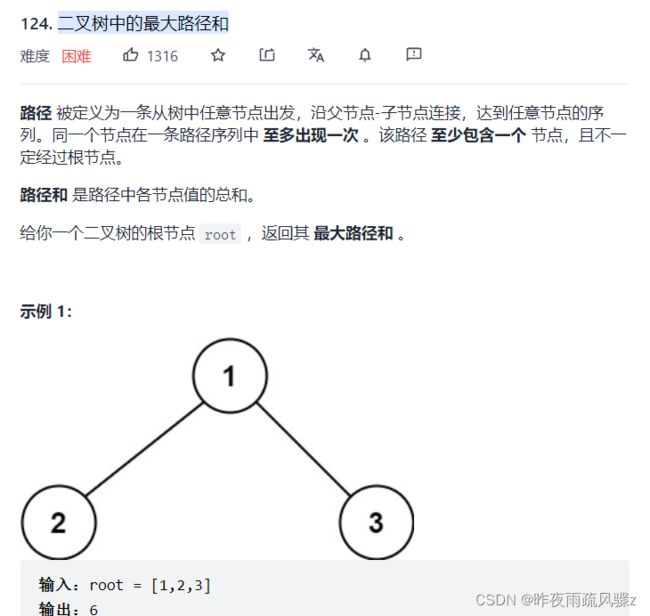
12. 二叉树中的最大路径和
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int maxValue = INT_MIN;
int maxPathSum(TreeNode* root) {
dfs(root);
return maxValue;
}
int dfs(TreeNode* root)
{
if(root==nullptr)
return 0;
int left =max(0,dfs(root->left));
int right =max(0,dfs(root->right));
maxValue = max(maxValue,left+right+root->val);
return max(left,right)+root->val;
}
};
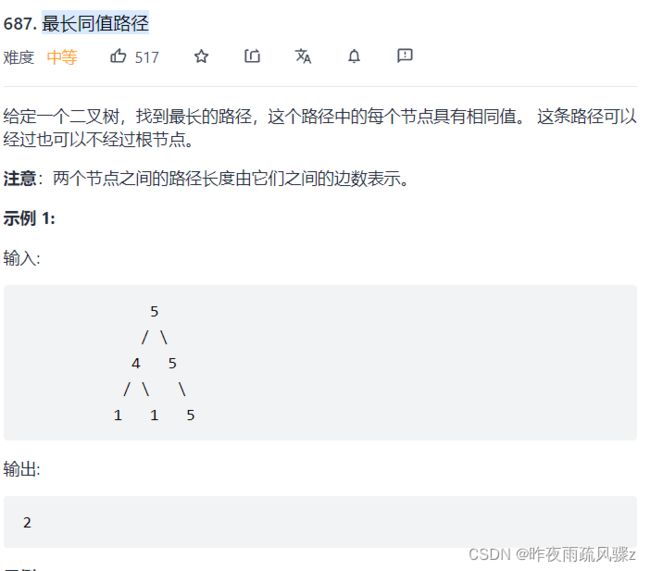
13. 最长同值路径
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int maxValue = 0;
int longestUnivaluePath(TreeNode* root) {
if(root==nullptr)
return 0;
dfs(root);
return maxValue;
}
int dfs(TreeNode* root)
{
if(root->left==nullptr&&root->right==nullptr)
return 0;
//想象成只有3个节点就可以了
int left = root->left==nullptr?0:dfs(root->left)+1;
int right = root->right ==nullptr?0:dfs(root->right)+1;
if(left>0&&root->left->val!=root->val)//如果左子树不等于根节点,那就left=0.
left = 0;
if(right>0&&root->right->val!=root->val)
right = 0;
maxValue = max(maxValue,left+right);//比较的数据就是maxValue与left+right进行相比。
return max(left,right);//这里的返回值,就是让root选择走哪一条路
}
};
参考
- 剑指Offer
- Leetcode 100题