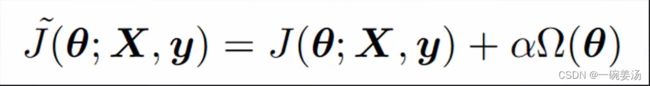深度学习：TensorFlow神经网络理论实战

目录

一、从优化问题讲起

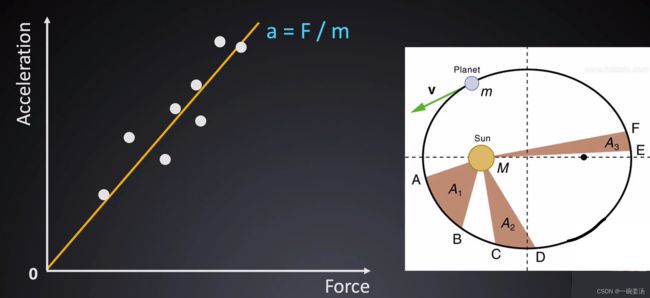
1.1 牛顿与开普勒的对话

1.2 拟合的数学模型

补充：分类的数学模型

1.3 如何通过训练数据优化模型参数

1.3.1 Mini-Batch in Action 

补充 : TensorFlow简介

二、实战：拟合问题

2.1 TensorFlow的安装

2.2 TensorFlow的使用

2.3 TensorBoard可视化界面

2.4 Tensorflow解决拟合问题代码

三、参数优化方法

3.1 随机梯度下降 ( stochastic gradient decent，SGD )

补充知识：梯度

补充知识：如何调节学习速率

3.2 带动量的随机梯度下降 ( SGD w/ momentum ）

3.3 AdaGrad 算法 ( adaptive gradient algorithm )

3.4 Adam 算法 ( adaptive moment estimation )

3.5 小结：

四、实战：优化方法比较

五、深度神经网络

5.1 谁来做特征提取

5.2 激活函数

5.2.1 Sigmoid和Tanh

5.2.2 ReLU激活函数

5.2.3 ReLu变种

5.3 神经网络

5.4.1 神经网络的数学本质

5.4.2 [深度] 学习

六、实战: 使用神经网络建模MNIST数据

小结

七、正则化方法

7.1 欠拟合与过拟合

 7.2 如何评价模型性能

补充:三个集合的选择有何讲究

7.3 常用的正则化方法

7.3.1 增加数据的数量和种类

7.3.2 成本函数增加正则项

7.3.3 Early-Stopping

7.3.4 参数共享

7.3.5 系宗方法

7.3.6 更多方法

7.4 模型训练技巧

7.5 一言以蔽之：大模型 +正则化 > 小模型

补充：如何低成本获得更多训练数据

补充：神经网络的超参数

奥卡姆剃刀定律（Occam's Razor）

八、模型性能评价

8.1 具有欺骗性的平均值

8.2 概率分布与直方图

8.3 混淆矩阵

8.4 性能指标

8.5 ROC曲线

---

一、从优化问题讲起

优化问题，也就是让计算机自动化寻找事物规律。

1.1 牛顿与开普勒的对话

牛顿解决了线性拟合的问题，开普勒解决了非线性拟合的问题。

所谓的拟合就是要最大化，或者最小化某一个目标函数。

1.2 拟合的数学模型

• 线性成本函数：
• 非线性成本函数：
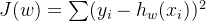
• 目标：

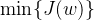
但是分类问题，在拟合问题的基础上，它的标签的取值更加离散。

补充：分类的数学模型

交叉熵：

结合公式和图来看，对于一个标签为1的样本，如果预测的概率比较偏向于0，那么他将获得的惩罚是巨大的，见蓝色线的靠左部分。所以这样的一个成本函数对于分类问题是极其有效的。

1.3 如何通过训练数据优化模型参数

• 蓝色的 Full-Batch：每次进行参数迭代的时候都用所有数据来计算，也就是上述成本函数的求和是对所有的样本进行求和的。好处是平均了所有数据的观点。但其缺点也是非常明显的：就是所有数据点的loss都要预测一遍然后求和，当数据量过大的时候，完全迭代一次可能需要一天的时间，只能对参数进行一次优化。这样从成本上来讲就非常不划算了。
• On-Line：这就是另一种极端，每次只拿一条数据进行参数迭代。好处是一旦数据进来我立马就能迭代更新，数据运算效率极高。缺点是：从统计学上讲，当数据量很少的时候，会存在严重的bias偏差，类似错误的数据可能会把模型带到奇奇怪怪的地方去。所以用这种方法存在很大的风险。一般这种情况是由于产品上线，产品仍需迭代，但是数据产生的速度太慢，只好一条一条地迭代，运用过程中也往往要加上重重数据质量监管。
• Mini-Batch：是对上面两种方法的平衡取舍。一个合适的Batch-size的选取也是一门学问，当Batch-size达到一定程度的时候，会产生推广性能比较差的问题。

1.3.1 Mini-Batch in Action 

1. 每次的iteration，我们会用Mini-Batch大小的数据对模型进行一次优化，随后进入下一个iteration.
2. 当数据快要见底的时候，也就是对整个Full Data进行了接近一次的遍历的时候，再对数据进行一次打乱操作。开始下一个Epoch。
3. iteration描述模型已经看了全量数据的百分之多少，而Epoch则描述了模型看了多少遍全量数据。

补充 : TensorFlow简介

TensorFlow是运用最广的深度学习框架之一。他还有另外一个同行叫做pytorch。他俩的区别就是TensorFlow比pytorch难写不止一点半点。而且TensorFlow它的版本迭代，很多版本之间是互相不兼容的。TensorFlow既服务于科研，又服务于生产。他还是多平台支持的，具有丰富的生态环境。

TensorFlow的运作方式是先构建计算图，这个计算图里面是没有东西的，只有当我们把数据送到里面的时候，开始一个session的计算的时候，他才有数据的流动。所以这跟我们平常的编程模式是有一些差别的。

那么接下里我们将以一个简单的拟合问题的例子向大家展示TensorFlow的基本用法和代码编写。

二、实战：拟合问题

2.1 TensorFlow的安装

安装TensorFlow的时候需要注意python的版本是否适配：本课程用的版本是工程中运用比较广泛的1.12，当然1.14应该也没有任何问题。

TensorFlow版本和python版本的对应配置

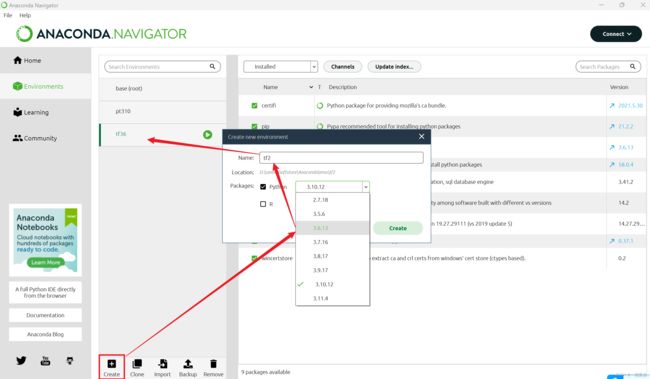
Python虚拟环境的创建Anaconda上操作还是比较简单的，我们搭建深度学习的环境最好是有一个独立的虚拟环境，而不要直接在主环境上搭建。因为我们可能会搭建许多不同版本的环境。学会创建虚拟环境总是必要的。

接下来我们就可以直接在vscode上使用新的Python环境啦（直接切换解释器版本就好了）：

vscode得先安装ipykernel才能使用.ipynb格式文件写代码。（它会自动提示的，install即可）

强烈推荐在Anaconda的主页Home那里安装一个对应环境的powershell或者cmd（我个人觉得这样最能节省点时间然后去学点重要的东西，那些环境切换来切换去的花里胡哨还是别去管的好...）

这里顺便再推荐一款效率神器：Quicker：它能够快速的执行一些常用的软件启动操作或者其他一些动作。我于是就把power shell的启动放在里面啦，按一下ctrl键直接打开Quicker界面：

实际执行安装TensorFlow的语句在powershell中就一条，没什么复杂的，等待安装成功即可：

pip install tensorflow==1.12

执行tf.__version__检验安装完成。 

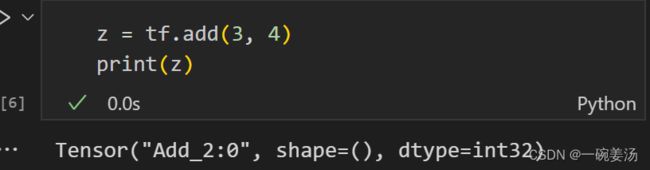
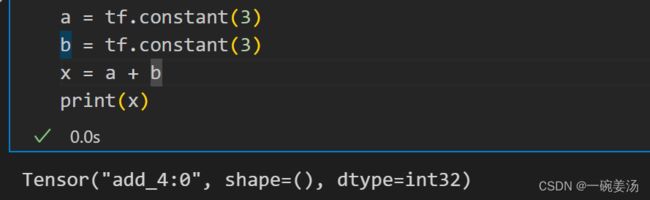
2.2 TensorFlow的使用

我们可以看到z只是一个数据图上的一个节点，里面并没有数据流，也就是没有计算出答案为7

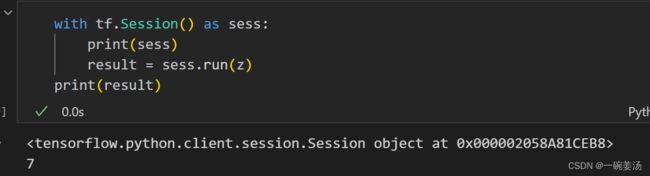
那么怎么对计算图进行运行呢？——可以通过构建一个session，然后run执行。

定义一些常量：

2.3 TensorBoard可视化界面

原理就是：通过一个FileWriter对象把Session内部的graph图结构写到当前文件夹./下的introduction文件里，之后我们利用TensorBoard工具打开的就是这份包含了图结构的tfevents文件。 

这里看到vscode很贴心地帮我们集成了TensorBoard的支持哈哈。

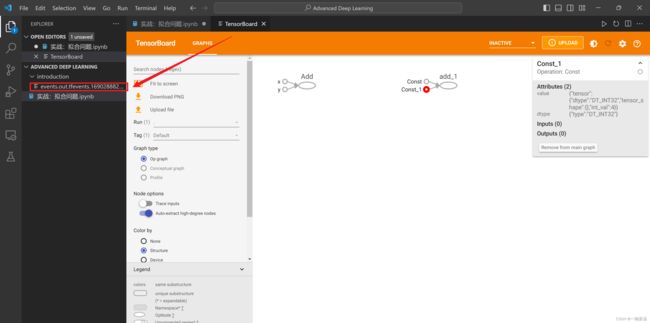
 打开可以看到tensorboard显示的刚才定义的变量以及加法操作的张量Tensor图。

 但是更推荐本地起一个tensorboard的服务，然后用浏览器登录，效果会好很多：

tensorboard --logdir=./basic_mnist --port=9090

使用 tensorboard 的好处：我们一般训练模型的时间是很长的，而 tensorboard 上的界面是在session会话一边写入的时候一边刷新的，所以就相当于，tensorboard给了我们一个自动监控的界面。通过监控界面，你可以实时地看到模型的收敛情况，你可以及时地对这个模型进行干预。

2.4 Tensorflow解决拟合问题代码

接下来我们便来解决如下的一个拟合问题，首先把拟合图像画出来：

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
%pylab inline

train_X = np.asarray([30.0, 40.0, 60.0, 80.0, 100.0, 120.0, 140.0])
train_Y = np.asarray([320.0, 360.0, 400.0, 455.0, 490.0, 546.0, 580.0])
train_X /= 100.0
train_Y /= 100.0

def plot_points(x, y, title_name):
    plt.title(title_name)
    plt.xlabel('x')
    plt.ylabel('y')
    plt.scatter(x, y)
    plt.show()


def plot_line(w, b, title_name):
    plt.title(title_name)
    plt.xlabel('x')
    plt.ylabel('y')
    x = np.linspace(0.0, 2.0, num=100)
    y = w * x + b
    plt.plot(x, y)
    plt.show()

plot_points(train_X, train_Y, title_name='Training Points')

1. 拟合一条直线需要两个参数W和b，这两个参数都属于需要计算的变量，并且需要赋予一个初值才能够进行计算，所以用np.random.randn随机赋予一个初始值。
2. 输入数据是一个需要等到Session会话run的时候才能够放入的量，所以用tf.placeholder来定义他们

n_samples = train_X.shape[0]
X = tf.placeholder('float')
y = tf.placeholder('float')
W = tf.Variable(np.random.randn(), name='weight')
b = tf.Variable(np.random.randn(), name='bias')
y_pred = tf.add(tf.multiply(X, W), b)

 定义模型学习方式：

loss = tf.reduce_sum(tf.pow((y - y_pred), 2)) / (2 * n_samples)
learning_rate = 0.01
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)

模型运行：

import random

def shuffled_X_Y(x, y):
    # 将x和y打包成元组列表
    data = list(zip(x, y))
    # 打乱顺序
    random.shuffle(data)
    # 解包回x和y
    x, y = zip(*data)
    return x, y

training_epochs = 1000
display_step = 50
train_X_copy = train_X 
# 你可能会觉得train_X是个列表，这样赋值是传了个引用，每个epoch要随机打乱样本，若不想改变原数组的话，这样会不会行不通？但经过我的测试发现shuffled_X_Y这个函数返回的会是一个全新的列表。所以这么写是可以的。

train_Y_copy = train_Y

with tf.Session() as sess:
    # 对W,b等随机变量的初始化，不包括待输入的tensor比如tf.placeholder()定义的就需要run的时候指定数据
    sess.run(tf.initialize_all_variables())
    for epoch in range(training_epochs):
        # 补充：这里参数迭代更新采取的策略是On-Line
        for (x_train, y_train) in zip(train_X_copy, train_Y_copy):
            _, cost, current_W, current_b = sess.run([optimizer, loss, W, b],
                                                     feed_dict={X: x_train, y: y_train})
        # 依次epoch结束，随机打乱Full Data
        train_X_copy, train_Y_copy = shuffled_X_Y(train_X_copy, train_Y_copy)

        if epoch % display_step == 0:
            print(('Epoch: %04d | Loss: %.6f | W: %.6f | b: %.6f') %
                  (epoch + 1, cost, current_W, current_b))
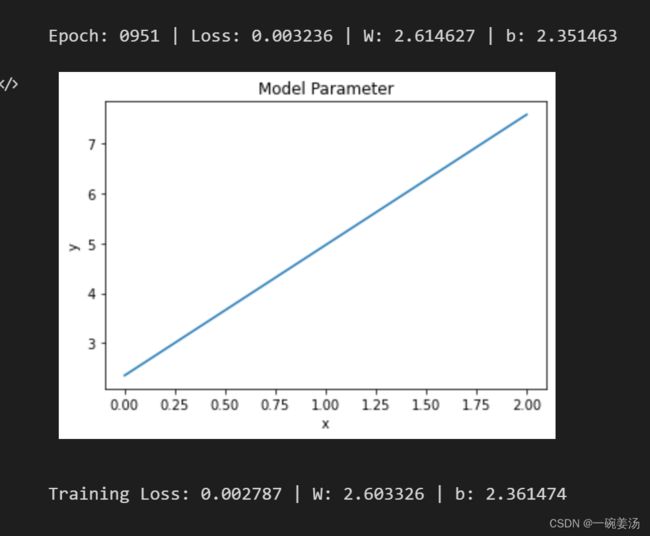
            plot_line(current_W, current_b, 'Model Parameter')
    print(('Training Loss: %.6f | W: %.6f | b: %.6f') %
          (cost, current_W, current_b))

 随着最后一个epoch结束，模型也就跑完了，随后输出结果W = 2.603326，b = 2.361474。

 

从拟合的过程中我们会有不同的参数优化的方法，接下来我们来说不同的优化方法之间的比较。

三、参数优化方法

一阶优化方法：

• 随机梯度下降 ( stochastic gradient decent，SGD )
• 带动量的随机梯度下降 ( SGD w/ momentum ）
• AdaGrad ( adaptive gradient algorithm )
• Adam ( adaptive moment estimation )

二阶优化方法：

• 牛顿法

上面所说的一阶二阶其实就是对成本函数一阶求导或者二阶求导。当然阶数越高，计算量和规模越大，所以二阶的方法几乎不会使用。我们主要集中于一阶的以下四种优化方法。

3.1 随机梯度下降 ( stochastic gradient decent，SGD )

以前我们都叫梯度下降，为什么后来叫随机梯度下降呢？

—— 梯度下降是说我们在计算梯度的时候，把所有的样本数据都用来算梯度，这样算出来的梯度方向无疑更加准确，但是往往运算量太大，承受不起。随机的意思就是说，我随机地抽取一部分，也就是一个Batch-size大小的样本来计算梯度，而不是全部的样本，这样就避免的前面的问题。

这个是它的定义：

• 学习速率：
• 梯度：

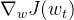
tf.train.GradientDescentOptimizer(lr)

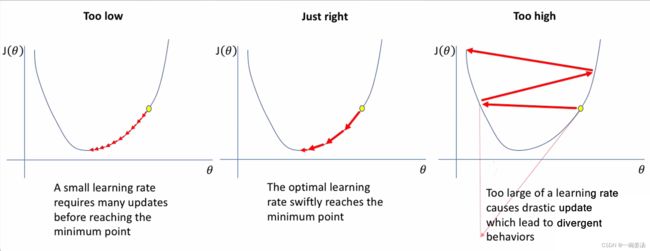
注意：如果学习率很大，那么参数每次迭代更新步长就会很大，如果超过了谷底的宽度，如上图所示，那么小球就会在谷底上方不断震荡，永远掉不到最低面。而学习率太小，又会导致速度太慢。所以学习速率的选取也是一件艺术活：

补充知识：梯度

1. 所谓梯度就是刻画了曲线在各个方向上的曲率。
2. Nabla算子：
3. 注意： 虽然是个映射关系，但不妨把它看作是一个标量，而它的梯度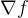是一个向量
4. Nabla算子作用到  这个函数上，是对  这个函数的所有参数求偏导。
5. 梯度刻画的是：在这一个点上，根据他的斜率来计算，哪一个权重的影响是最大的，也就是斜率最大。

补充知识：如何调节学习速率

• 手动调节学习速率：人工观察成本函数的变化 ( Human Intelligence )
• 可变的学习速率：例 : Every k iterations, set α = α * 0.9
• Early Stopping：在正确的时间做正确的事情：当Loss几乎不再继续下降时，尽早把训练过程停掉。(在过拟合欠拟合那里我们会对它作更加深入的了解)

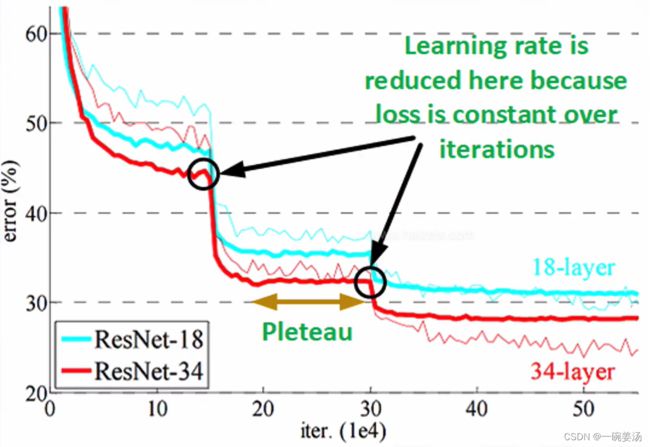
下面是一个典型的成本函数变化趋势图：

可以看到，错误率的曲线呈现了一个阶梯式的下降，原因都是每次在节点处降低了学习率。同时也可以发现它的下降幅度会越来越小：图中第一次下降15%左右，而第二次就只下降了5%都不到，这也提示我们在哪些情况下可以把这个模型停掉。

3.2 带动量的随机梯度下降 ( SGD w/ momentum ）

在论文中：w/ 表示 with ；w/o 表示 without

这个是它的定义：

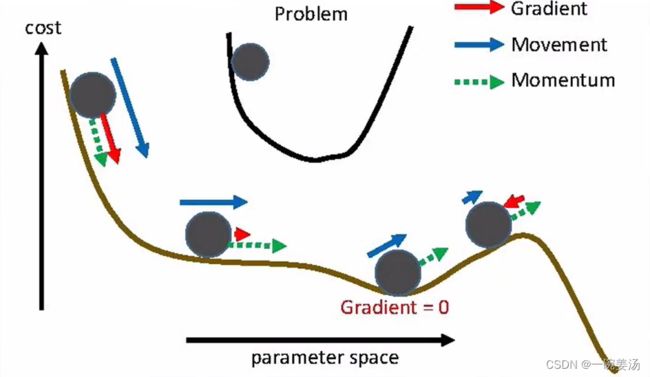
• 随机梯度下降有什么问题呢？——速度太慢，且容易被困在极小值附近，无法真实地模拟小球从高处滚动向下的情景。
• 那么加入动量有什么好处呢？—— 1. 加快梯度下降的过程，可以让小球滚下去地更快。2. 优化效率往往更高，不容易被困在极小值处。

tf.train.MomentumOptimizer(lr, momentum)

3.3 AdaGrad 算法 ( adaptive gradient algorithm )

AdaGrad这种方法虽然工程上很少使用它，但是他为我们带来了一些视野上的开阔，包括目前大家用得非常多的一个Adam算法当中也有借鉴了它的思路。

这个是它的定义：

 相当于，把历史梯度做了一个平方的叠加，然后除到 learning rate - 上，因为  是越来越大的，所以  是越来越小的。额外加上一个  是为了防止除数为 0 的情况。

优点：

• 不需要手动调节学习速率，梯度下降更加稳定。
• 能照顾到梯度小，但对搜索有贡献的维度：因为  的增加不会很大，所以  的减小也不会很大。

缺点：

• 会越来越大，导致训练提前中止。

tf.train.AdagradOptimizer(lr, initial_accumulator_value)

3.4 Adam 算法 ( adaptive moment estimation )

下面是它的定义：

从最后一行我们可以看得出来，Adam算法借鉴了AdaGrad的思路，唯一不同的是，分子处的 m't+1又加入了动量的概念。

tf.train.AdamOptimizer(lr, beta1, beta2, epsilon)

3.5 小结：

我们可以看到，随着参数优化的方法不断地升级，从随机梯度下降到Adam算法，它的表达式是越来越复杂，这样一个复杂带来的好处是：在很多问题上，我们的优化效率会更高，模型越来越好。但是带来的一个直接的后果就是：可能会导致在一些问题上失败，尤其在一些复杂的数据上，Adam经常会失败，比如说训练着训练着，忽然在一个时间点上，它的Loss就变成了NA。那这样的情况怎么去解决呢？

• 一种回避问题的解决办法就是：我不用Adam就是啦。hhh...
• 另外一种办法就是做一个梯度的剪裁：我们为了防止它的梯度变得非常大，我们就加一个上限，超过上限的这部分就按照上限来进行计算。

四、实战：优化方法比较

在网上发现一个开源的梯度下降可视化工具， 大家可以下载来玩一下，感受一下不同参数下的优化方法的特点：

gradient_descent_viz

​

介绍完了优化方法体系，我们接下来就要进入深度学习的最根本的概念的学习。

五、深度神经网络

我们知道机器学习所有的方法都是需要进行特征定义的，通过定义好的特征来进行数据的学习。但是深度学习在很多问题上是不需要预先去做特征提取的，我们只需要把一些领域知识融入到我们的输入当中，尽量保持原始的输入数据，就能够通过模型来对问题进行一个好的建模。这是深度学习和机器学习的一个很大的不同。既然如此我们难免会产生疑问：为什么深度学习能够不进行特征提取就学到更多的东西呢？

5.1 谁来做特征提取

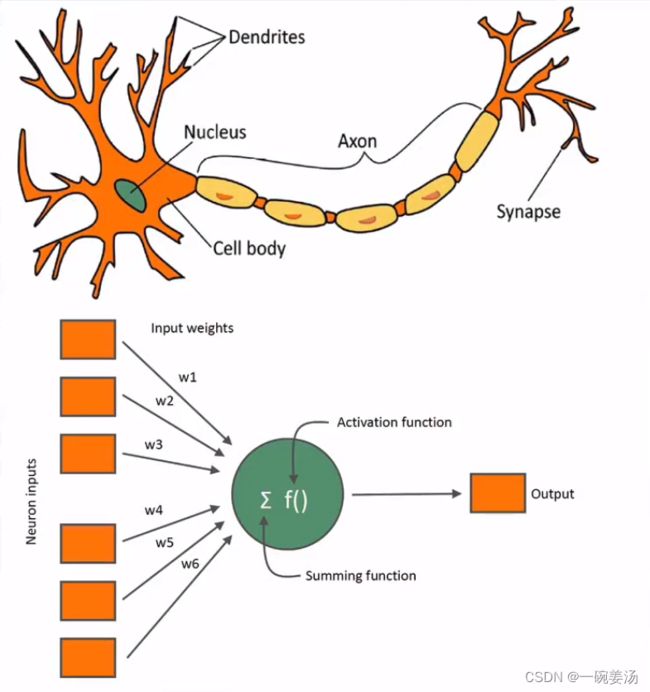
深度学习的基本单元——人工神经元：

我们把生物学上的神经元链接建立成数学模型之后可以看到：每个神经元对连接到该神经元的各个输入信号做了一个加权求和。经过一个激活函数加工过以后，再把信号传递给下一届神经元。

这就是单个神经元所干的事情，运算都很简单。但是当我们把多个神经元组合起来的时候，这些简单的运算就变成了复杂的运算。我们首先先来介绍一下激活函数。

5.2 激活函数

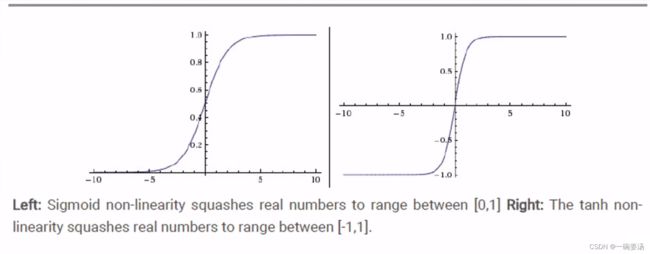
5.2.1 Sigmoid和Tanh

人们的一般直觉是：如果我当前的输出结果太大，会伤害到下一层的神经元，于是便把输入集中到0-1之间或者-1~1之间。早期人们大量使用这两个函数，因为这两个函数形式上很优美。

但是它也有一个巨大的问题：当我们计算这两个函数的导数的时候，当我们x特别的小，落在小于负5的这个区间，它的导数几乎是0。也就是梯度为0，那么优化过程将会停止。这被认为是一个糟糕的现象。为了克服这个问题，人们又提出了ReLU激活函数

5.2.2 ReLU激活函数

 

• 左图中可以看到当x大于0的时候，它的导数一直是有的，于是就不会出现莫名终止的问题。
• 右图中，实线代表ReLU，虚线代表tanh。可以看出ReLU的性能表现还是非常棒的。

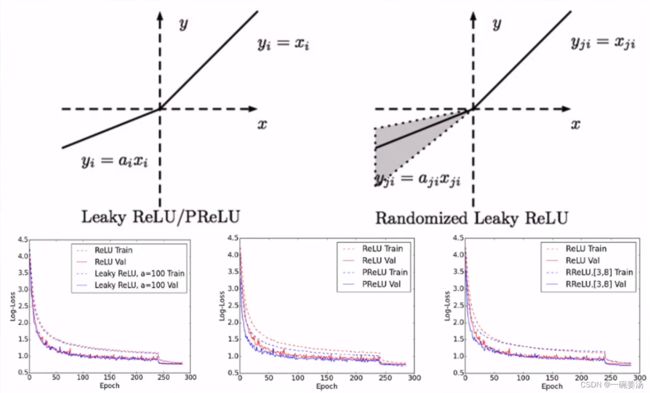
5.2.3 ReLu变种

但是也有人进一步对ReLU函数提出质疑，如果x<0，优化过程依然会是“死的”，于是人们又提出了Leaky ReLU / PReLU：

• 右半边依然不变，左半边变为y=ax。这样，导数就都不为0了。
• 当然我们还可以把a当成参数去学，找到一个好的a。
• 但是优化效果不是很明显：一些数据集上比原来好，另一些数据集上比原来差。所以对于初学者来说，有ReLU足够了。

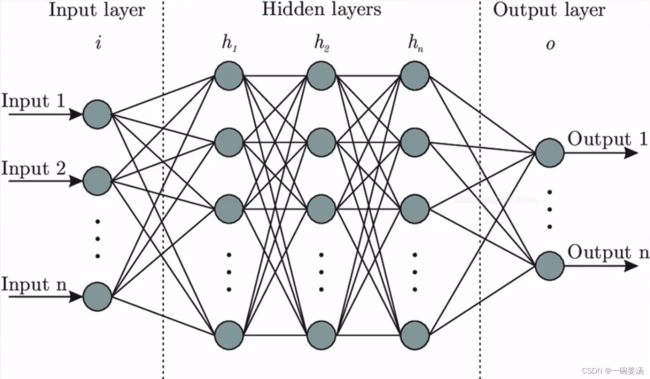
5.3 神经网络

为什么深度学习有那么大的威力？原因就是我们把神经元组合成了神经网络：

神经网络分为三部分：左边是输入，中间是隐藏层，右边是输出。可以看出隐藏层作为计算的单元是神经网络最为关键的部分。层与层之间的神经元相互连接的所有权重w就是我们要学习的参数。

注意：神经元的连接一定是逐层的，比如图中h1的神经元只能连到h2中，而不能连到h3中。

通过神经网络，我们可以把任意的输入，转化为我们想要的输出。我们通常会问多深的神经网络才算深度学习呀，或者多宽？

• 深度：神经网络的层数
• 宽度：一层神经元的个数

其实只要是按照这样的一个思路去进行模型的建立，就是深度学习。

5.4.1 神经网络的数学本质

神经网络的输出：

结论:

神经网络拟合的是一个关于输入的函数！

神经网络比一般的数学建模优势在哪里呢？——我们通过一个非常简单的算法，可以对里面的参数进行自动化的优化，在任何的问题上，只要有足够的数据和标签，我们就可以通过数据来对神经网络参数来进行优化。相当于我们有了一个通用的解决问题的方式。几乎所有的问题，都可以通过这样的一个方式来进行一个自动化的优化。

5.4.2 [深度] 学习

• 理论证明：人们已经通过理论证明了：具有1个隐藏层的神经网络可以拟合任意函数。（宽度可以任意宽）
• 深度的意义：节省指数级的神经元：一个n层的神经网络，可以超过深度为1，宽度为2^n的神经网络。

虽然没有严格的证明，但是关于深度和宽度，有这样一个比较General的结论：

• 更深的网络它的学习能力更强：能够举一反三，将学习到的知识应用到新的领域当中。
• 更宽的网络它的记忆力非常强：能够记住非常多的东西，在类似的场景下能够更快地进行运用。

六、实战: 使用神经网络建模MNIST数据

from tensorflow.examples.tutorials.mnist import input_data
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
%pylab inline

print(tf.__version__)

def imshow(img):
    '''# 显示标签图像'''
    plt.imshow(np.reshape(img, [28, 28]))
    plt.show()

mnist = input_data.read_data_sets('./MNIST_data/', one_hot=True) # 下载数据到./MNIST_data文件夹下

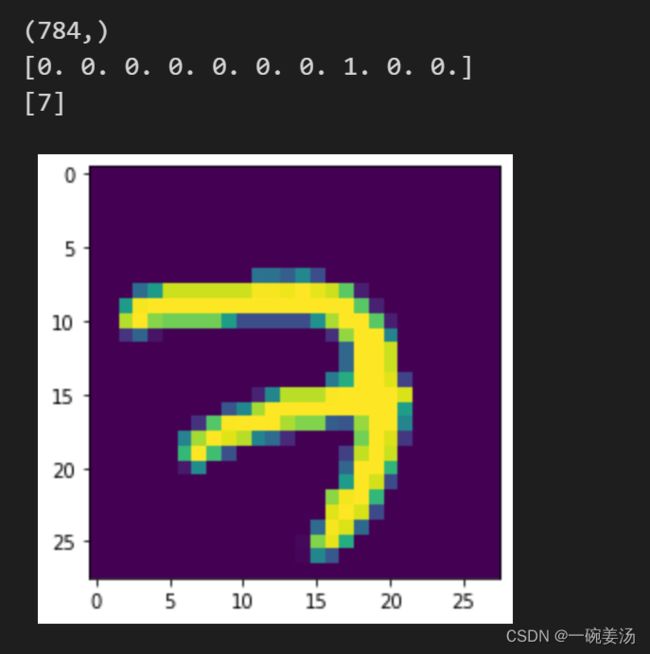
for index in range(10):
    print(mnist.train.images[index].shape)
    print(mnist.train.labels[index])
    print(np.nonzero(mnist.train.labels[index])[0]) # 获取第一个不是0的下标
    imshow(mnist.train.images[index])

def weight_variable(shape):
    initial = tf.truncated_normal(shape, stddev=0.1) # 正态分布，标准差为0.1
    return tf.Variable(initial)
 
def bias_variable(shape):
    initial = tf.constant(0.1, shape=shape) # 避免网络进入假死的状态，不要设为0
    return tf.Variable(initial)

# 定义网络结构
def fcnn(image_batch):
    W_fc1 = weight_variable([784, 200])
    b_fc1 = bias_variable([200])
    W_fc2 = weight_variable([200, 200])
    b_fc2 = bias_variable([200])
    W_out = weight_variable([200, 10])
    b_out = bias_variable([10])
    # hidden_1 = tf.nn.sigmoid(tf.matmul(image_batch, W_fc1) + b_fc1)
    # hidden_2 = tf.nn.sigmoid(tf.matmul(hidden_1, W_fc2) + b_fc2)
    hidden_1 = tf.nn.tanh(tf.matmul(image_batch, W_fc1) + b_fc1)
    hidden_2 = tf.nn.tanh(tf.matmul(hidden_1, W_fc2) + b_fc2)
    _y = tf.nn.softmax(tf.matmul(hidden_2, W_out) + b_out)
    return _y

x = tf.placeholder(tf.float32, [None, 784]) # 预先不知道Batch_size是多少，用None即可
y_ = tf.placeholder(tf.float32, [None, 10]) 
y = fcnn(x)

correct_prediction = tf.equal(tf.argmax(y_, 1), tf.argmax(y, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
cross_entropy = tf.reduce_mean(tf.reduce_sum(-y_ * tf.log(y + 0.00000001), reduction_indices=[1])) # 0.00000001是为了避免log0的情况导致计算溢出；1代表class这个维度；0代表Batch-size这个维度
train_step = tf.train.GradientDescentOptimizer(0.01).minimize(cross_entropy)

# 为了在tensorboard中展示出每个iteration的情况：包括loss和accuracy的变化。
tf.summary.scalar('loss', cross_entropy)
tf.summary.scalar('accuracy', accuracy)
merged = tf.summary.merge_all()

training_iteration = 50000
batch_size = 64
display_step = 50
with tf.Session() as sess:
    writer = tf.summary.FileWriter('./basic_mnist/', sess.graph)
    sess.run(tf.initialize_all_variables())
    for iteration in range(training_iteration):
        batch_xs, batch_ys = mnist.train.next_batch(batch_size)
        summary, _, current_accuracy = sess.run([merged, train_step, accuracy], feed_dict={x: batch_xs, y_:batch_ys})
        writer.add_summary(summary, iteration)
        if iteration % display_step == 0:
            print('Iteration: %5d | Accuracy: %.6f' % (iteration + 1, current_accuracy))
    print('Test Accuracy: %.6f' % sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels}))
    writer.close()
    

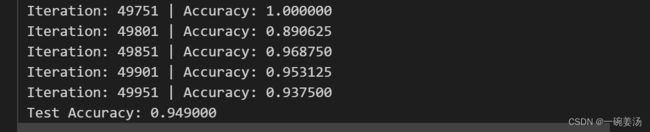
为探究不同的激活函数对于对于整个网络训练的影响，下面是用tanh激活函数训练出来的网络：

• 可以看到，仅仅通过更换一个激活函数，Accuracy就从93%提高到97%，还是一个挺令人振奋的变化。

下面是同样用sigmoid的激活函数的情况下，更换momentum优化算法：

•  可以看到，使用带动量的随机梯度下降优化效果也有一定的提升。

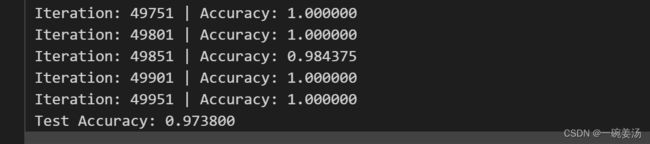
下面使用我们的大BOSS——Adam优化算法：

• Adam算法的优化过程收敛速度极快。而且最终效果也达到了恐怖的97%，98%左右的Accuracy基本上已经到达了全连接神经网络在MNIST数据集上的极限。

小结

所以说做深度学习像是一个炼丹的过程，从业人员俗称炼丹师。就是因为有太多的方法和参数可以调节。在平时的学习过程中，我们就可以有意识地去用一个记事本记录下所有的随着参数变化的结果趋势。这些都将成为日后工作当中的宝贵的经验。

七、正则化方法

通过以上的编程训练，相信大家能够对神经网络以及TensorFlow的具体实现有了比较深入的认知。

相信大家会有一个疑问，就是我们在训练模型的过程中，为什么要把MNIST这个数据集分为两个部分：训练集和测试集。而且训练集和测试集的关系一定要是相互独立的。也就是模型在训练过程中应该没见过测试集。原因就是我们希望训练的模型能够具备更好的推广性能。

这就涉及到了过拟合的概念。

• 过拟合：模型在训练集上的表现非常好，但是在测试集上的表现却很糟糕。换句话说，模型记忆了训练集预测的内容，但是这种记忆在新的数据集上其实没有丝毫用途。
• 而正则化方法就是通过一些手段能让模型在训练之后变得更加具有可推广性。换句话说就是能让模型变得更加鲁棒。

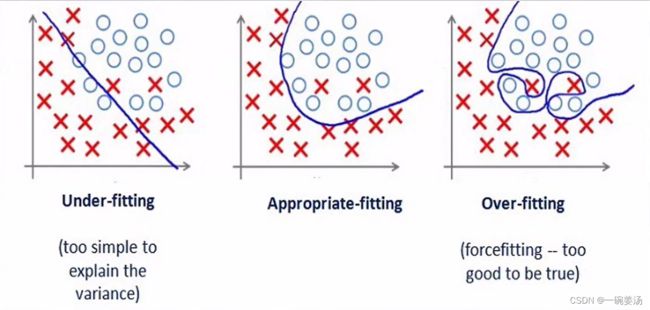
7.1 欠拟合与过拟合

拟合问题：

欠拟合的原因：模型本身的智商不够，或者训练的iteration不够，或者训练的数据不够，模型没有学到应有的知识。

分类问题：

 7.2 如何评价模型性能

• 验证集是用来调参的：确定模型最好的参数结构。
• 测试集是用来模型最终的测试，是一个完全独立的数据集，在模型训练阶段是完全不可见的。

补充:三个集合的选择有何讲究

• 数据分布具有代表性:保证三者分布相同，需要随机化（举个例子：你不能让学语文的同学去做数学题）
• 时间方向：预测未来的情形，一定不可在时间维度进行随机化
• 数据冗余：确保训练集与测试集数据不相关，不能有冗余数据

7.3 常用的正则化方法

使用正则化的方法解决过拟合问题，我们可以往以下三个方面来下功夫：数据、优化方法、和模型。

7.3.1 增加数据的数量和种类

• 获取更多的训练数据
• 人工合成更多的数据
• 使用生成对抗网络生成假数据

上述方法实现：对数据的空间变换，学习数据生成Pattern;...

• 在训练数据中加入各种噪声（注意一定不能是违背模型鲁棒性的）

增加噪声是为了：增加模型的反脆弱性。

7.3.2 成本函数增加正则项

•   权重系数：代表施加正则化的强度
•  有两种常用的范式：Lasso就是把所有权重的绝对值加起来；而Ridge是把权重的平方加起来求根号。这两种方式在数学统计上会有完全不同的表现：L1-Norm会带来稀疏的参数空间，里面只有少量的非零参数，好处就是当你想分析哪些因素是对最终预测的贡献较大时，它能够明确地给你答复。而Ridge方法的特点就是可以限制参数的范围，把参数往0的方向压，而且使参数分布尽量地平均。

有了这样的一种直觉（intuition）后，面临方法的选择时能够更加有的放矢。

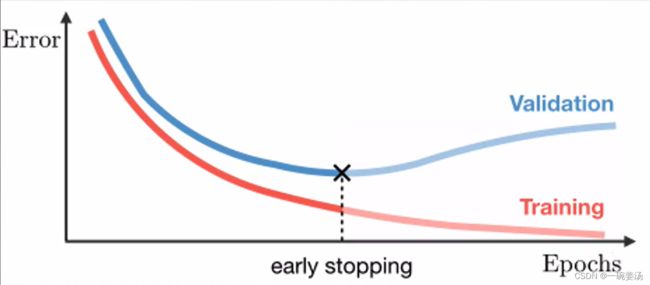
7.3.3 Early-Stopping

当我们发现验证集上的Loss不降反增的时候，我们把它停掉，模型的iteration是刚刚好的。

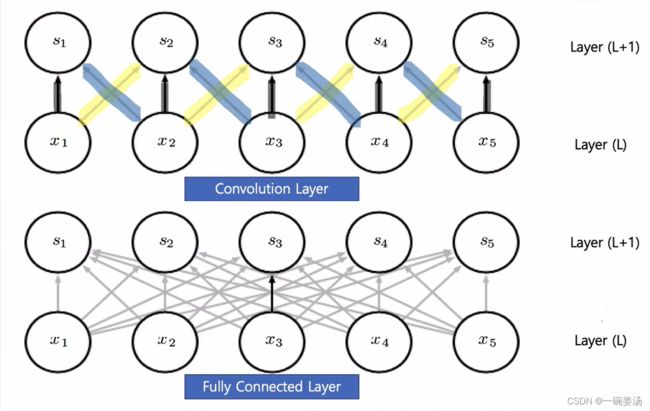
7.3.4 参数共享

全连接神经网络很容易导致参数的直接暴涨。卷积神经网络中，进行了有选择的链接，也就是参数共享。大幅度地减少了参数的数目，而且参数的运行效率会更高：更重要的参数能够发挥它的作用，这样模型能够把注意力真正放在与图像识别相关的这些参数上面去。

• 卷积神经网络是空间维度上的参数共享，循环神经网络是时间维度上的参数共享。

7.3.5 系宗方法

最典型的就是Dropout：

用一句话概括：就是当家做主人。模型训练过程中会屏蔽掉一部分神经元。让剩余部分的神经元当家做主来投票。看能做出来什么样的预测。然后在下一轮的迭代过程中又会扔掉另外一批的神经元来预测。

这么做有什么好处？——他每个神经元都能够独立地去做出更好的判断。可能有些神经元偷懒，我邻居太强了，我就不要做任何判断了。那OK我强制把邻居关起来，你自己来上，看你行不行。在这种情况下，每个神经元就有比较好的鲁棒性。能够做出来更好的判断。

为什么叫系宗方法？——系宗方法是通过多种模型投票去决定最后的一个结果，但是可以看到这里只是一个模型，我们是通过屏蔽的方法模拟了这么一种系宗模型。

除了鲁棒性的增加之外，在未来的应用当中还有一个好处，大家可以把每个神经单元看成一个计算单元。当我有一个计算单元挂了的时候，就相当于这个计算单元被屏蔽了，但是他的邻居还能够当家做主，继续工作。这样的一个系统鲁棒性自然也会更强。所以通过Dropout可以显著地提高全连接神经网络的鲁棒性。

7.3.6 更多方法

• 多任务学习（图像分类的同时，进行目标检测，强制网络具备多面手的能力，减少网络偷懒的可能性，过拟合可以看作网络在学习上偷了懒取巧了）
• Batch Normalization
• 非监督/半监督学习（都是为了增加任务的难度，强迫模型去学习更多的东西）
• 生成式对抗网络
• ...

7.4 模型训练技巧

首先确认训练数据是没问题的!

• 训练误差大 ?

更大的模型;训练更长时间; 更好的模型结构:

• 测试误差大 ?

更多的数据;正则化; 更好的模型结构

7.5 一言以蔽之：大模型 +正则化 > 小模型

补充：如何低成本获得更多训练数据

• 众包标注 ( 适用于容易的任务，比如道路识别 )
• 使用数据增强的方法
• 使用生成对抗网络生成假数据

补充：神经网络的超参数

• 学习速率
• 正则化参数
• 神经网络的层数
• 每一个隐层中神经元的个数
• Epoch数
• Batch Size
• 输出神经元的编码方式
• 成本函数的选择
• 权重初始化的方法
• 神经元激活函数的种类

奥卡姆剃刀定律（Occam's Razor）

如无必要，勿增实体：Entities should not be multiplied unnecessarily

八、模型性能评价

对于一个客观的统计学评价我们需要有哪些指标呢？让我们来一探究竟。

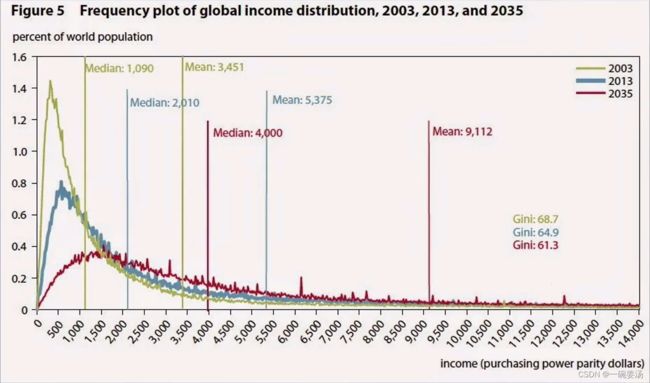
8.1 具有欺骗性的平均值

通过上面这张收入水平分布图可以看出，近似成一个幂律分布。富人拉高了平均值水平。在这里相比于平均值，中位数是一个更好的指标。但其实还有一个更好的选择：直方图

8.2 概率分布与直方图

 通过一个直方图我们可以很轻松地把数据分布给画出来（对数据分布有认识这是一件很重要的事情）可以看出大部分人的收入水平集中在：50-150之间。

8.3 混淆矩阵

对于分类问题一个最好的判断标准就是画出混淆矩阵。第一个字母T代表True，预测正确，F代表False，预测错误。第二个字母P代表阳性，N代表阴性。

举一个医学上的例子：肺癌患者。TP代表模型捕捉到了肺癌患者。TN代表模型正确排除了不是肺癌的患者。FP则代表患者本身不是肺癌，但是模型认为他是肺癌，假阳性，这是可接受的。但是FN就非常可怕了，患者本身是肺癌，但是模型认为他不是，这种情况叫漏诊。

不同的问题中会赋予不同的格子不同的权重。

8.4 性能指标

• Precision：精确度（所有被模型抓出来的正例中到底有多少是正例）
• Sensitivity：敏感度/召回率（所有患者中，有多少是被模型识别出来的，漏诊的程度）
• Specificity：特异性
• Accuracy：准确率

到底多少个独立的指标可以确定一个模型的完整性能？——三个。

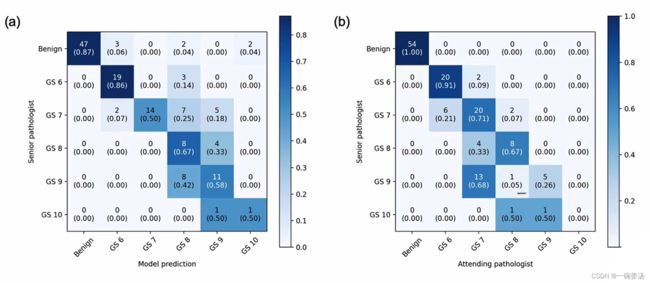
多分类混淆矩阵：

对于多分类任务来说，我们看混淆矩阵希望，都能够达到靠近主对角元不要太多。每一行的求和都是1.

8.5 ROC曲线

• 模型在预测的时候预测出来其实是一个概率，是一个连续的值。但是我们在画混淆矩阵的时候是取他其中的一个cutoff（阈值），这样才能把混淆矩阵画出来。但是我们在比较两个模型的性能我们更希望去遍历它整个不同的cutoff的值，从0一直遍历到1，来看一下他在整个阈值空间上整体的表现。在统计上我们是得到不同的分类阈值下的Sensitivity和Specificity的组合。
• 图中可以看到，人的平均水平是黑色的五角星，是低于ROC曲线的，可以理解为人的平均水平不如AI的。
• 同时我们把ROC曲线下方的面积——AUC也作为模型性能的一个客观指标。
• 另外可以看到，当1-Specifity达到0.38的时候，Sensitivity是能够达到1的。也就是说，我们可以在保证不漏诊的情况下，使1-Specifity达到0.38的水平。