【python】贝叶斯优化包bayesian-optimization

官方文档 https://github.com/bayesian-optimization/BayesianOptimization/tree/master

以下是机翻：

使用高斯过程的贝叶斯全局优化的纯 Python 实现。

安装：

pip install bayesian-optimization

这是一个基于贝叶斯推理和高斯过程构建的约束全局优化包，试图以尽可能少的迭代次数找到未知函数的最大值。该技术特别适合高成本函数的优化，在勘探和开发之间的平衡很重要的情况下。

---

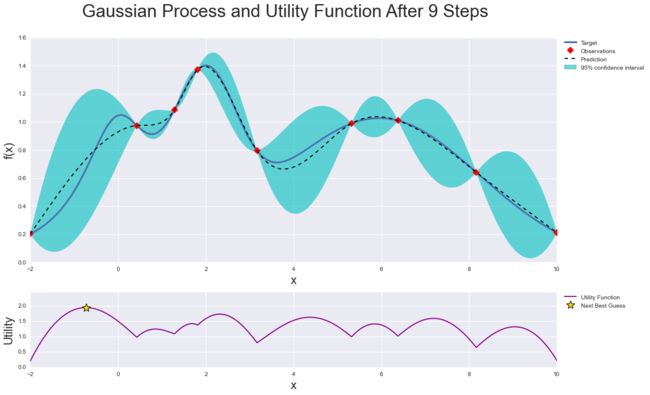
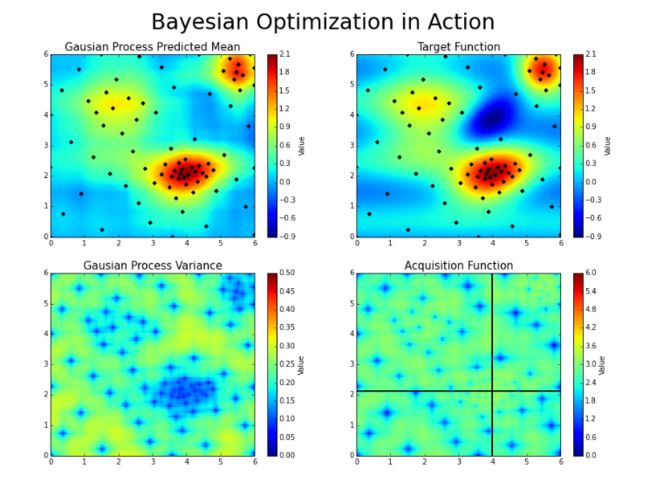
贝叶斯优化的工作原理是构建最能描述要优化的函数的函数后验分布（高斯过程）。随着观测数量的增加，后验分布得到改善，算法变得更加确定参数空间中的哪些区域值得探索，哪些区域不值得探索，如下图所示。

当您一遍又一遍地迭代时，算法会考虑其对目标函数的了解，平衡其探索和利用的需求。在每个步骤中，高斯过程都会拟合已知样本（之前探索的点），后验分布与探索策略（例如 UCB（置信上限）或 EI（预期改进））相结合，用于确定下一个应该探索的点。

此过程旨在最大限度地减少找到接近最佳组合的参数组合所需的步骤数。为此，该方法使用代理优化问题（找到采集函数的最大值），尽管仍然是一个难题，但更便宜（在计算意义上）并且可以使用通用工具。因此，贝叶斯优化最适合对要优化的函数进行采样是一项非常昂贵的工作的情况。有关此方法的正确讨论，请参阅参考资料。

贝叶斯优化包的基本浏览

1.指定要优化的函数

 

这是一个功能优化包，所以第一个也是最重要的成分当然是要优化的功能。

免责声明：我们确切地知道以下函数的输出如何取决于其参数。显然这只是一个示例，您不应该期望在真实场景中了解它。但是，应该清楚的是您不需要这样做。为了使用这个包（更一般地说，这个技术），你所需要的只是一个f接受一组已知参数并输出一个实数的函数。

def black_box_function(x, y):
    """Function with unknown internals we wish to maximize.

    This is just serving as an example, for all intents and
    purposes think of the internals of this function, i.e.: the process
    which generates its output values, as unknown.
    """
    return -x ** 2 - (y - 1) ** 2 + 1

 

2. 入门

我们需要开始的就是实例化一个BayesianOptimization对象，指定要优化的函数f及其参数及其相应的边界pbounds。这是一种受约束的优化技术，因此您必须指定每个参数可以探测的最小值和最大值才能使其发挥作用

from bayes_opt import BayesianOptimization

# Bounded region of parameter space
pbounds = {'x': (2, 4), 'y': (-3, 3)}

optimizer = BayesianOptimization(
    f=black_box_function,
    pbounds=pbounds,
    random_state=1,
)

BayesianOptimization 对象开箱即用，无需太多调整。您应该注意的主要方法是maximize，它的作用正是您所认为的。

您可以传递许多参数来最大化，但最重要的是：

• n_iter：您要执行多少步贝叶斯优化。步数越多，就越有可能找到合适的最大值。
• init_points：您想要执行多少步随机探索。随机探索可以通过使探索空间多样化来提供帮助。

optimizer.maximize(
    init_points=2,
    n_iter=3,
)

|   iter    |  target   |     x     |     y     |
-------------------------------------------------
|  1        | -7.135    |  2.834    |  1.322    |
|  2        | -7.78     |  2.0      | -1.186    |
|  3        | -19.0     |  4.0      |  3.0      |
|  4        | -16.3     |  2.378    | -2.413    |
|  5        | -4.441    |  2.105    | -0.005822 |
=================================================

可以通过属性访问找到的参数和目标值的最佳组合optimizer.max。

print(optimizer.max)
>>> {'target': -4.441293113411222, 'params': {'y': -0.005822117636089974, 'x': 2.104665051994087}}

而所有探测参数的列表及其相应的目标值可通过 property 获得optimizer.res。

for i, res in enumerate(optimizer.res):
    print("Iteration {}: \n\t{}".format(i, res))

>>> Iteration 0:
>>>     {'target': -7.135455292718879, 'params': {'y': 1.3219469606529488, 'x': 2.8340440094051482}}
>>> Iteration 1:
>>>     {'target': -7.779531005607566, 'params': {'y': -1.1860045642089614, 'x': 2.0002287496346898}}
>>> Iteration 2:
>>>     {'target': -19.0, 'params': {'y': 3.0, 'x': 4.0}}
>>> Iteration 3:
>>>     {'target': -16.29839645063864, 'params': {'y': -2.412527795983739, 'x': 2.3776144540856503}}
>>> Iteration 4:
>>>     {'target': -4.441293113411222, 'params': {'y': -0.005822117636089974, 'x': 2.104665051994087}}

2.1 改变边界

在优化过程中，您可能会意识到为某些参数选择的界限是不够的。对于这些情况，您可以调用该方法set_bounds来更改它们。您可以传递现有参数及其关联的新边界的任意组合。

optimizer.set_bounds(new_bounds={"x": (-2, 3)})

optimizer.maximize(
    init_points=0,
    n_iter=5,
)

|   iter    |  target   |     x     |     y     |
-------------------------------------------------
|  6        | -5.145    |  2.115    | -0.2924   |
|  7        | -5.379    |  2.337    |  0.04124  |
|  8        | -3.581    |  1.874    | -0.03428  |
|  9        | -2.624    |  1.702    |  0.1472   |
|  10       | -1.762    |  1.442    |  0.1735   |
=================================================

2.2 顺序域约简

有时，为问题指定的初始边界太宽，并且添加点来改善解域区域中的响应面是无关的。其他时候，成本函数的计算成本非常高，而最大限度地减少调用次数是非常有益的。

当值得快速收敛到最佳点而不是尝试找到最佳点时，随着搜索的进行收缩当前最佳值周围的域可以大大加快搜索进度。使用SequentialDomainReductionTransformer问题的边界可以动态平移和缩放，以尝试提高收敛性。

域缩减笔记本SequentialDomainReductionTransformer中显示了使用的示例。有关该方法的更多信息可以在论文“On the Robustness of a simple Domain Reduction Scheme for Simulation-Based Optimization”中找到。

3、指导优化

通常情况下，我们知道函数最大值可能位于参数空间的区域。对于这些情况，BayesianOptimization对象允许用户指定要探测的点。默认情况下，这些点将被延迟探索 ( lazy=True)，这意味着这些点将仅在您下次调用时进行评估maximize。这个探测过程发生在高斯过程接管之前。

参数可以作为字典或可迭代对象传递。

optimizer.probe(
    params={"x": 0.5, "y": 0.7},
    lazy=True,
)

optimizer.probe(
    params=[-0.3, 0.1],
    lazy=True,
)

# Will probe only the two points specified above
optimizer.maximize(init_points=0, n_iter=0)

|   iter    |  target   |     x     |     y     |
-------------------------------------------------
|  11       |  0.66     |  0.5      |  0.7      |
|  12       |  0.1      | -0.3      |  0.1      |
=================================================

4. 保存、加载和重启

verbose>0默认情况下，您可以通过在实例化对象时进行设置来跟踪优化的进度BayesianOptimization。如果您需要对日志记录/警报进行更多控制，则需要使用观察者。有关观察员的更多信息，请查看高级游览笔记本。这里我们只会看到如何使用本机对象JSONLogger保存和加载文件进度。

4.1 保存进度

from bayes_opt.logger import JSONLogger
from bayes_opt.event import Events

观察者范式的工作原理是：

1. 实例化观察者对象。
2. 将观察者对象与优化器触发的特定事件联系起来。

该BayesianOptimization对象在优化期间会触发许多内部事件，特别是每次它探测函数并获得新的参数-目标组合时，它都会触发一个Events.OPTIMIZATION_STEP事件，我们的记录器将侦听该事件。

警告：记录器不会回顾之前探测过的点。

logger = JSONLogger(path="./logs.log")
optimizer.subscribe(Events.OPTIMIZATION_STEP, logger)

# Results will be saved in ./logs.log
optimizer.maximize(
    init_points=2,
    n_iter=3,
)

默认情况下，json 文件中以前的数据将被删除。如果您想继续使用同一个记录器，则应将reset参数JSONLogger设置为 False。

4.2 加载进度

当然，如果您存储了进度，您将能够将其加载到BayesianOptimization. load_logs最简单的方法是从子模块调用该函数util。

from bayes_opt.util import load_logs


new_optimizer = BayesianOptimization(
    f=black_box_function,
    pbounds={"x": (-2, 2), "y": (-2, 2)},
    verbose=2,
    random_state=7,
)

# New optimizer is loaded with previously seen points
load_logs(new_optimizer, logs=["./logs.log"]);