高斯羽流模型的简明原理以及python代码实现（针对卫星监测的气体点源排放建模）

高斯羽流模型

高斯羽流模型(Gaussian Plume Model)是被广泛用来描述在静稳大气中点源排放的气体浓度分布的模型

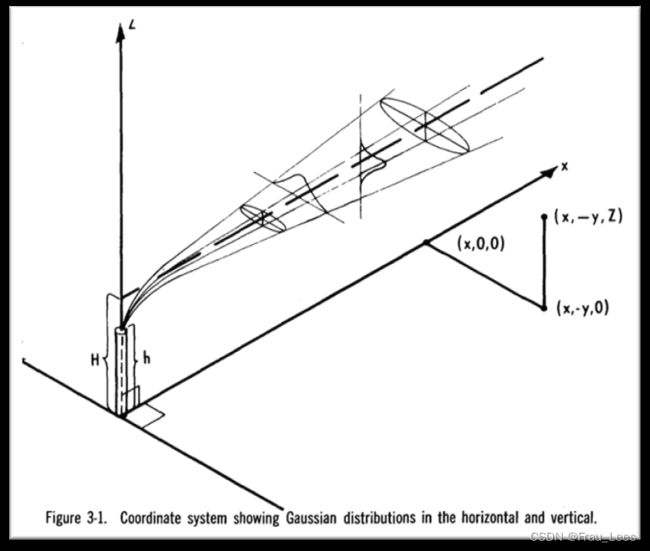
对于满足以下四点的的大气污染物排放，高斯羽流模型可以较为便捷地估算出排放羽流中任意一点的气体浓度。
①风的平均流场稳定，风速均匀，风向平直；
②y、z轴方向符合正态分布；
③污染物在输送扩散中质量守恒；
④污染源的源强均匀、连续

高斯羽流模型的一般形式为下式，

其中，坐标系的x轴方向为顺风方向，C为任意坐标为(x,y,z)的点通过模型计算出的浓度，Q为气体排放速率，U为风速，y为点的y坐标，即横风距离，z为点的z坐标。σ_y和σ_z分别为y方向和z方向上的大气扩散参数。
不难发现，这个公式是由Q和其余部分组成的，排放速率Q和风速U与浓度C直接相关，而公式的其余部分规定了羽流的高斯形状

对于一个立体的羽流，从正面观察到的是在z方向上的累积分布，这个分布是对立体羽流在y方向上的积分，可以用这样的公式来描述羽流形状，

从俯视方向观察到的是在y方向上的分布，这个分布是对立体羽流在z方向上进行了积分，可以用这样的公式来描述羽流形状，

将这两个平面公式相乘就得到了第一个立体公式。

由于需要将高斯羽流模型用于对卫星数据监测到的气体排放事件，而卫星观测到的气体浓度是在垂直柱上的柱浓度，因此使用俯视方向上的模型即可。
并且不需要考虑高架点源排放时出现的地面反射，因为不管z方向上出现了多少变化，都已经统一积分在一个平面里了。

大气扩散参数

有关大气扩散参数σ_y 和 σ_z的计算，有很多种不同的计算方法。这二者都是与大气稳定度和风向距离x的函数，这些以米为单位的系数可以用Pasquill- Gifford-Turner划分的大气稳定程度估算得到：
σ_y=ax^b
σ_z=cx^d+f

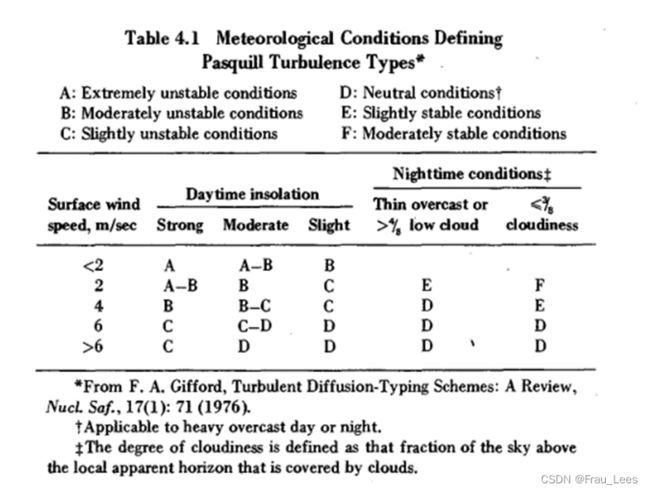
在Bruce Turner的大气扩散模型技术手册里，两张图分别绘制了在A-F六种大气稳定性环境下，大气扩散参数σ_y 和 σ_z与顺风距离x的关系：


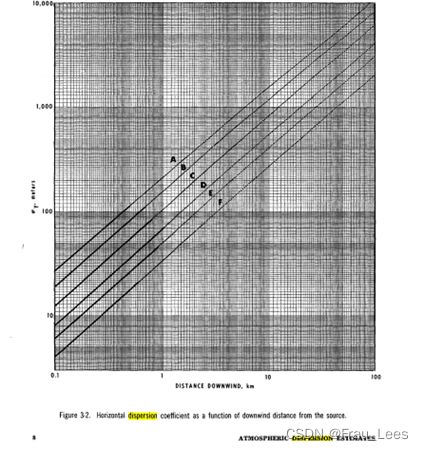
另外，Briggs(1973)结合了Pasquill、BNL和TVA曲线(x = 10 km范围内的观测值)，使用了关于公式的渐近极限的理论概念，得出了表4.5中给出的广泛使用的一组公式:

在Delance O. Martin的*Comment On"The Change of Concentration Standard Deviations with Distance"*一文中，作者总结了Turner，McMullen’s equations，和自己利用下表的a,c,d,f参数计算的实验结果，发现结果非常相似，在不同的扩散距离下σ_y和σ_z的值都很接近。

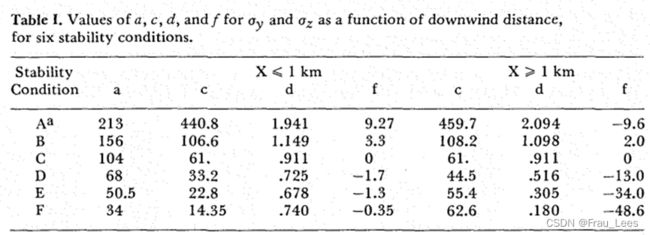
而 *Comment On"The Change of Concentration Standard Deviations with Distance"*一文中指出b为常数，为0.894。

python代码实现

第一步，编写计算σ_y的函数，参数a和b参考Nassar(2021)和上文内容：

import numpy as np
import sys

def new_calc_sigmas(CATEGORY, x1):
    x = np.abs(x1)

    a = np.zeros(np.shape(x))
    b = np.zeros(np.shape(x))

    if CATEGORY == 'A':
        a = 213
        b = 0.894
    elif CATEGORY == 'B':
        a = 184.5
        b = 0.894
    elif CATEGORY == 'C':
        a = 150
        b = 0.894
    elif CATEGORY == 'D':
        a = 130
        b = 0.894
    elif CATEGORY == 'E':
        a = 104
        b = 0.894
    elif CATEGORY == 'F':
        a = 23.3
        b = 0.625
    elif CATEGORY == 'G':
        a = 77.6
        b = 0.813
    else:
        sys.exit()

    sig_y = a * ((x/1000) ** b)

    return(sig_y)

第二步，编写羽流函数：

import numpy as np
from new_calc_sigmas import new_calc_sigmas


def gaussian_fuc(Q, u, windir, x, y, xs, ys, STABILITY):
    u1 = u
    x1 = x - xs # x，y为羽流中任意一点,xs,ys为排放源位置
    y1 = y - ys # 将排放源位置转移至坐标原点

# 气象学的风向是从正北方向开始，沿顺时针方向转到风来的方向，
# 通过以下两行可将风速分解到正北y和正东x方向
    ux = u1 * np.sin((windir - 180.) * np.pi / 180.)
    uy = u1 * np.cos((windir - 180.) * np.pi / 180.)
# 为了计算顺风距离和横风距离，需要计算风向与原点与任意羽流点连线的夹角，
# 这里采用向量相乘的方法计算，向量相乘再除以模长相乘，就得到夹角的cos值
    dot_product = ux * x1 + uy * y1
    magnitudes = u1 * np.sqrt(x1 ** 2. + y1 ** 2.)

    subtended = np.arccos(dot_product / (magnitudes + 1e-15)) # 夹角
    hypotenuse = np.sqrt(x1 ** 2. + y1 ** 2.)

    downwind = np.cos(subtended) * hypotenuse # 顺风距离
    crosswind = np.sin(subtended) * hypotenuse # 横风距离
    ind = np.where(downwind > 0.)
    C = np.zeros((len(x), len(y)))


    sig_y = new_calc_sigmas(STABILITY, downwind)

    C[ind] = Q / (np.sqrt(2. * np.pi) * u1 * sig_y[ind]) * np.exp(-crosswind[ind] ** 2. / (2. * sig_y[ind] ** 2.))
    return C

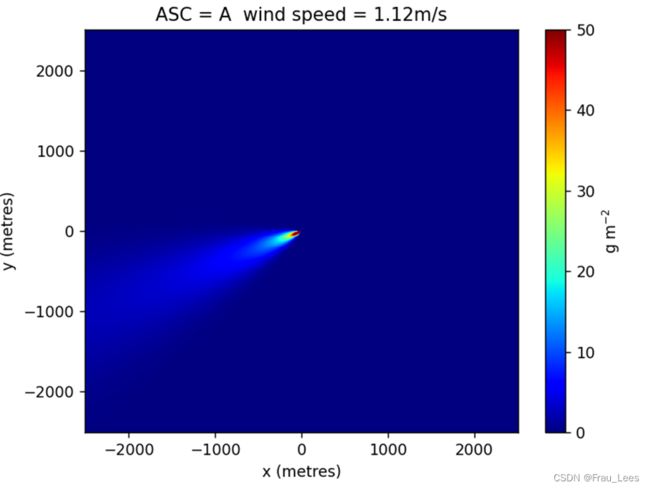
最后一步，可以在程序中调用编写好的Gaussian函数，来生成指定x,y范围内，指定风速风向和排放源坐标的气体浓度的平面累积分布。
例如，在风向为68°，风速为1.12m/s时，生成的高斯羽流如下图所示。

参考资料：
https://www.tandfonline.com/doi/pdf/10.1080/00022470.1976.10470238
[1]Bruce Turner, D. (2020). Workbook of Atmospheric Dispersion Estimates : An Introduction to Dispersion Modeling, Second Edition. Workbook of Atmospheric Dispersion Estimates. https://doi.org/10.1201/9780138733704
[2]Hanna, S. R., Briggs, G. A., & Hosker, R. P. Jr. (1982). Handbook on atmospheric diffusion. https://doi.org/10.2172/5591108
[3]Hu, Y., & Shi, Y. (2021). Estimating CO2 Emissions from Large Scale Coal-Fired Power Plants Using OCO-2 Observations and Emission Inventories. Atmosphere, 12(7). https://doi.org/10.3390/ATMOS12070811
[4]Liu, X., Godbole, A., Lu, C., Michal, G., & Venton, P. (2015). Optimisation of dispersion parameters of Gaussian plume model for CO2 dispersion. Environmental Science and Pollution Research, 22(22), 18288–18299. https://doi.org/10.1007/S11356-015-5404-8/TABLES/5
[5]Martin, D. O. (2012). Comment On"The Change of Concentration Standard Deviations with Distance". Http://Dx.Doi.Org/10.1080/00022470.1976.10470238, 26(2), 145–147. https://doi.org/10.1080/00022470.1976.10470238
[6]Newman, J. F., & Klein, P. M. (2014). The Impacts of Atmospheric Stability on the Accuracy of Wind Speed Extrapolation Methods. Resources 2014, Vol. 3, Pages 81-105, 3(1), 81–105. https://doi.org/10.3390/RESOURCES3010081
[7]Pasquil, F. (1961). The Estimation of the Dispersion of Windborne Material. Meteorological Magazine
https://www.jianshu.com/p/5cf580af2def