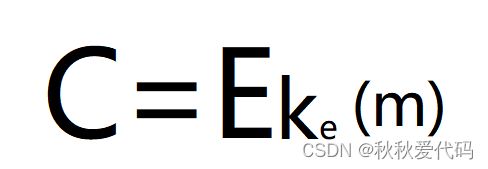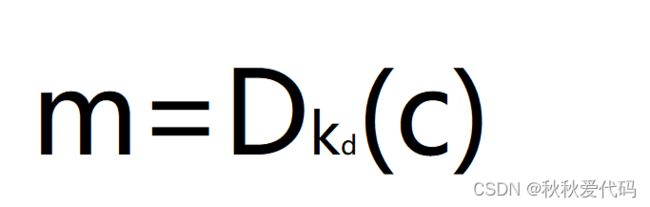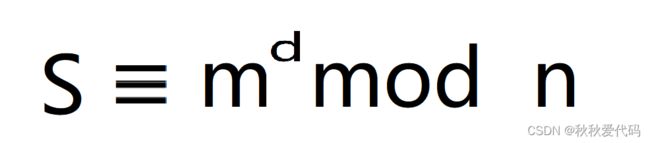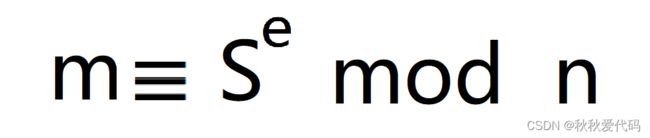【密码学补充知识】
密码学概述
1.基本概念
明文 : 要交换的信息
密文 : 明文经过一组规则变换成看似没有意义的随机消息。
加密 : 明文经过一组规则变换成密文的过程
解密 : 密文恢复出明文的过程
加密和解密都需要一个密钥来完成。
根据密钥的特点,密码体制可以分文两类
对称密码体制(单钥密码体制): 加密密钥和解密密钥相同,或者从一个密钥很容易推导出另外一个密钥。密码需要保密,所以对称密码体制又叫私钥密码体制
非对称密码体制 (双钥密码体制,公钥密码体制): 加密密钥和解密密钥不相同,并且从一个密钥很难推导出另外一个密钥。加密密钥可以公开,所以非对称密码体制又叫公钥密码体制
2.密码体制
一个密码体制通常包括5部分
(1) 明文空间 M :全体明文m的集合;
(2) 密文空间 C : 全体密文c的集合;
(3) 密钥空间 K : 全体密钥的集合 ; 在具体的一次加密过程中,加密密钥ke和解密密钥kd都来自该空间,密钥空间不同密钥的个数称为密码体制的密钥量,通常来说:密钥量越大,密码体制的安全强度越高。
(4) 加密算法 E : 由加密密钥控制的加密交换的
(5) 解密算法 D : 由加密密钥控制的加密变换的集合。
一个密码体制要满足一致性,即如果
那么
安全性要求
保密性:信息只为授权用户使用,不能泄漏给未授权的用户。
完整性:信息在传输或者储存过程中,不能被偶然或者蓄意地破坏(删除,修改,伪造,重放,插入等)和丢失。
认证性:确保通信方的确是服务方认证地那位。
认证方法分为: 实体认证和消息认证。实体认证指的是 确认一个实体的身份;消息认证 指的是 确认一个消息地来源。(arp欺骗就是破坏了认证性)
不可否认性:防止通信方对以前的许诺或者行为否认
密码分析(攻击方法)
(1)穷举分析:
通过试遍密钥空间中的所有密钥来对密文进行界面,直至得到正确的明文。
应对方法: 增加密钥空间的密钥量,但是也只能增加密码体制的安全强度,不能绝对安全。
(2)统计分析攻击
通过分析明文和密文的统计规律来破译密码体制。
该方法对破译古典密码体制很有效,但是相应的也有其他密码体制。
(3)数学分析攻击
针对加解密算法的数学基础和密码学性质,通过数学求解的方法来破解密码体制
密码体制评估
(1)无条件安全性
如果一个具有无限计算资源的敌手都不能破译一个密码体制,则这种体制是无条件安全的。一次一密方法在唯密文攻击下可以达到无条件安全,但是一次一密是指每次加密一个信息 的时候都用不同的密钥,会消耗高额的密钥分配成本。 显然不实用。
(2)计算安全性
如果使用最好的算法来破译一个密码体制所需要的计算代价远远超过敌手的计算资源,则成这个体制是计算安全的。
(3)可证明安全性
如果一个密码体制的安全性可以规约为 某个数学问题,且这个数学问题是难解的,则这个密码体制是可证明安全的。
☞ 现代密码学的目标
(1) 一个密钥可以重复使用,不是每次使用后就更换新的密钥
(2) 一个短密钥可以加密长明文,密钥的长度比明文短。
也就是说,在大多数情况下,我们只要保证计算安全性即可
2.数字签名
基本概念
产生原因:
在电子世界,人们希望用某种方法代替手写签名,实现对数字信息的签名。
数字签名的特性:
※(1)不可伪造性: 除了签名者,任何人不能伪造签名者的合法签名。
※(1)认证性:接收者相信这份签名来自签名者。
※(1)不可重复使用性:一个消息的签名不能用于其他信息
※(1)不可否认性: 签名者事后不能否认自己的二千米
※(1)不可修改性:一个消息在签名后不能被修改。
分类:
按用途分:
=》普通数字签名
=》具有特殊用途的数字签名(如: 盲签名)
=》不可否认签名
=》群签名
=》代理签名
按是否具有消息恢复功能
=》具有消息恢复功能的数字签名
=》不具有消息恢复功能的数字签名
按是否使用随机数
=》确定性数字签名
=》随机化数字签名
RSA数字签名
RSA密码体制可以用来加密,也可以用于数字签名
1.参数与密钥生成
(1)选取两个保密的大素数 p,q 。
(2)计算 n=pq ,Ψ(n)=(p-1)(q-1),其中Ψ(n)是n的欧拉函数值。
(3)随机选取证书e ,1 (4)计算d ,满足de=1 mod Ψ(n) 。 (5)公钥为 (e,n) 私钥为 d 。 对于消息m∈Zn,签名为 对于消息签名对 (m,e) ,如果有 则 s 是 m的有效签名 让验证者(V: Verifier)相信正在与之通信的另一方(P:Prover)就是所称的那个实体,目的是方式假冒。 一个安全的身份识别协议应该满足三个条件 : (1)P 能向 V 证明 他的确是P (2)P向V证明身份后,V没有获得任何有用测定信息,P不能假冒成 V (3)除了P以外的第三者 以P的身份执行该协议,能够让V相信他是P的概论可以忽略不记。 (想到ARP欺骗没 (*^_^*) ) 身份识别分为 两类: (1)弱识别 : 使用口令、口令段、口令驱动的密钥来证明自己的身份 (2)强识别 :通过向验证者展示与证明者实体有关的秘密信息来证明自己的身份。这种识别通常通过挑战-应答方式进行,挑战是指一方随机地选取一个秘密数发送给另一方,而应答是对挑战的回答。应答与实体的秘密信息及对方挑战有关系。 1988年, Guillou 和 Quisquater 提出了基于 RSA 密码体制安全性的身份识别方案。 1.系统初始化2.签名
3.验证
3.身份识别
概念
Guillou-Quisquater身份识别方案
Guillou - Quisquater 身份识别方案需要一个信任权威 TA 。 TA 选择两个大素数计算 n = pq ,确定自己的签名算法  和 Hash 函数 h 。 TA 还要选取一个长度为40bit 的素数 b 作为自己的公钥,计算私钥
和 Hash 函数 h 。 TA 还要选取一个长度为40bit 的素数 b 作为自己的公钥,计算私钥  公开参数为 n 、 b 、 h 、
公开参数为 n 、 b 、 h 、
2. TA 向 P 颁发身份证书
(1) TA 为 P 建立身份信息 IDp 。
(2) P 秘密选取一个整数 u ,0≤ u ≤ n -1且 ged ( u , n )=1,计算: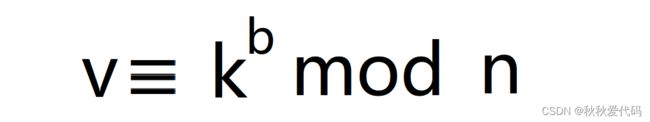
并将 v 发送给 TA 。
(3) TA 计算签名 s = SigTA ( IDp , v ),将证书 C ( P )=( IDp , v , s )发送给 P 。
3.P向 V 证明其身份
(1) P 随机选取整数 k ,1≤ k ≤ n -1,计算: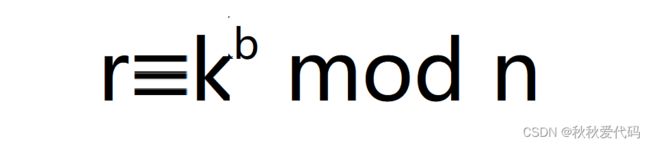
并将证书 C ( P )和r发送给 V 。
(2) V 验证 s 是否是 TA 对( IDp , v )的签名。如果是, V 随机选取整数 r ,0≤ r ≤ b -1,
并把它发送给 P 。
(3) P 计算: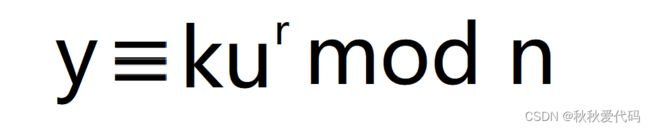
并将 C(p) 和y发送给 V 。
(4) V 验证是否有: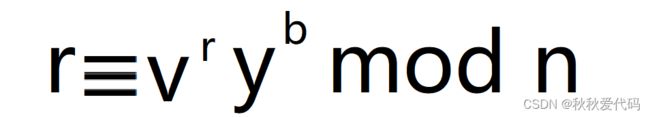
成立。如果成立, V 就接受 P 的身份证明;否则拒绝 P 的身份证明
在 Guillou - Quisquater 身份识别方案中,由于 P 掌握了秘密信息 u ,对于任何挑战,
P 都可以在步骤(3)中计算 y 使得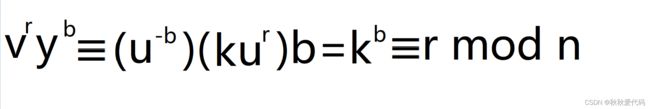
成立。如果一个攻击者 C 能够猜测出 V 随机选取的整数 r ,则 C 可以任意选取一个 y ,计算: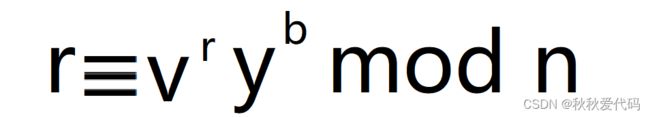
在步骤(1)中, C 将 y 发送给 V ,在步骤(3)中, C 将 y 发送给 V 。最后,在步骤(4)中, V -定能够验证: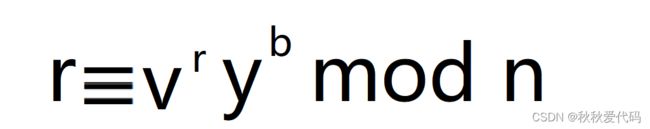
成立, V 接受 C 的身份证明,从而 C 成功地冒充了 P 。攻击者 C 能够猜测随机数,的概率为1/b。因为6是一个很大的整数,所以 C 想成功冒充 P 的概率非常小。