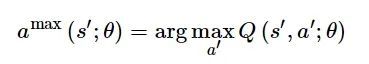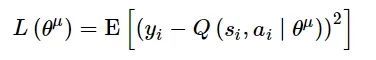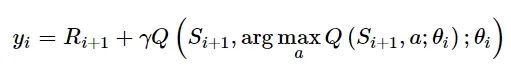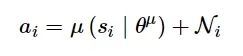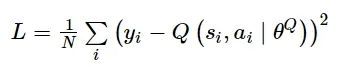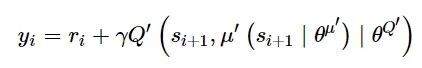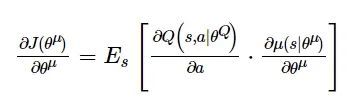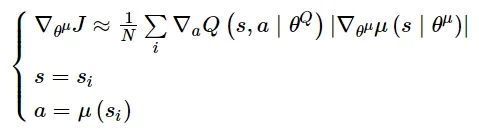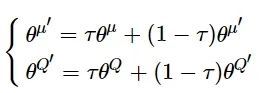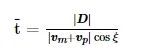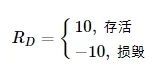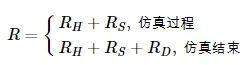基于深度强化学习算法的无人机智能规避决策

源自：系统工程与电子技术

作者：吴冯国  陶伟  李辉  张建伟  郑成辰.

“人工智能技术与咨询”   发布

摘 要

为提升无人机在复杂空战场景中的存活率, 基于公开无人机空战博弈仿真平台, 使用强化学习方法生成机动策略, 以深度双Q网络(double deep Q-network, DDQN)和深度确定性策略梯度(deep deterministic policy gradient, DDPG)算法为基础, 提出单元状态序列(unit state sequence, USS), 并采用门控循环单元(gated recurrent unit, GRU)融合USS中的态势特征, 增加复杂空战场景下的状态特征识别能力和算法收敛能力。实验结果表明, 智能体在面对采用标准比例导引算法的导弹攻击时, 取得了98%的规避导弹存活率, 使无人机在多发导弹同时攻击的复杂场景中, 也能够取得88%的存活率, 对比传统的简单机动模式, 无人机的存活率大幅提高。

关键词

深度强化学习 ; 无人机 ; 单元状态序列 ; 门控循环单元

引言

现代空战环境错综复杂, 空空导弹和机载雷达性能不断提升, 超视距空战已经在现代空战中占据主导地位[1], 空空导弹也早已成为打击空中单位的主要武器。无人机作为空中战场的理想作战目标之一, 被普遍运用到军事领域当中[2]。利用无人机可持续大机动的飞行特点, 采取高效的机动策略以提高无人机对导弹的规避、逃逸成功率, 对提升无人机的空战生存能力而言至关重要[3]。

无人机规避空空导弹问题一直都是空战的研究热点。王怀威等[4]采用蒙特卡罗方法验证了无人机实施常规盘旋机动规避导弹的效果。Imado等[5]利用微分对策法研究导弹与无人机差速博弈的问题。另外, 还有诸多针对导弹的规避方式[6-10]、规避效能评估[11-13]以及无人机最优或次优规避策略解析解[14-16]等方面的研究。以上方法依赖于完备的空战对战模型以求解在单枚导弹打击情况下的最优机动策略, 当导弹数量变化时, 模型很难理解, 而且建立空战对战模型本身就是一个非常复杂的过程, 需要使用大量微分函数结合积分函数，才能表征无人机与导弹状态属性的转移规律。

深度强化学习(deep reinforcement learning, DRL)算法在马尔可夫决策过程(Markov decision process, MDP)基础上, 采用端到端学习方式, 以态势信息为输入, 直接利用神经网络获取输出, 控制智能体作出决策, 被广泛应用于自动化控制当中[17-22]。范鑫磊等[23]将深度确定性策略梯度(deep deterministic policy gradient, DDPG)算法[24]应用于无人机规避导弹训练, 在简易模型下对固定态势攻击的空空导弹进行仿真验证。宋宏川等[25]针对导弹制导规则设计成型奖励, 用DDPG算法训练无人机规避正面来袭的导弹, 对比典型规避策略, 训练出了仅次于置尾下降机动的逃逸策略。

上述研究表明, 无人机能够通过特定的机动方式来规避空空导弹的打击, 而深度强化学习算法可以训练出自动规避空空导弹的智能体。总体而言, 以往研究大多基于单枚导弹打击场景。但是在超视距空战中, 多枚导弹从不同方向锁定无人机并发动协同攻击的情况屡见不鲜。在这种情形下, DRL算法会存在状态空间维度大, 状态信息维度不断变化, 神经网络输入维度难以固定, 算法收敛性能差等问题。

针对以上问题, 本文提出一种基于单元状态序列(unit state sequence, USS)的强化学习算法(reinforcement learning method based on USS, SSRL)。在该算法中，首先，将导弹和无人机进行一对一的特征编码，形成特征单元; 其次，根据距离优先级对所有编码后的特征单元进行排序, 组合成一个USS; 然后，使用门控循环单元(gated recurrent unit, GRU)对USS中的特征单元进行特征融合, 提取其中的隐藏特征信息; 最后，将隐藏特征信息看作该时刻的状态信息，并将信息传入强化学习算法的神经网络。将该算法分别应用于深度双Q网络(double deep Q-network, DDQN)[26]和DDPG算法上, 在公开无人机空战博弈仿真平台上进行训练。仿真结果表明, 由SSRL算法训练的智能体能够学到连续规避机动策略, 控制无人机进行规避导弹机动, 增加导弹脱靶量, 提升无人机连续规避导弹的成功率。

1 相关理论

1.1  MDP

强化学习训练过程类似于人类学习, 即智能体在不断探索和获取外界反馈中学习能够获得的最大利益, 通常被建模成MDP[27]。MDP由状态空间S、动作空间A、状态转移函数P和奖励函数R组成：状态空间是所有可能的状态集合; 动作空间是所有可能的动作集合; 状态转移函数则描述了在当前状态下采取某个动作后到达下一个状态的概率；奖励函数用于描述在当前状态下采取该行动所获得的奖励[28]。

1.2  DDQN算法

强化学习任务通常是时间序列决策问题, 与训练数据高度相关。文献[29]引入经验重放机制, 降低数据之间的相关性, 使样本可重复利用, 提高学习效率。DDQN算法使用两个神经网络，将动作选择和值函数估计进行解耦, 评估网络Q用于环境交互, 用于动作选择的公式如下:

(1)

目标网络Q′用于估计下个状态值函数, 通过最小化损失函数, 更新评估网络参数, 使训练过程更加稳定:

(2)

式中: yi代表目标值, 即:

1.3  DDPG算法

DDPG算法基于确定性策略梯度[30](deterministic policy gradient, DPG)算法, 并将DDQN中的双重网络机制应用到ActorCritic框架, 分别使用参数为θμ、θμ′、θQ和θQ′的深度神经网络拟合策略评估函数μ、策略目标函数μ′、动作值评估函数Q和动作值目标函数Q′。

策略评估函数负责与环境交互, 从环境中获取状态S、奖励r、结束标识d, 进行动作选择如下:

(3)

式中: Ni 为动作噪声, 对噪声使用模拟退火[31]以避免陷入局部最优, 同时增加了算法的探索能力。

智能体通过最小化损失公式，以更新值评估网络参数:

(4)

式中: yi为目标动作值。即:

(5)

根据DPG算法的理论证明策略函数关于θμ的梯度等价于动作值函数关于Q(s, a|θQ)的期望梯度, 使得可以以梯度更新策略评估网络:

(6)

因此，策略评估网络按照此方向更新网络参数：

(7)

动作值网络参数在更新过程中又用于计算策略网络的梯度, 软更新方式为

(8)

以减少学习过程中动作值网络可能出现的不稳定性。

1.4 GRU网络

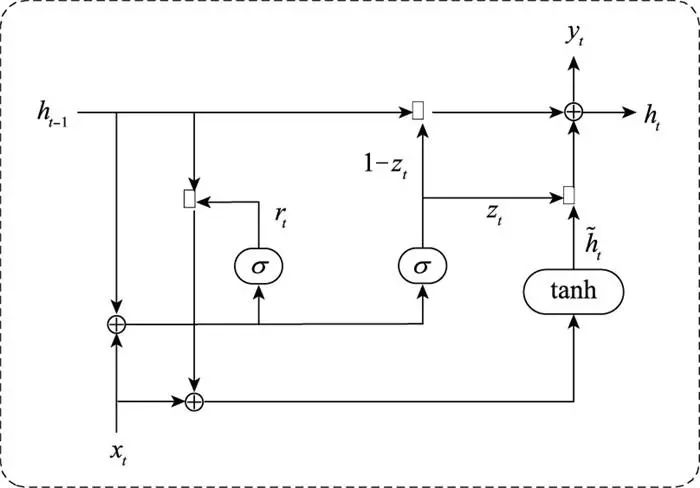
循环神经网络(recurrent neural network, RNN)[32]能够处理时序型输入, 以序列x在t时刻的数据xt和前t－1时刻神经网络的输出ht－1作为输入, 输出yt和ht, ht又作为之后的输入。这种结构能结合历史信息, 具有前瞻能力。GRU[33]是改进的RNN, 其网络结构如图 1所示, 更新门zt和重置门rt将新的数据与历史信息相结合并选择遗忘某些历史信息。GRU网络能够解决传统RNN在长期记忆和反向传播中梯度消失的问题, 与长短期记忆(long-short term memory, LSTM)网络收敛效果相当, 并且在训练速度上有很大程度的提升。

图1   GRU网络

2 SSRL算法

在超视距空战中, 通常以机载雷达、地面雷达及红外瞄准跟踪装置等进行目标探测, 其战场范围太大, 作战的实体数目难以确定, 经常以多机、多目标协同作战方式出现[34]。当无人机面临多枚导弹的协同打击时, 环境中的实体数量会发生动态变化, 神经网络在训练时需要按照最大实体数目输入全部环境信息, 实体信息默认值为零, 存在的实体按实际状态值进行填充。这种方式适用于实体数目确定的场景, 且并非所有的环境信息都会对当前智能体的决策产生影响。如何有效地获取空战环境中的态势特征, 筛选出更加重要的状态信息[35-36], 对提升训练效果而言十分重要。

USS编码方式能够有效解决这个问题。在自然语言处理中, 不同的单词被转换成等长的稠密向量, 用于区分各个单词之间的差异, 而RNN能够从词向量模型中提取特征信息。借鉴词向量编码的优势, 考虑将智能体与单个目标视为一组特征映射, 进行状态编码, 提取其中的重要态势特征, 并将其编码为状态单元。该时刻的USS由多个状态单元组成, 利用GRU网络高效训练和融合序列信息的能力, 从USS中提取隐藏特征, 用于强化学习。这种特征提取方法在理论上可以结合到在单实体对多目标(可变)的任意场景中, 属于通用解决方案。本文将USS结合到DDQN和DDPG算法中, 在超视距空战中连续规避导弹的场景下进行实验。

2.1  USS

单元状态序列的编码过程如下。

步骤1 从仿真环境中获取无人机观测信息Of和导弹的观测信息O, O=(o1, o2, …, on)。

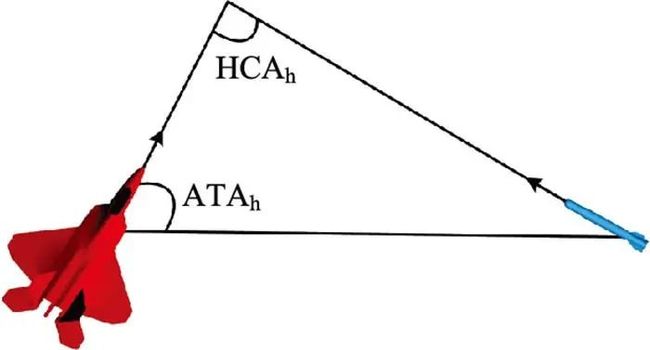
步骤2 将无人机与每一枚敌方空空导弹的观测信息沿水平面和垂直平面分别进行分解, 并使用天线偏转角(antenna train angle, ATA)和航向交叉角(heading crossing angle, HCA)描述其朝向和位置差异。ATAh和HCAh分别表示水平面的天线偏转角和航向交叉角, 如图 2所示。

图2   水平面态势分解

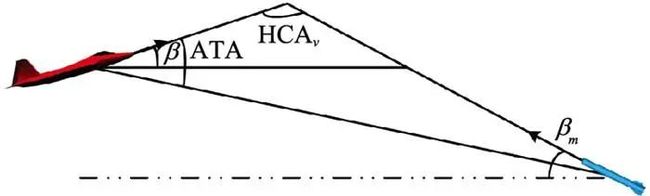
ATAv和HCAv分别表示无人机运动垂直切面的天线偏转角和航向交叉角, β表示飞机俯仰角, βm表示导弹俯仰角, 如图 3所示。

图3   垂直面态势分解

步骤3 根据无人机与每一枚敌方空空导弹的观测信息, 提取其中的相对运动信息，包括导弹对飞机的相对运动速度Δv、导弹转动角速度Δω、无人机与导弹相对运动距离D、无人机所处飞行高度H。

步骤4 将无人机与每一枚敌方空空导弹经过步骤2和步骤3得到的状态信息进行拼接, 然后归一化, 保存为状态单元Si, 如下所示:

(9)

步骤5 无人机在面临多枚导弹打击的情况下, 越早遭遇导弹, 威胁紧急程度越高, 需要优先进行考虑。与自然语言处理一样, 单词出现的先后顺序会呈现出一定的相关性, 状态单元之间也会存在这种联系。采用下式估计无人机与导弹的碰撞时间:

(10)

式中: D为无人机到导弹形成的距离向量, 

为无人机与该导弹速度矢量和在D方向上的投影, 由式(10)可得到遭遇导弹的剩余时间估计量

。

步骤6 按照

对状态单元进行排序并结合, 构成单元状态序列USS，USS =[S0, S1, S2, …, SN]。导弹数量是不固定的, 因此USS中含有的状态单元数量不固定。

2.2  隐藏特征提取

USS能对无人机当前所处的环境信息进行唯一标识, 使用GRU网络对USS中的状态单元进行特征融合, 提取隐藏特征的详细步骤如下。

步骤1 初始化隐藏特征hzero为全零矩阵。

步骤2 将前一时刻隐藏特征

与当前状态单元St输入公式进行计算, 得到更新门神经元向量zt。

(11)

步骤3 将前一时刻隐藏特征

与当前状态单元St输入公式进行计算, 得到重置门神经元向量rt。

(12)

步骤4 将前一时刻隐藏特征ht-1、当前状态单元St以及重置门神经元向量rt输入到公式进行计算, 得到候选隐藏特征

。

(13)

步骤5 将前一时刻隐藏特征ht－1、更新门神经元向量zt以及候选隐藏特征

进行计算, 在平衡历史特征的同时加入了新状态所包含的信息, 求到新的隐藏特征。

(14)

步骤6 如果USS中还有状态单元St+1, 则将新的隐藏特征ht和该状态单元St+1返回步骤2进行计算。

步骤7 得到USS的隐藏特征hN, 将其作为该时刻USS的隐藏特征输出Feature。

其中, Wr、Wz和

都是可学习参数, σ为sigmoid函数, 输出0~1为信息所占百分比。在强化学习动作选择阶段, 直接使用特征输出Feature作为神经网络的输入, 选择动作; 在训练阶段，同样使用GRU提取单元状态序列中的特征Feature, 输入神经网络, 反向传播过程中的神经网络误差值error关于状态单元S的梯度Δe(S)将用于GRU网络中Wr、Wz和

的更新。

2.3  结合DDQN算法构建的算法

环境中的观测信息经过状态编码转码为USS后, 再使用GRU进行特征融合与提取, 就能得到定长编码的特征信息Feature, 可将其直接作为强化学习的神经网络输入。

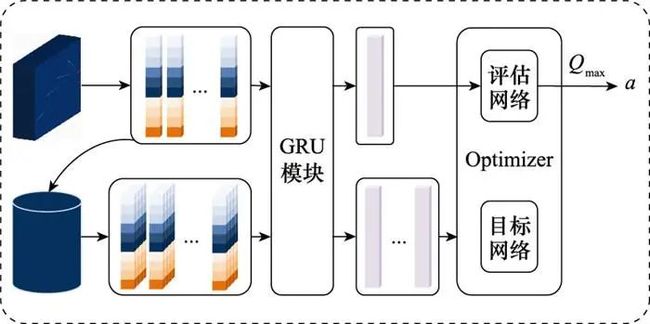
结合DDQN算法, 构建基于DDQN的算法(DDQN algorithm based on USS, SSDDQN), 其算法流程如图 4所示。SSDDQN维护一个GRU模块，用于提取USS中的隐藏特征, 优化器通过式(2)计算评估网络梯度, 然后更新评估网络参数, 梯度参数会传播到GRU模块，以进行同步更新。

图4   SSDDQN算法流程

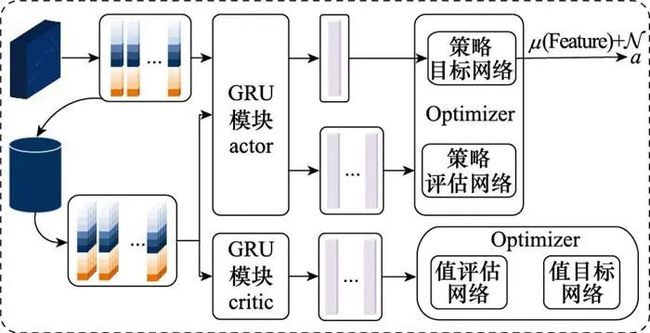
结合DDPG算法, 构建基于USS的DDPG算法(DDPG algorithm based on USS, SSDDPG), 其算法流程如图 5所示。SSDDPG维护两个GRU模块, Feature分别用于策略网络和值网络。值网络优化器通过式(4)计算值神经网络梯度, 策略网络优化器通过式(7)计算策略梯度, 网络参数更新时的梯度参数会传播到对应GRU模块进行更新。

图5   SSDDPG算法流程

3 基于强化学习的空战决策

3.1  无人机机动模型

本文研究的无人机动力学模型如图 6所示, 可将无人机视作左右对称的理想刚体, 其运动方式表示为三自由度飞行控制仿真[37]。将无人机所受的合力沿运动方向和垂直于运动方向进行分解, nv表示升力、阻力和推力的合力对速度产生的影响, 提供切向加速度; 无人机的法向过载用nh表示, 垂直于速度方向, 控制无人机俯仰角; 滚转角用μ表示; 重力加速度用g表示。

图6   无人机动力学模型

无人机三自由度仿真的运动方程如下:

(15)

式中: β为俯仰角, 表示速度与水平面的夹角, 取值范围为[－π/2, π/2], 水平面向上为正, 向下为负; α为方位角, 表示速度在水平面上的投影与正北方向的夹角, 大小范围为[0, 2π]。

3.2  无人机动作空间

本文中的无人机动作以其运动方向和飞行姿态为相对坐标系的原点, 始终保持无人机以最大速度进行飞行, 即切向过载nv=sin β。智能体通过改变无人机的滚转角μ和法向过载nh控制无人机机动。其中，μ∈[－π/2, π/2], nh∈[－Gmax, Gmax]。

DDPG算法直接输出两个-1到1的动作, 并分别按照滚转角μ和法向过载nh进行反归一化, 控制无人机机动。

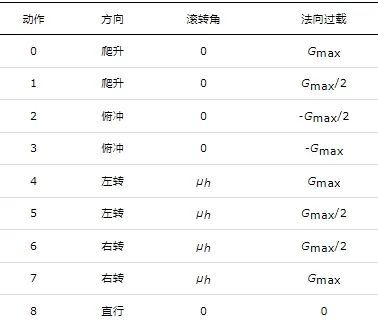
DDQN算法适用于处理离散型的动作决策, 对于无人机智能机动这种连续型的动作空间, 普遍做法是将连续动作进行离散化处理[38], 将其转换为离散机动控制。根据美国国家航空航天局提出的空战基本动作库, 按照机动方向和过载大小，将滚转角与过载离散化为表 1所示的9个基础动作。其中，滚转角μh与当前俯仰角β的关系如下:

表1   DDQN算法的动作空间

(16)

此时，

, 无人机会以当前运动平面做转向机动。

3.3  实验奖励设计

智能体在训练的过程中, 由于任务完成次数太少或任务步数过大, 会导致学习缓慢, 甚至无法收敛。本文通过奖励重塑给智能体设计阶段性目标, 引导智能体朝着完成任务的方向前进。

(1) 高度奖励

无人机最高飞行高度为15 km, 最低飞行高度为2 km, 在规避机动的过程中可能出现越过边界的情况, 超过高度限制则判定为损毁。考虑到靠近边界则处于危险态势, 为减少在规避过程中超过边界导致损毁的现象, 建立高度奖励函数:

（17）

(2) 规避奖励

在多枚导弹打击无人机时, 将任务拆分为规避多个单枚导弹的阶段性任务, 并鼓励智能体规避更多导弹。奖励出现在导弹爆炸时, 设计成功规避奖励:

(18)

(3) 仿真结束奖励

在连续规避空空导弹的问题中, 最终的决策评价标准为无人机能否生存。在一局仿真模拟结束时, 根据无人机生存状态，建立生存奖励:

(19)

针对战斗机规避导弹问题, 考虑以上3种奖励, 建立环境奖励函数:

 (20)

4 超视距空战仿真实验

本文实验平台采用由中国指挥与控制学会和共青团航空工业集团委员会联合主办的“2021首届全国空中智能博弈大赛”的决赛环境。该平台以作战计划和方案为研究对象, 构建典型空战场景, 拓展空战作战样式和作战机理, 赋能作战指挥决策。

4.1  规避导弹任务想定

针对无人机规避空空导弹问题, 实验设计了两个任务想定: ①蓝方飞机挂载导弹随机出现在红方无人机四周, 并利用导弹进行打击, 红方无人机通过连续机动决策规避导弹; ②蓝方4架飞机分别挂载导弹, 同时从不同方向攻击无人机。红方无人机尝试通过连续机动决策以求规避全部导弹, 并最终获得生存。

影响空空导弹对无人机进行有效打击的因素有很多, 包括导弹和无人机的速度、高度、俯仰角、朝向角、目标进入角以及导弹制导律、无人机机动方式等。为衡量在不同态势下智能体控制无人机规避导弹的性能优劣, 设计如图 7所示的初始场景。红方无人机速度为400 m/s, 最大过载Gmax为6g, 初始高度为9 km。蓝方无人机携带空空导弹在距离红方无人机20 km到60 km、高度在3 km到15 km的范围随机出现。蓝方飞机在导弹发射之后便跟随红方无人机飞行, 为导弹制导提供雷达照射。

图7   初始想定场景

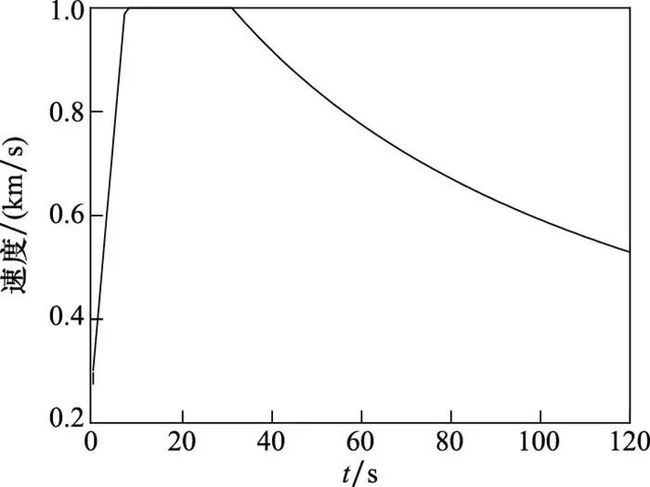
空空导弹的初始速度为300 m/s, 最大速度为1 000 m/s, 发动机工作时间为30 s, 其速度变化如图 8所示。导弹在发射之后会先急剧加速, 在到达最大速度后匀速飞行, 发动机停止工作后做减速运动。导弹制导规则为比例导引算法, 杀伤半径为100 m, 脱靶后会立即爆炸。

图8   导弹飞行速度随时间变化的曲线

4.2  神经网络参数

在强化学习中，DDQN算法、DDPG算法、SSDDQN算法以及SSDDPG算法的神经网络均采用3层反向传播神经网络, 每一层神经元节点个数分别为256, 256, 256, 经验池大小为50 000。DDQN算法和DDPG算法的输入将状态单元Si按最大实体数目进行直接拼接, 初始状态默认为0, 对存在的实体按状态值进行填充, 即在单枚导弹场景训练时的输入维度为10, 在4枚导弹场景训练时的输入维度为40。SSDDQN算法和SSDDPG算法均使用GRU网络单元进行特征提取, GRU网络单元以USS为输入, 输出维度为10的隐藏特征Feature, 隐藏特征用于强化学习训练和动作选择。

在DDQN算法和SSDDQN算法中, 折扣系数γ= 0.99, 学习率lr=1e－4, 网络更新频率为100, 即训练100次，就能将评估网络的参数拷贝到目标网络中。在DDPG算法和SSDDPG算法中, 折扣系数γ=0.99, 值网络学习率lrc=5e－4, 策略网络学习率lra=1e－4, 软更新频率τ=0.01。每训练2 000局, 就利用训练后的智能体完成1 000轮对局测试，以记录规避导弹存活率。

4.3 仿真实验分析

在实验中, DDQN算法、DDPG算法、SSDDQN算法以及SSDDPG算法分别在想定①和想定②的场景中进行训练, 并将4种强化学习算法与3种简单的固定机动策略进行比较，即高速直线飞行、高速俯冲、最大过载转圈。本文分析了规避导弹的存活率、智能体控制无人机连续规避导弹的飞行轨迹，以及不同机动方式下的导弹脱靶量。

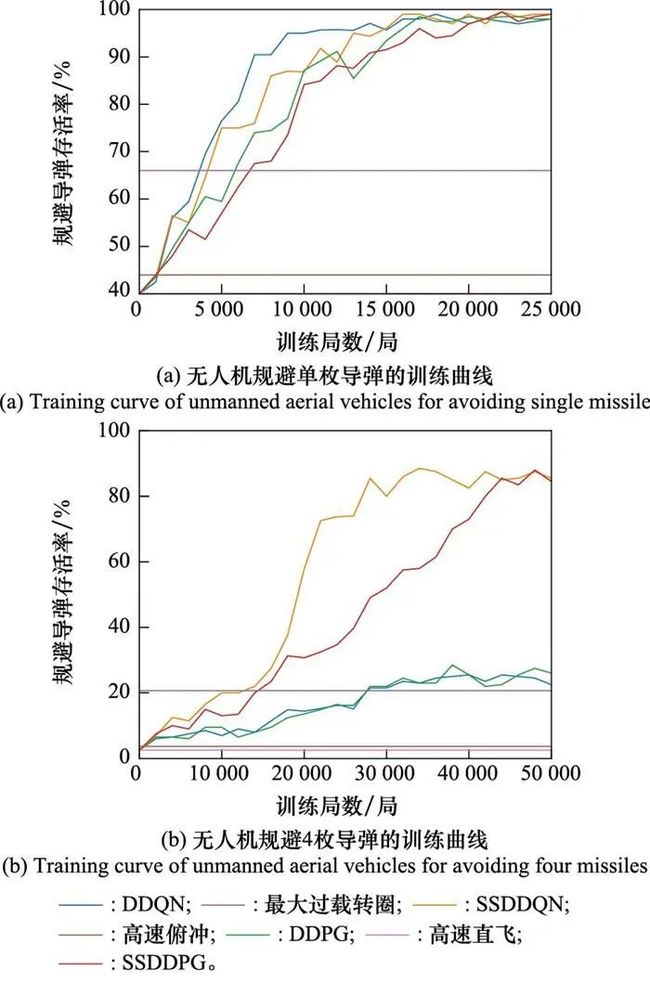
 4.3.1   规避导弹成功率

在想定①中的训练曲线如图 9(a)所示: 高速直线飞行、高速俯冲、最大过载转圈面对导弹打击时的存活率分别为40%、44%、67%;DDQN、DDPG、SSDDQN、SSDDPG这4种算法面对导弹打击时的最高存活率分别为99%、99.5%、98.5%、99.5%。在3种简单机动算法中, 只有最大过载转圈机动策略的存活率超过了60%, 而由4种强化学习算法训练出来的智能体操纵无人机规避导弹的存活率均超过了98%, 证明强化学习能够在无人机规避导弹场景下训练出具有自主机动决策的智能体。同时发现, 增加了USS的强化学习算法在收敛速度上比传统强化学习算法更慢, 但最终的智能体规避导弹的存活率差异很小。在想定②中的训练曲线如图 9(b)所示: 高速直线飞行、高速俯冲、最大过载转圈在导弹打击时的存活率分别为2.5%、3.7%、20.1%;DDQN、DDPG、SSDDQN、SSDDPG这4种算法在导弹打击时的最高存活率分别为25.5%、28.5%、88.5%、88%。增加打击无人机的导弹数量后, 高速直线飞行和高速俯冲机动这两种机动方式很难存活, 最大过载转圈这种机动方式仍然具有一定的规避能力。DDQN算法和DDPG算法在该场景下虽然也能够提升连续规避多枚导弹的存活率, 但是其收敛效果较差。结合USS的SSDDQN算法与SSDDPG算法, 在应对4枚导弹时仍然能够训练出以很大概率规避全部导弹的智能体。对比发现, 结合USS的强化学习算法在多枚导弹同时打击场景下的收敛速度更快、精度更高, 能够明显提升无人机连续规避多枚空空导弹打击的存活率。

图9   无人机规避导弹打击的训练曲线

由图 9可知, 由SSRL算法训练的智能体在规避单枚空空导弹中的存活率与DDQN算法和DDPG算法相当, 并且在连续规避多枚空空导弹中的存活率远高于DDQN算法和DDPG算法。

4.3.2  无人机规避飞行轨迹

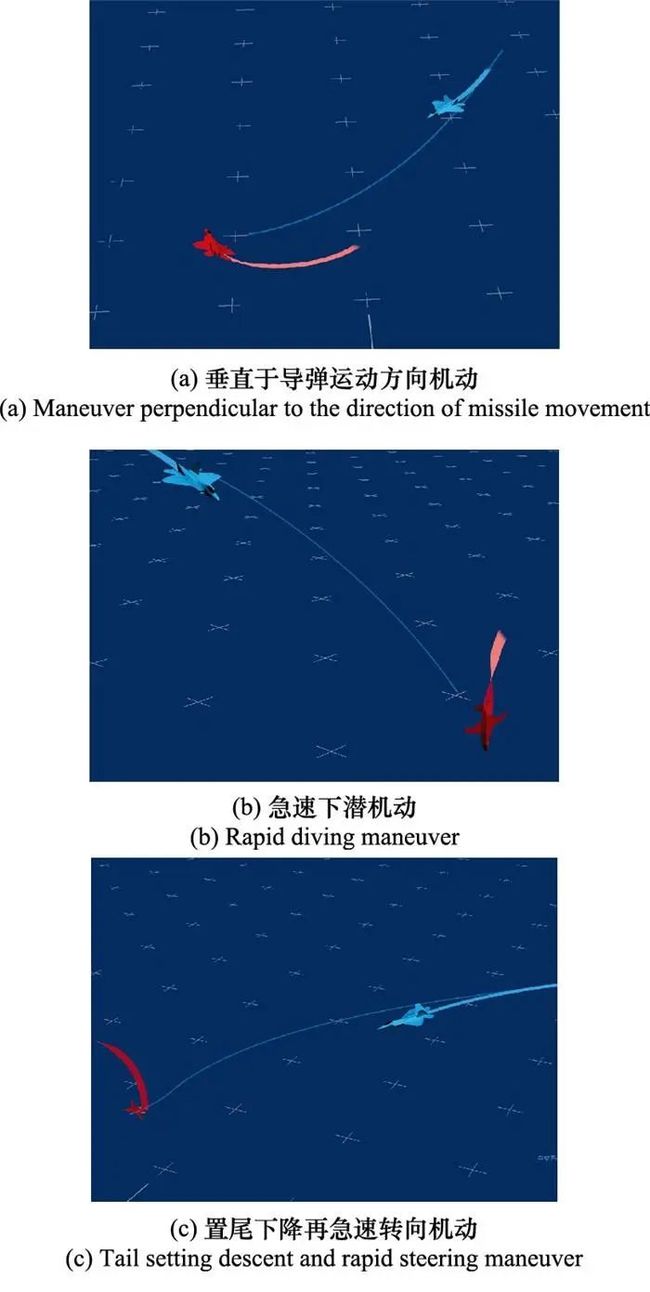
在想定①中, DDQN算法、DDPG算法、SSDDQN算法、SSDDPG算法训练的智能体, 针对不同态势来袭的导弹会采取不同的规避机动方式。训练出的典型机动方式如图 10所示, 包括垂直于导弹运动方向、急速下潜、垂直置尾再急速转向等机动方式。智能体根据态势不同和飞行速度不同的来袭导弹，会选择采用不同的机动方式进行规避, 尽管这些机动方式不同, 但是都能够有效规避智能体遭遇导弹的攻击。

图10   无人机规避单枚导弹的飞行轨迹

在想定②中, SSDDQN算法与SSDDPG算法训练的智能体控制无人机机动的飞行轨迹近似, 如图 11所示。图 11(a)为SSRL算法训练的智能体控制无人机连续规避4枚导弹的飞行轨迹。在规避导弹的整个过程中, 智能体采取不规则的爬升和俯冲动作, 并在最后时刻使用最大过载进行极限转向。图 11(b)为无人机遭遇导弹阶段的飞行轨迹, 当导弹靠近时, 智能体控制无人机在垂直平面做不规则的蛇形机动, 不断调整飞行姿态, 使得无人机在最后时刻能够通过反向大机动规避空空导弹。

图11   无人机规避4枚导弹的飞行轨迹

4.3.3   导弹脱靶量

脱靶量是用来形容导弹与目标在运动过程中相对距离的最小值, 是评定导弹系统命中精度的重要指标, 脱靶量的大小能够直接影响导弹的毁伤概率。脱靶量越大, 导弹对无人机的威胁度越低, 当导弹的脱靶量大于攻击范围时, 无人机可以成功避开导弹。在遭遇阶段, 可以认为导弹和无人机均做匀速直线运动, 并以此计算智能体应对不同位置来袭导弹的平均脱靶量。

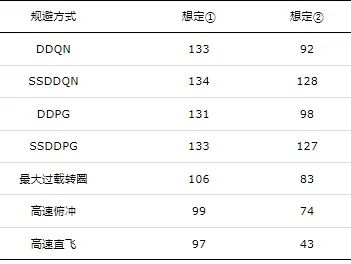
图 12为不同机动方式下的导弹脱靶量箱型分布, 表 2为不同机动方式下的导弹平均脱靶量。图 12 (a)为想定①中导弹对无人机脱靶量的箱型分布: 高速直线飞行、高速俯冲的平均脱靶量集中在100 m范围内, 平均脱靶量分别为97 m、99 m; 最大过载转圈的脱靶量集中在100 m周围, 平均导弹脱靶量为106 m; DDQN算法、SSDDQN算法、DDPG算法、SSDDPG算法训练的智能体应对导弹的脱靶量集中在132 m周围。图 12 (b)为想定②中导弹对无人机脱靶量的箱型分布: 高速直线飞行、高速俯冲、最大过载转圈的脱靶量集中在100 m范围内, 平均脱靶量分别为43 m、74 m、83 m; DDQN算法、DDPG算法训练的智能体应对导弹的脱靶量分别为92 m、98 m; SSDDQN算法、SSDDPG算法训练的智能体应对导弹的脱靶量分别为128 m、127 m。由此可知, 在连续规避导弹的场景中, SSRL算法训练的智能体能够有效提高导弹脱靶量, 更好地避开导弹的打击。

图12   不同机动方式下的导弹脱靶量

表2   导弹平均脱靶量

5 结论

本文针对超视距空战中无人机在面对多枚导弹同时打击情景下状态空间维度大、状态信息维度不断变化、强化学习算法训练效果差等问题, 提出使用USS表示单实体对多目标场景下的状态特征, 并利用GRU网络对USS进行特征融合与提取, 提取的特征用于强化学习, 构成SSRL算法。算法在“2021首届全国空中智能博弈大赛”仿真平台上进行训练。仿真结果表明, 相比DDQN算法、DDPG算法、简单机动算法, SSRL算法训练出来的智能体能够增加导弹脱靶量, 提升无人机在连续规避导弹场景中的存活率。

声明:公众号转载的文章及图片出于非商业性的教育和科研目的供大家参考和探讨，并不意味着支持其观点或证实其内容的真实性。版权归原作者所有，如转载稿涉及版权等问题，请立即联系我们删除

“人工智能技术与咨询”   发布