ZK-Rollups工作原理
1. 引言
ZK-Rollups是借助零知识证明技术来对以太坊进行扩容。
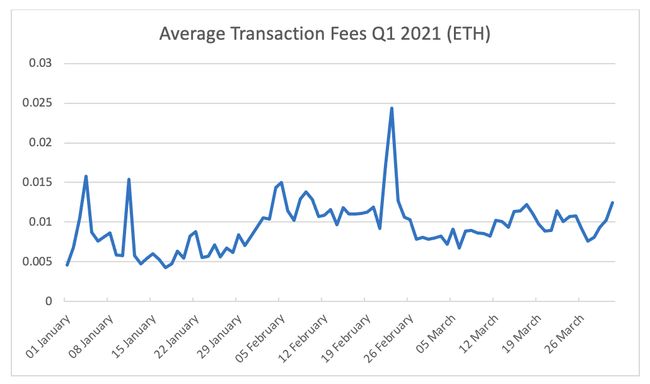
对于公开账本来说,扩容是老生常谈的问题。随着过去一年来公开账本上活动的增加,该问题的紧迫性加强了,具体体现在交易费用上——以太坊上常规合约交互的交易费在$40左右。
主要有2种方式来解决该问题:
- 1)在基础层(即Layer 1)扩容,借助分片和新型共识协议。
- 2)在Layer2扩容
2. Layer 2(L2)
除基础层扩容之外,layer 2扩容技术仍有一席之地,原因有:
- 隐私
- 高性能、特定应用网络(可利用现有公共账本的安全性和流动性)
当前,采用L2协议的主要原因是扩容性。L2协议可以高效方式对现有公共账本进行扩容,并为以太坊等智能合约平台提供近中期解决方案。
现有的L2扩容技术主要有:
- 1)Channels:通道。需要在链上锁定资金、需要实时监测链上状态防止对方作弊。
- 2)Plasma:需要信任operator,并存在大规模退出问题。
- 3)Rollups:取决于state transitions在链上验证方式的不同,可分为:
- 3.1)Optimistic Rollups:通过欺诈证明来验证state transition。
- 3.2)ZK-Rollups:通过zero-knowledge-proofs来验证state transition。
2.1 通道 L2扩容技术
通道是在2方之间建立,允许相互瞬时来回转账。这些pair-wise,双向通道可借助P2P gossip协议和probabilistic network routing技术,构成通道网络。类似有Bitcoin的闪电网络。
不受限于转账,可构建支持smart contract state transition的状态通道。
但是,通道的开销在于:
- 1)需要初始funding交易,为该通道锁定资金。对于单一通道来说还好,但是当需要通过网络进行路由转账时,复杂度会更高,路由时中间通道的流动性锁定使得其“资金效率不高”。
- 2)通道的双方需要监测L1基础层,以确保对方遵守协议。
通道适于的用户场景为:
- 双向支付,使得服务提供商的客户在消费时借助通道进行支付。
- 当双方有长期、大量资金往来(状态更新)时。
2.2 Plasma
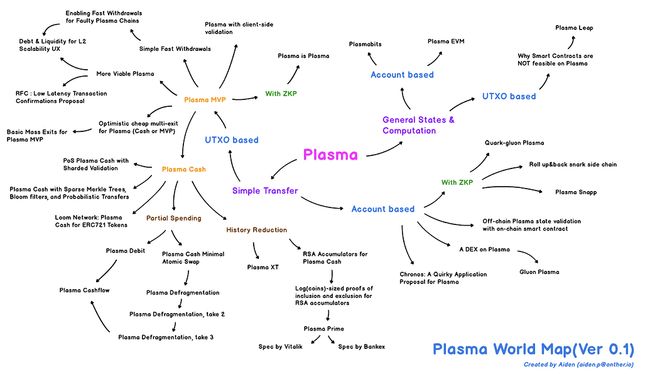
上图摘自Plasma World Map - the hitchhiker’s guide to the plasma。
不同的Plasma方案各有侧重,但是用户体验都较差:
- Plasma Cash:代币必须有固定的、不可分割的面额。用户存入的每个token都需要保留大量的数据。
- Plasma MVP:包含了复杂的理论来保证withdrawals的安全性,每笔withdrawal交易包含多个签名。
- Plasma Debit:用户必须存储very large sized proofs,同时operator需要锁定大量的资金,以创建pre-emptive(先发制人的)通道。
所有的Plasma都假设存入的资产具有明确的owner,从而实际上阻止了创建更复杂的应用程序——如AMM自动做市商或EVM。
此外,Plasma侧链中,若某operator出了问题,无法保证其它operator可接管该Plasma chain。
Plasma要求信任operator,同时存在“mass-exit”大规模退出问题(确实发生了)——即Plasma chain上的大量用户同时赎回,在L1层造成巨大的拥塞和高交易费用,导致许多人不可避免地不得不等待相当长的一段时间才能获得资金。
2.3 Rollups
Rollups可称为“混合”layer 2,其将计算移到链下,而将数据保存在链上——这是与Plasma的最大不同之处,也是解决数据可用性的关键。
与Plasma类似,Rollups包含了提交a state commitment 或 “state root” 到Layer 1 EVM上的某智能合约。该state root派生自rollup中的所有deposits/accounts的state,采用某种密码学累加器(通常为merkle tree)。当state root更新时,新的state root提交时会伴随有a batch of all the transactions for that update。
这就意味着,任何人都可获取数据——为一系列state deltas,重构出rollup的state,然后创建新的batches。
这为rollup的用户提供了安全性,可降低单个operator交易对手的风险,以及多个operator共谋的风险。在rollup中负责打包交易并提交上链的coordinator,可能会神奇消失,而其他人很容易接替其剩下的工作。
有些rollups设计要求多个coordinators。如,有的rollup要求对提交的每个batch进行拍卖,任何人都可出价称为coordinator,若竞价成功,可获得创建a batch of transactions的权利,并从该batch中赚取交易手续费。
2.3.1 Optimistic Rollups
optimistic rollups某种程度上可称为“荣誉系统”——L1智能合约不会检查state transitions是否运行正确。当coordinator提交新的state root时,合约仅是简单采纳coordinator所述,接受该state update。
当且仅当某人向合约提交“fraud proof”(欺诈证明)时,合约才会检查该state transition,对fraud proof进行验证,具体包含:
- a proof of “pre-state”,即某交易提交之前的状态。
- a proof of “post-state”,即某交易提交之后,operator所声称的状态。
- a proof of the transaction that was applied during a state transition。
rollup会验证以上proofs,以验证:
the pre-state, post-state and transaction were all included as part of a state transition submitted by a coordinator。
然后合约会对pre-state应用该transaction logic,将结果与post state进行比较。若不匹配,则证明coordinator未正确应用该交易,此时合约会回滚该state transition及其后续状态,回滚到the last known valid state。同时,合约会slash 该coordinator的质押,惩罚coordinator的欺诈或错误行为。
事实证明,这种方法非常强大。事实上,它允许构建一些相当复杂的rollup构造,以至于我们可以在optimistic rollup中构建整个第2层EVM。这意味着L1 EVM可以移植到L2,并且仍然或多或少完全相同。
这种方法唯一真正的权衡是需要对提款进行时间锁定,以允许挑战期。这可能会使大规模rollups变得“资金效率低下”,通常意味着需引入流动性提供者以加快提款。
3. ZK-Rollups及其工作原理
ZK-Rollups由Barry Whitehat在2018年底2019年初首次提出:
- https://github.com/barryWhiteHat/roll_up_token
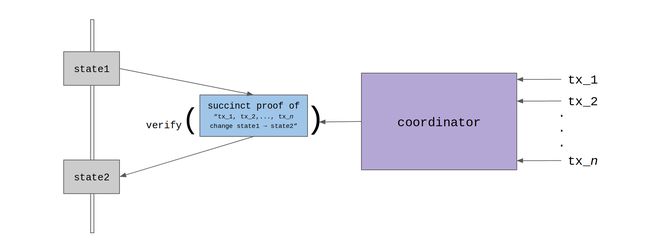
实际有多种ZK-Rollups实现。本文重点解释基于Barry Whitehat原始设计的basic principles。
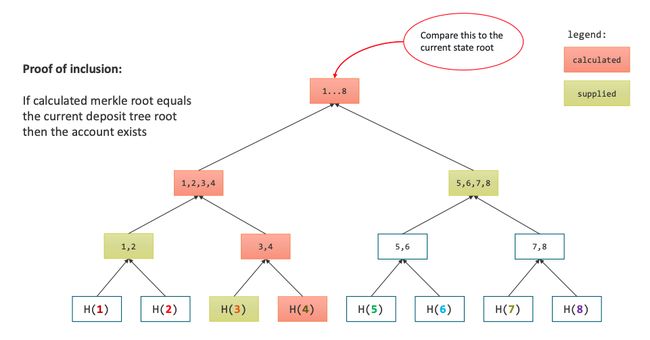
与Optimistic rollups类似,ZK-rollups在Merkle tree中存储所有的addresses和相应的balances。该“balance tree”的root会存储在链上智能合约。

当向链上提交a batch时,会提议新的merkle root(以反映更新后的merkle tree),同时也在该batch中包含了updated balances from all the transfers。伴随batch提交的还有一个snark proof,合约会验证该proof,若通过则接受新的merkle root,使其成为合约的canonical state root。
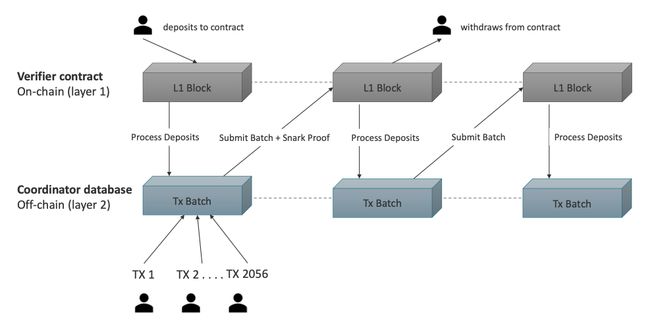
一个简单的rollup主要包含3类主要的活动:
- 1)存款
- 2)转账
- 3)取款
3.1 ZK-Rollups存款

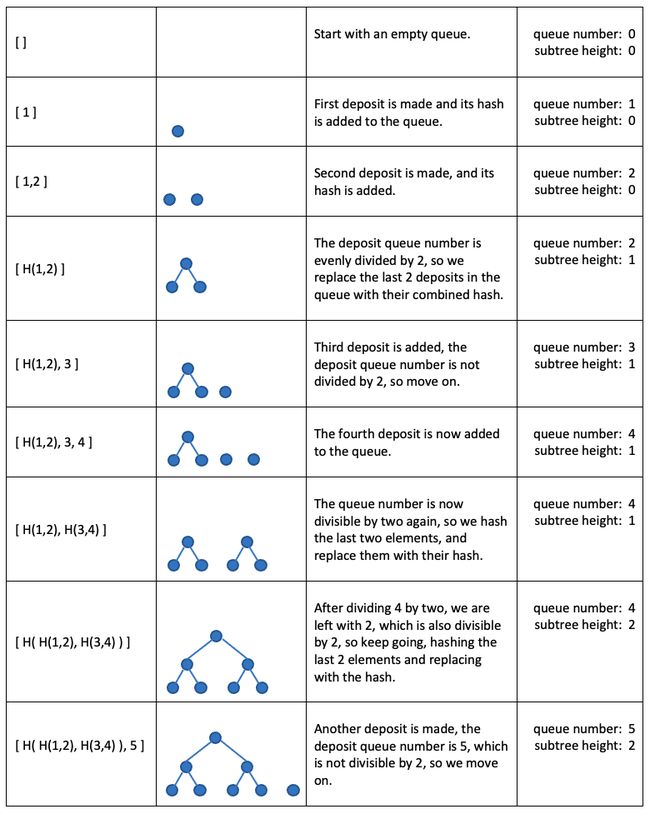
存款是指:向rollup合约发送tokens。rollup合约会将这些tokens添加到a pending deposit queue。某个时刻,coordinator会取一定数量的deposits,将其添加到rollup,这包含了将其包含在merkle tree of balances中。添加到balance tree的方法有a clever trick,借助名为merkle mountain ranges的技术。
向rollup合约存款,此时deposit queue中有1个deposit:
Hash(pubkey, amount, token type) = 0x1234abcd…
再存入一笔:
Hash(pubkey, amount, token type) = 0x9876fedc…
此时deposit queue为:
[0x1234abcd, 0x9876fedc]
此时有偶数个deposits,会对queue中的最后2个进行哈希:
Hash([0x1234abcd, 0x9876fedc]) = 0x6663333
此时deposit queue为:
[0x6663333]
该单一哈希值表示了向合约存入的2笔deposits,但是,coordinator如何知道该哈希值代表的具体内容呢?我们如何得知该哈希值是对应一笔deposit,还是2笔,甚至是16笔?
有2种方式来解决该问题:
- 1)每笔deposit会释放一个event,coordinator可订阅该事件,从而可跟踪每笔deposit的详细内容。
- 2)合约会维护pending deposit queue的size count 以及 pending deposits sub tree height。
接下来,需要考虑的是,如何将queue中的deposits移到rollup呢?
rollup中所有的deposits和balances都是存储在a sparse merkle tree中的。该merkle tree具有fixed size,预初始化为all zeros(或相应的哈希值)。
为了处理pending deposits,coordinator会从pending deposits queue中取第一个元素,然后插入到rollup的sparse balance tree中的合适高度,这将导致新的merkle root for the balance tree, which the coordinator posts to the rollup contract。
为accept该new balance tree merkle root,必须确保coordinator将该deposit subtree插入balance tree的previously empty part。为此,coordinator需提交a merkle proof of an empty node at the corresponding level of the balance tree,然后将其替换为the root of the deposit subtree,类似为:
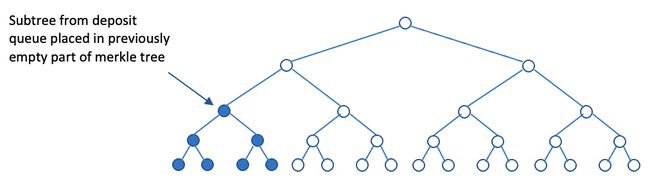
至此,合约已拥有验证deposit subtree正确并入到rollup中所需的一切信息,如:
- 知道sub tree height,本例中为2。
- 知道what an empty node at a height of 2 is,因为其有a cache of empty node hashes for each level of the tree。
- 已给了a merkle proof for this empty node,使得其可验证it is part of the current balance tree。
- 具有the root of the deposit tree(为deposit quque的第一个元素)。
合约可简单地从node hashes cache中取出empty node hash值,然后用该值和给定的merkle proof来验证当前balance tree root。若验证通过,则从deposit queue中取第一个值,与supplied merkle proof一起,派生出新的balance tree root,若派生出的新balance tree root与coordinator提交的一致,则合约accept。
此时,coordinator可向任意存款人提供merkle proof,使其可独立验证其存款是否已处理入rollup。
若你观察得足够仔细,可发现,当coordinator处理pending deposits for the queue时,其仅处理4个deposits到rollup内,剩余1个不处理。这是因为coordinator仅可take the “perfect tallest subtree” at any given time,该值必须为a power of 2。剩下的deposits将后续处理。
3.2 ZK-Rollups转账 以及 zero-knowledge proof
一旦存款成功,可将其资金在rollup账号间快速、便宜地转账。具体为,向coordinator发送a transfer transaction,然后coordinator将其与其他交易打包并提交到rollup合约,会同时提交an updated balance tree root以及a zero-knowledge proof。
可根据batch中的交易来派生出updated balance tree root。If Alice submits a transaction to say “send 10 tokens to Bob”, the coordinator will increase Bob’s balance by 10, reduce Alice’s balance by 10, re-hash the account data to get new account leaves, and rebuild the merkle tree. This results in a new merkle root, which gets sent to the smart contract.
不过不同于Optimistic rollups,ZK-Rollups中,智能合约并不会直接采纳coordinator所述,ZK-Rollups为trustless的,无需信任任何coordinator。coordinator需为batch内的所有交易创建a proof。
通过订阅智能合约释放的deposit events,每个coordinator都维护了a local database of deposits。当收到一笔交易时,coordinator会根据其数据库做如下验证:
- 该交易是正确的,并对应付款人的公钥。
- 付款人的账号存在于balance tree中。
- 转账的金额未超过付款人的余额。
- 收款人账号存在于balance tree中。
- 付款人和收款人具有相同的token type。
- 付款人的nonce值正确。
- 不存在overflow或underflow情况。
一旦验证通过,该交易会被添加到quque中。一旦queue内有一定数量的交易,coordinator将创建a batch。为此,coordinator需编译a bunch of inputs for the zk-proof circuit to compile into a proof,具体包含:
- 为batch内的所有交易创建a merkle tree,可填充dummy transactions以满足circuit的size要求,然后为每笔交易创建a merkle proof。
- 为所有交易的每个收款人和付款人创建一组merkle proof,以证明收款人账号的存在性和付款人账号的存在性。
- 每笔交易更新付款人和收款人账号 引起的对balance tree root的更新,基于此创建派生出的一组中间root值。【可向合约证明batch 内的交易都applied correctly。】
该circuit具有3个public signals:
- pre-state root
- post-state root
- transaction root
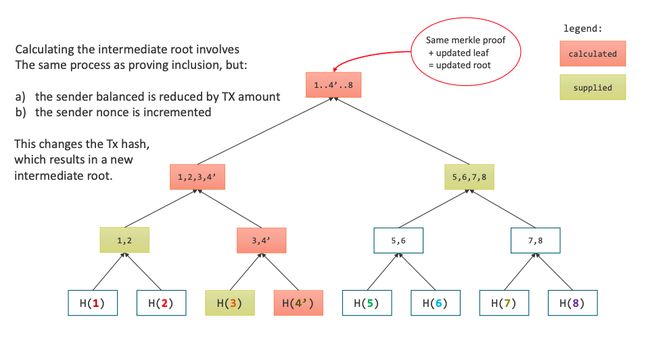
该circuit通过遍历所有交易创建a proof,执行与coordinator相同的检查和验证。每次迭代,circuit会:
- 首先借助账号merkle proof 检查付款方存在于当前root下。
- 减少付款人的余额,增加其nonce,对updated account data重新哈希,然后利用该新哈希值与账号的merkle proof一起,派生出新的merkle root。
至此,可知,该merkle root反应了 “balance tree中仅修改了付款方的余额和nonce值” 的实时。为何呢?因为我们采用 证明该账号在当前balance tree root下的同一merkle proof来派生的new balance root。
与上面类似,针对收款方账号,circuit会:
- 借助所提供的merkle proof,验证收款方账号在new intermediate root下存在。
- 增加收款方的余额
- 对收款方账号重新哈希,使用相同的merkle proof来计算新的balance tree root。
对每笔交易重复以上流程。每次迭代,更新付款方账号都会更新state root,更新收款方账号也会再次更新state root。
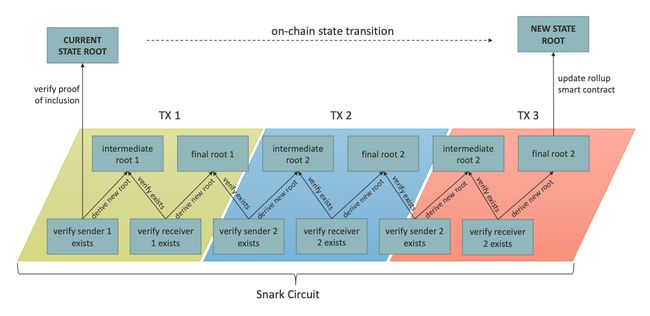
每个updated state root一次仅反应一件事,这样,circuit遍历batch内的所有交易,创建a chain of updates,在最后一笔交易处理完时,会生成a final balance tree root。该final root将称为rollup的新state root。
3.3 L1 Finality 以及 ZK-Rollups取款
一旦circuit为所有state updates完成了zero-knowledge proof创建,coordinator会将该proof提交到智能合约,circuit会验证该proof,并验证该proof中的3个public signals:
- the pre-state root,即,the balance tree root as it is currently is before the batch is accepted。
- the post-state root,即,the final root after applying all the state updates in the circuit。
- the transaction tree root。
若合约中的pre-state root与记录在合约内的当前balance tree匹配,且proof有效,则合约会从proof中提取post-state root,更新当前balance tree以与其匹配。
此时,任何存款人都可向合约请求验证器余额——对其account进行哈希,将该哈希值提交给合约,同时提交a merkle proof来验证当前account tree root。
若存款人想要从L1取款?
proof中的3个public signals之一为transaction root,该root对应的merkle tree中包含了输入到circuit内的所有交易。每笔交易都关联一个merkle proof可验证该transaction root。当向合约提交a batch时,合约会记录该transaction root,使得任何存款人都可验证其交易包含在该batch内,然后向智能合约提供该transaction details、a merkle proof以及transaction root。智能合约会:
- 对transaction data进行哈希
- 验证相应的transaction root在合约中有记录
- transaction hash与transaction root对应所提供的merkle proof可验证通过
为了取款,depositor向balance tree中index 0的账号发送资金。该index的账号保留为该用途,将资金发送到该账号并燃烧L2的资金。一旦该交易(向index 0 账号转账的交易)被包含在batch中,depositor可向智能合约发送区块申请,采用以上机制,提交proof of their transaction to the “burn account”。
取款申请中包含了:
- the transaction details
- merkle proof
- transaction tree root
- an L1 address to transfer the tokens to
一旦交易存在性验证通过,智能合约将检查区块是否已处理,然后向L1的特定收款方发送资金。
4. Atomic Swaps
可将Atomic Swaps称为“dependent transactions”。
ZK-Rollups支持向L2 rollup存款,向L2的其他账号转账,以及提款到L1。但是,该功能有限,仅是一个支付网络。
若引入dependent transactions,在此基础之上,可构建一些有趣的事情,如,构建订单簿交易所,匹配订单,然后将每个互惠交易对作为相互依存的交易对。
This is as simple as including the transaction hash of the counterparty transaction in the transaction in each reciprocal pair. (Obviously the counterparty transaction hash cannot be part of the hash itself, or this will create a circular dependency, but there are ways of getting around this).
5. 数据可用性
rollups与plasma的本质区别在于,rollups为混合L2协议。即将计算从L1中移除,而将数据仍保留在L1中。这就意味着,一旦数据提交到L1,任何人都可以重建该rollup然后接收交易和创建batches等待。
为了使使用L1作为数据可用性层成为可能,交易被压缩并作为calldata发布到智能合约。这节省了大量空间,每字节16 gas,节省空间意味着节省gas。从而实现高交易吞吐量。
根据Solidity文档可知:
“Calldata is a non-modifiable, non-persistent area where function arguments are stored, and behaves mostly like memory.”
使用calldata的原因在于其是最便宜的可用存储形式。以calldata参数传输的state-deltas并不会存在在以太坊state中,但是以太坊节点会在区块创建时存储该transaction data。
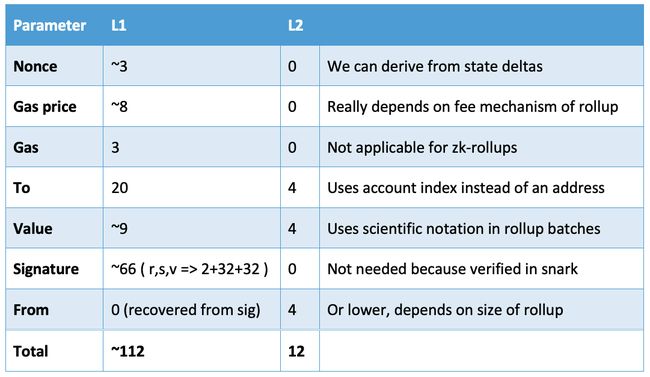
这些state deltas看起来像什么么呢?通过数据压缩节约了多少gas呢?具体为:

6. benchmarking
节约链上数据存储空间 如何 对应为 更高的交易吞吐量?——具体取决于以太坊的block gas limit。
单个区块内能处理的gas量有上限值,由区块内的所有交易共享。
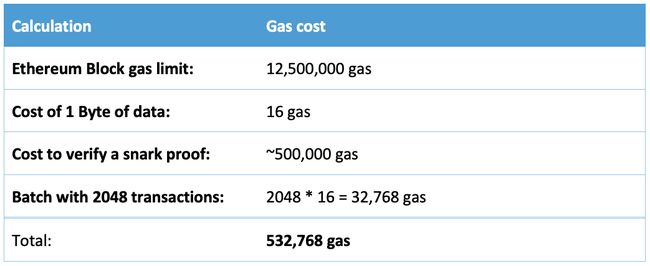
以每个zk-rollup区块内平均包含2048笔交易为例,可发现一个以太坊区块内可最多包含23个batches。(125000000/532768=23,这是一个理论batches数上限值)
相应的tps为:
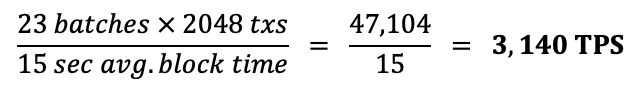
若以太坊区块内一半的交易为Layer 2 rollup,则可达到1500TPS。
之所以一个zk-rollup内约有2000笔交易的原因在于,创建zero-knowledge proof是computationally expensive的,受限于当前ZKP技术。
希望未来有更多的研究:
- how expensive it is to create a proof? 【以太坊已通过EIP-1108以及EIP-2028对gas费进行了优化。】
- benchmark that maps metrics such as number of transactions per batch, number of accounts in rollup, and how long it takes to create a proof given a certain amount of processing power and memory.
- 区分不同proving system的性能,如groth16, plonk, stark等等。
7. 互操作性
所谓互操作性,是指cross-L2交易,无需通过L1层进行取款-存款操作,也称为mass migrations。
这通常包含batch transfers to another rollup。
8. 小结
当前zk-rolluo的一个缺陷在于L2层缺少智能合约支持,不过目前已有相应开发。
还有一个问题是,运行coordinator node的难度,从而会影响去中心化。如,是否需要昂贵的硬件来生成proofs?
参考资料
[1] Simon Brown 2021年7月博客 How Zk-Rollups Work