数据结构:三元组的构建、相加和快速转置
目录
1.三元组表的定义
2.三元组表的数据结构
3.三元组表的构建
4.输出三元组表
5.两个三元组表相加
代码的流程图
实现代码
6.三元组表的快速转置
算法思想
代码实现
7.三元组表输出矩阵
8.全部代码
9.总结
1.三元组表的定义
三元组研究目的 对于在实际问题中出现的大型的稀疏矩阵,若用常规分配方法在计算机中储存,将会产生大量的内存浪费,而且在访问和操作的时候也会造成大量时间上的浪费,为了解决这一问题,从而产生了多种解决方案。 由于其自身的稀疏特性,通过压缩可以大大节省稀疏矩阵的内存代价。
主要是用来存储 稀疏矩阵 的一种压缩方式,也叫三元组表。 假设以顺序 存储结构 来表示三元组表(triple table),则得到 稀疏矩阵 的一种压缩存储方式,即三元组顺序表,简称三元组表。
2.三元组表的数据结构
#define MAX 1000
typedef struct
{
int row,col,e; //数据所在的行、列,数值
}Triple;
typedef struct
{
Triple data[MAX+1];
int mu,nu,tu; //矩阵的行数,列数和非零元个数
}TSMatrix;3.三元组表的构建
思路:从第一行开始遍历查找非零元素,存入三元组表data[tu]中,data[tu].row=i,data[tu].col=j,data[tu].e=a[i][j]
void input(TSMatrix *p,int m,int n)
{
int i,j;
int a[100][100];
for( i=1;i<=m;i++) //随机生成稀疏矩阵
for(j=1;j<=n;j++)
{
if(1+rand()%4>=1+rand()%19)
a[i][j]=1+rand()%99;
else
a[i][j]=0;
}
for(int i=1;i<=m;i++){ //打印出该稀疏矩阵
for(int j=1;j<=n;j++)
{
printf("%4d",a[i][j]);
}printf("\n");
}
p->tu=0; //三元组表的总个数
for(i=1;i<=m;i++) //进行查找非零元素进行存储
for(j=1;j<=n;j++)
{
if(a[i][j]!=0)
{
p->data[p->tu].row=i; //行
p->data[p->tu].col=j; //列
p->data[p->tu].e=a[i][j]; // 数据
++p->tu;
}
}
}4.输出三元组表
void printTriple(TSMatrix *p)
{
printf("\n三元组:\n");
for(int i=0;itu;i++)
{
printf("%4d %4d %4d\n",p->data[i].row,p->data[i].col,p->data[i].e);
}
} 5.两个三元组表相加
思路:两个三元组分别标记两个遍历用的i,j,每次都比较i和j所在位置的row、col值;先比较row的大小,如果i的row小于j的,那就先填i的,然后i++填下一个;如果i和j的row都相同,就去比col,然后i的col小于j,者填i,否则填j的。
如果A与B的row和col都相同,就把row和col分别相加,再存入C中
如果i遍历完,j没遍历完,把j剩余的全放入新的三元组表中;如果i没遍历完,j遍历完,把i剩余的全放入新的三元组表中。
通俗的解释:这个就类似于小编之前的写的顺序表和合并的思路。大家也可以回顾一下两个顺序表的合并思路,联系起来。数据结构:两个顺序表合并算法_业余小程序猿的博客-CSDN博客
注意:只有两个相同行列的矩阵才能相加,所以相加之前要先判断一下能不能。
代码的流程图
实现代码
void sum(TSMatrix *A,TSMatrix *B,TSMatrix *C)
{
C->mu=A->mu; //只有两个行列相同的矩阵才能相加
C->nu=A->nu; //所以用A或B都一样
C->tu=0;
if(A->mu!=B->mu&&A->nu!=B->nu){
printf("矩阵要大小相同才能相加!");
return ;
}
int i=0,j=0;
while(itu&&jtu)
{
if(A->data[i].rowdata[j].row) //A的rowdata[C->tu].row=A->data[i].row; //行
C->data[C->tu].col=A->data[i].col; //列
C->data[C->tu].e=A->data[i].e; // 数据
C->tu++;
i++;
}
else if(A->data[i].row==B->data[j].row) //A的row=B的,再继续比较col
{
if(A->data[i].coldata[j].col) //A的coldata[C->tu].row=A->data[i].row; //行
C->data[C->tu].col=A->data[i].col; //列
C->data[C->tu].e=A->data[i].e; // 数据
C->tu++;
i++;
}
else if(A->data[i].col>B->data[j].col) //A的col>B的,C中加入B的
{
C->data[C->tu].row=B->data[j].row; //行
C->data[C->tu].col=B->data[j].col; //列
C->data[C->tu].e=B->data[j].e; // 数据
C->tu++;
j++;
}
else //A的col=B的,先把A和B的row和col分别相加,再存入C中
{
if(B->data[j].e+A->data[i].e!=0)
{
C->data[C->tu].row=B->data[j].row; //行
C->data[C->tu].col=B->data[j].col; //列
C->data[C->tu].e=B->data[j].e; // 数据
C->tu++;
}
i++;
j++;
}
}
else //A的row>B的,C中加入B的
{
C->data[C->tu].row=B->data[j].row; //行
C->data[C->tu].col=B->data[j].col; //列
C->data[C->tu].e=B->data[j].e; // 数据
C->tu++;
j++;
}
}
while(itu)//如果A剩余,把A剩余的全放入C中
{
C->data[C->tu].row=A->data[i].row; //行
C->data[C->tu].col=A->data[i].col; //列
C->data[C->tu].e=A->data[i].e; // 数据
C->tu++;
i++;
}
while(jtu)//如果B剩余,把B剩余的全放入C中
{
C->data[C->tu].row=B->data[j].row; //行
C->data[C->tu].col=B->data[j].col; //列
C->data[C->tu].e=B->data[j].e; // 数据
C->tu++;
j++;
}
} 6.三元组表的快速转置
转置定义:将矩阵的行列互换得到的新矩阵称为转置矩阵,转置矩阵的行列式不变。
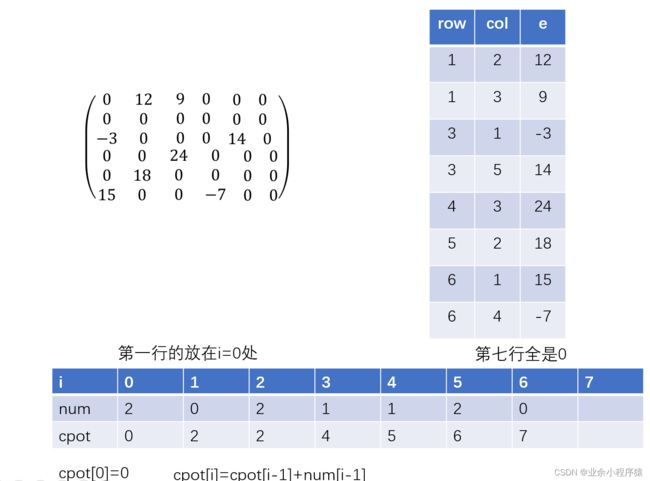
算法思想
矩阵的转置就是讲行列互换位置,如果普通两层循环进行循环的,时间复杂度就会变成![]() ,。所以我们要想办法把只进行一层循环就能完成转置。
,。所以我们要想办法把只进行一层循环就能完成转置。
所以就要设置两个数值num[]和cpot[],num[]用于存储每列非零元素的个数,cpot[]用于存储每列第一个非零元素的初始位置。知道了每列非零元素的初始位置和非零元素的个数,而且列都是按大小来排的,所以转置时候一定的先遇到列数小的先放入,不用担心大小顺序会不同。于是就可以对三元组表进行一次遍历存储。
代码实现
void Transposition(TSMatrix *p,TSMatrix *q)
{
q->nu=p->mu;
q->mu=p->nu;
q->tu=p->tu;//把行列数值对换,大小不变
if(q->tu) //如果三元组为空就不用
{
int i;
int num[100],cpot[100];
for(i=0; imu;i++)
num[i]=0; //初始化数组
for(i=0;itu;i++) //找出每列非零元个数,i=0存的第一列的
++num[p->data[i].col - 1];
cpot[0]=0;
for(i=1;inu;i++) //求每列第一个非零元素所在位置
cpot[i]=cpot[i-1]+num[i-1];
int a,b;
for(i=0;itu;i++) //进行转置
{
b=p->data[i].col-1;
a=cpot[b]; //找出每列所在位置
q->data[a].row = p->data[i].col; //将其放入另外一个三元组表中
q->data[a].col = p->data[i].row;
q->data[a].e = p->data[i].e;
++cpot[b]; //让其下次找到该列中的下一个非零元素
}
}
} 时间复杂度:O(nu+tu)
三元组顺序表又称有序的双下标法,它的特点是,非零元在表中按行序有序存储,因此便于进行依行顺序处理的矩阵运算。然而,若需按行号存取某一行的非零元,则需从头开始进行查找。
7.三元组表输出矩阵
void output(TSMatrix *p)
{
printf("输出矩阵:\n");
int i,j,k=0,a=0;
for(i=1;i<=p->mu;i++){
for(j=1;j<=p->nu;j++)
{
if(p->data[k].row==i&&p->data[k].col==j)
{
printf("%3d",p->data[k].e);
k++;
}
else
printf("%3d",a);
}
printf("\n");
}
}8.全部代码
#include
#include
#define MAX 1000
typedef struct
{
int row,col,e;
}Triple;
typedef struct
{
Triple data[MAX+1];
int mu,nu,tu; //矩阵的行数,列数和非零元个数
}TSMatrix;
void input(TSMatrix *p,int m,int n)
{
int i,j;
int a[100][100];
for( i=1;i<=m;i++)
for(j=1;j<=n;j++)
{
if(1+rand()%4>=1+rand()%19)
a[i][j]=1+rand()%99;
else
a[i][j]=0;
}
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++)
{
printf("%4d",a[i][j]);
}printf("\n");
}
p->tu=0;
for(i=1;i<=m;i++)
for(j=1;j<=n;j++)
{
if(a[i][j]!=0)
{
p->data[p->tu].row=i; //行
p->data[p->tu].col=j; //列
p->data[p->tu].e=a[i][j]; // 数据
++p->tu;
}
}
}
void printTriple(TSMatrix *p)
{
printf("\n三元组:\n");
for(int i=0;itu;i++)
{
printf("%4d %4d %4d\n",p->data[i].row,p->data[i].col,p->data[i].e);
}
}
void sum(TSMatrix *A,TSMatrix *B,TSMatrix *C)
{
C->mu=A->mu;
C->nu=A->nu;
C->tu=0;
if(A->mu!=B->mu&&A->nu!=B->nu){
printf("矩阵要大小相同才能相加!");
return ;
}
int i=0,j=0;
while(itu&&jtu)
{
if(A->data[i].rowdata[j].row)
{
C->data[C->tu].row=A->data[i].row; //行
C->data[C->tu].col=A->data[i].col; //列
C->data[C->tu].e=A->data[i].e; // 数据
C->tu++;
i++;
}
else if(A->data[i].row==B->data[j].row)
{
if(A->data[i].coldata[j].col)
{
C->data[C->tu].row=A->data[i].row; //行
C->data[C->tu].col=A->data[i].col; //列
C->data[C->tu].e=A->data[i].e; // 数据
C->tu++;
i++;
}
else if(A->data[i].col>B->data[j].col)
{
C->data[C->tu].row=B->data[j].row; //行
C->data[C->tu].col=B->data[j].col; //列
C->data[C->tu].e=B->data[j].e; // 数据
C->tu++;
j++;
}
else
{
if(B->data[j].e+A->data[i].e!=0)
{
C->data[C->tu].row=B->data[j].row; //行
C->data[C->tu].col=B->data[j].col; //列
C->data[C->tu].e=B->data[j].e; // 数据
C->tu++;
}
i++;
j++;
}
}
else
{
C->data[C->tu].row=B->data[j].row; //行
C->data[C->tu].col=B->data[j].col; //列
C->data[C->tu].e=B->data[j].e; // 数据
C->tu++;
j++;
}
}
while(itu)
{
C->data[C->tu].row=A->data[i].row; //行
C->data[C->tu].col=A->data[i].col; //列
C->data[C->tu].e=A->data[i].e; // 数据
C->tu++;
i++;
}
while(jtu)
{
C->data[C->tu].row=B->data[j].row; //行
C->data[C->tu].col=B->data[j].col; //列
C->data[C->tu].e=B->data[j].e; // 数据
C->tu++;
j++;
}
}
void Transposition(TSMatrix *p,TSMatrix *q)
{
q->nu=p->mu;
q->mu=p->nu;
q->tu=p->tu;
if(q->tu)
{
int i;
int num[100],cpot[100];
for(i=0; imu;i++)
num[i]=0; //初始化数组
for(i=0;itu;i++)
++num[p->data[i].col - 1];
cpot[0]=0;
for(i=1;inu;i++)
cpot[i]=cpot[i-1]+num[i-1];
int a,b;
for(i=0;itu;i++)
{
b=p->data[i].col-1;
a=cpot[b];
q->data[a].row = p->data[i].col;
q->data[a].col = p->data[i].row;
q->data[a].e = p->data[i].e;
++cpot[b];
}
}
}
void output(TSMatrix *p)
{
printf("输出矩阵:\n");
int i,j,k=0,a=0;
for(i=1;i<=p->mu;i++){
for(j=1;j<=p->nu;j++)
{
if(p->data[k].row==i&&p->data[k].col==j)
{
printf("%3d",p->data[k].e);
k++;
}
else
printf("%3d",a);
}
printf("\n");
}
}
int main()
{
TSMatrix A,B,C,T;
printf("输入A矩阵的行列数:\n");
scanf("%d%d",&A.mu,&A.nu);
input(&A,A.mu,A.nu);
printTriple(&A);
printf("\n输入B矩阵的行列数:\n");
scanf("%d%d",&B.mu,&B.nu);
input(&B,B.mu,B.nu);
printTriple(&B);
sum(&A,&B,&C);
printf("\nC的三元组:\n");
printTriple(&C);
output(&C);
printf("\nA的转置:\n");
Transposition(&A,&T);
printTriple(&T);
output(&T);
getchar();
getchar();
return 0;
}
9.总结
三元组表在考研中,很多自主命题的大学喜欢考这个。在2021年安徽大学计算机专业考研中就出了一个15分的三元组快速转置的大题来考查学生(当年平均分在七八十分左右)。因为对于考生来说,三元组表很少有学生会认真思考,而且王道考研或者是其他考研资料,也很少讲三元组表方面的知识点。所以读者需要加强对三元组表的学习,尤其是快速转置。