OI退役笔记-024：数据结构（四）线段树

引入

线段树是一个恶心的东西

线段树与树状数组类似，可以快速的进行区间修改、区间求值，也可以像 RMQ 一样求区间最值。

概念

线段树是一棵二叉树，每个节点对应一段区间的解。

如图，对于一个数列 A，A[i] = i，i ∈ [0, 8]，则这个数列用线段树储存的情况如图所示。

不难发现，最开始的 [0, 8] 被分成了两份，两个子区间再依次被分成两个区间，直到有区间 [l, r] 满足 l = r 时，该节点是叶子节点，且该点的值可以赋值为 a[l]。

再深入点，我们发现，对于任意区间 [l, r]，当 l = r 时该点为叶子节点，否则该节点有两个子节点。令 mid = (l + r) / 2，则该点的两个子区间分别是 [l, mid]、[mid + 1, r]。

复习二叉树的性质

我的博文里没有二叉树的章节，也许以后会有，但目前来讲需要明确的一点就是二叉树的线性存储。

我们规定二叉树的根节点为 1，则根节点的值储存在 tree[1] 中。再对于这棵二叉树从上到下、从左到右依次编号，则有节点 k 的子节点分别为 (k * 2)、(k * 2 + 1)。

位运算的灵活运用

1. 左移、右移：对于任意整数 a，另 (a << n) = a * 2ⁿ（n ∈ Z）。
2. 按位或：对于任意偶数 a，(a | 1) = a + 1

注意：左移、右移的优先级很低，因此容易犯以下错误：

(j << 1 + 1) = (j << 2) != ((j << 1) + 1)

本篇文章会使用 (k << 1 | 1) 代替 ((k << 1) + 1)。

线段树的实现

线段树的功能有很多，本文以《线段树求区间和》为例。
同时，一下代码中出现的所有数值 k 为当前节点的编号，[l, r] 表示当前区间，[x, y] 表示询问区间。

初始变量

const int N = 1e5+10;
// tree 数组开到 N 的 4 倍 
// 证明略
long long tree[N << 2];
int q[N];

建树

void build(int k, int l, int r)
{
	// 叶子结点直接赋值 
	if (l == r)
	{
		tree[k] = q[l];
		return;
	}
	
	// 不是叶子节点，拆分成两半 
	int mid = (l + r) >> 1;
	build(k << 1, l, mid);
	build(k << 1 | 1, mid + 1, r);
	
	// 更新 
	tree[k] = tree[k << 1] + tree[(k << 1) + 1];
}

单点修改

// 将数列中位置为 x 的数值改为 v
void modify(int k, int l, int r, int x, int v)
{
	// 如果点不包含于当前区间，无需继续搜索 
	if (l > x || r < x)	return;
	
	// 找到了 x 对应的叶子结点，更新 
	if (l == r && l == x)
	{
		tree[k] = v;
		return;
	}
	
	// 剩下的情况即为 x 包含于当前区间，则将当前区间拆分成两半
	// 继续搜索
	int mid = (l + r) >> 1;
	modify(k << 1, l, mid, x, v);
	modify(k << 1 | 1, mid + 1, r, x, v);
	
	// 更新，当前节点存储的是该点所对应区间中所有数的和
	// 也就是两个字区间各自区间内的数值和的总和
	tree[k] = tree[k << 1] + tree[(k << 1) + 1];
}

区间询问

long long query(int k, int l, int r, int x, int y)
{
	// 如果两个区间没有交集，则无需继续递归查询
	if (l > y || r < x)	return 0;
	
	// 如果询问区间包含当前区间
	// 此时返回这段区间的和 
	else if (x <= l && y >= r)
		return tree[k];
	
	// 当前区间不包含于询问区间，但两者有交集
	// 将当前区间分成两半，分别查询并记录的和
	// 直到小区间被询问区间包含 
	int mid = (l + r) >> 1;
	return query(k << 1, l, mid, x, y) + 
		query(k << 1 | 1, mid + 1, r, x, y);
}

举个栗子，对于下面这棵树，求区间 [1, 5] 中所有数的和，就相当于所有蓝色框中数的和：

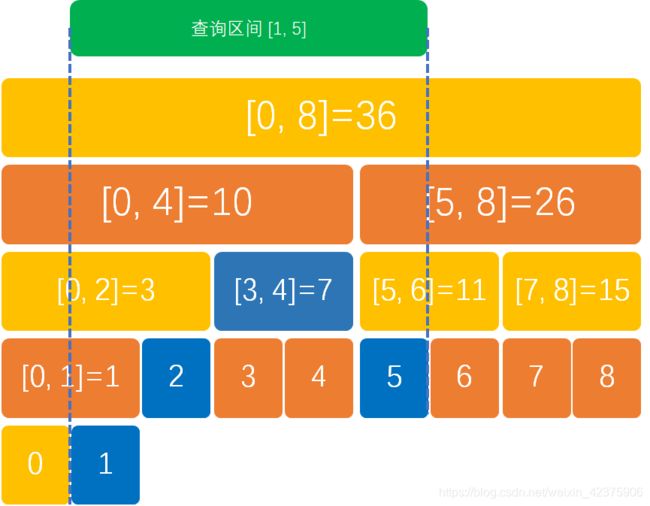
其中 [3, 4] ⊂ [1, 5]，因此 sum 直接加 7，结束递归。
除 [3, 4] 区间外，[0, 2] ∩ [1, 5] ≠ φ，因此将区间 [0, 2] 拆成两部分，继续递归。而对于 [7, 8] 这样的八竿子打不着的区间就不必搜索了。

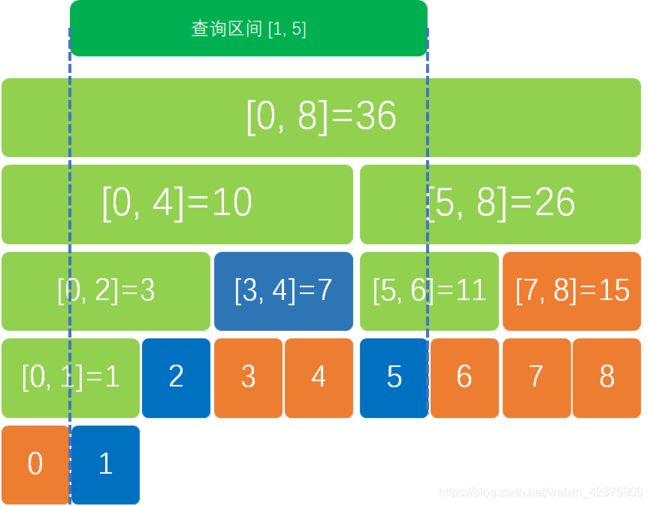
如图，标记为浅绿色和蓝色的即为曾被搜索过的节点。

延迟标记

处理区间修改时，若遍历枚举所有点，则时间复杂度为 O(mnlogn)，明显超时，因此需要换一种方法：

延迟标记：每个节点对应一个 addsum 值，表示该节点 k 所对应区间内每一个数都加上了 addsum[k]。

int addsum[N << 2];

应用延迟标记的区间修改

void modify2(int k, int l, int r, int x, int y, int v)
{
	if (l > y || r < x)	return;
	
	// 包含，说明 [l, r] 区间所有的数都需要 + v
	//  因此只需修改当前节点的 addsum[] 值即可
	if (x <= l && y >= r)
	{
		addsum[k] += v;
		return;
	}
	
	int mid = (l + r) >> 1;
	modify2(k << 1, l, mid, x, y, v);
	modify2(k << 1 | 1, mid + 1, r, x, y, v);
}

应用延迟标记的单点查询

应用延迟标记的单点查询：

运用了延迟标记后，从根节点走到对应区间 [x, x] 的节点的路程中所有的 addsum[] 的和就是答案。证明略。
（看不懂的话再研究一下 modify2() 函数）

int query2(int k, int l, int r, int x)
{
	// 到达叶子结点 
	if (l == r)	return addsum[k];
	
	// x 在哪边就到哪边搜索，返回搜索的值并加上当前节点的 addsum[] 值 
	// 该过程实际上就是二分 
	int mid = (l + r) >> 1;
	if (x <= mid)	return query2(k << 1, l, mid, x) + addsum[k];
	else	return query2(k << 1 | 1, mid + 1, r, x) + addsum[k];
}

对区间修改+区间求值的探讨

最开始的代码就是区间查询的功能，但同时也是仅支持单点修改的。而我们现在的目标是支持区间修改、区间查询，因此还要对数据结构进行升级。

我们发现，在最初的 query() 函数中，求区间和就是求若干段小区间的和。每段小区间的和都有一个节点 k 的值，即 tree[k] 来存储。而在 modify2() 函数中，我们进行区间修改操作时并没有更改 tree[k] 的值，而是修改了 addsum[k] 的值。那么是不是可以将二者结合起来，进而使区间修改后可以区间查询？

答案是肯定的（否定的我还用打这么多字吗）

于是我们用 addsum[k] 表示 k 节点所对应区间每个数都要加的数，tree[k] 对应该区间的区间和。

// 同时维护 tree[] 和 addsum[] 
inline void Add(int k, int l, int r, int v)
{
	// 打标记，表示当前区间下每一个数都 + v 
	addsum[k] += v;
	// 维护当前节点所对应的区间和 
	tree[k] += (r - l + 1) * v;
} 

再看，对节点 k 的区间 [l, r]，令 mid = (l + r) / 2，如果要使区间 [l, mid] 内每一个数都增加 v，那么按照上面的思路直接有：

Add(k << 1, l, mid, v);

可是，如果在进行此操作时 addsum[k] != 0，那么当我们调用 query() 函数求值时，进行到节点 k 后便会直接返回 addsum[k]，而下面的子区间 [l, mid] 压根不会访问。为解决这一问题，我们需要保证每次修改 addsum[k] 时，要保证 k 节点的所有祖先节点的 addsum[] 值都为 0。这样的操作可以用标记下传操作完成。

标记下传（Lazy-Tag，懒标记）

对于 k 节点，如果有 addsum[k] = v，则可以转化为：

addsum[k << 1] = addsum[k];
addsum[k << 1 | 1] = addsum[k];
addsum[k] = 0;

于是我们可以写一个函数：

inline void pushdown(int k, int l, int r, int mid)
{
	// 没有标记，当前节点对应的区间每个数都不需要更改 
	if (!addsum[k])	return;
	
	// 当前节点的左右节点各自的区间都要 + add[k] 
	Add(k << 1, l, mid, addsum[k]);
	Add(k << 1 | 1, mid + 1, r, addsum[k]);
	// 标记清零
	addsum[k] = 0; 
	
	// 于是，父节点的操作信息转移到了左右子节点上 
}

而每次操作只会将标记下传一代（避免不必要的递归），活像驴子一样，你甩下鞭子，它就走两步；你不甩，他也不动。如此的懒惰，使得标记下传的核心就是：懒标记。

应用标记下传的区间修改

void modify3(int k, int l, int r, int x, int y, int v)
{
	// 询问区间包含当前区间，则当前区间每个数 + v 
	if (x <= l && y >= r)	return Add(k, l, r, v);
	
	int mid = (l + r) >> 1;
	// 到达每一个节点都要标记下传 
	// 以保证每次修改的点的祖先节点没有任何标记，避免错误 
	pushdown(k, l, r, mid);
	
	// 此处用逆向思维思考一下：
	// 当 x > mid 时 [l, mid] ∩ [x, y] = φ，不用继续递归
	if (x <= mid)	modify3(k << 1, l, mid, x, y, v);
	// 同理
	if (y > mid)	modify3(k << 1 | 1, mid + 1, r, x, y, v);
	
	tree[k] = tree[k << 1] + tree[k << 1 | 1];
}

应用标记下传的区间查询

// 注释略，基本思想与前面相同
long long query3(int k, int l, int r, int x, int y)
{
	
	if (x <= l && y >= r)	return tree[k];
	
	int mid = (l + r) >> 1;
	pushdown(k, l, r, mid);
	long long ans = 0;
	if (x <= mid)	ans += query3(k << 1, l, mid, x, y);
	if (y > mid)	ans += query3(k << 1 | 1, mid + 1, r, x, y);
	
	return ans;
} 

线段树与其他类似算法的比较

1. 线段树与树状数组的比较：

• 线段树的单次操作时间复杂度为 O(logn)
• 线段树求解更优，但常数较大，代码更为复杂
• 树状数组能承受的数量级大概在 1e6 以内

2. 线段树与平衡树的比较

• 平衡树能支持更多的操作，但代码更为复杂
• 学完线段树你不会有兴趣学平衡树的

3. 线段树与分块的比较

• 分块的复杂度为 O(sqrt(n))
• 但分块易于拓展

[2021-06-03] 补充：

代码：

#include 

inline int max(int a, int b)
  {return (a > b) ? a : b;}

int n, m, a, last, p, tree[800001];
char ch;

void modify(int k, int l, int r, int x, int v)
{
	if (l > x || r < x)	return;
	
	if (l == r && l == x)
	{
		tree[k] = v;
		return;
	}
	
	int mid = (l + r) >> 1;
	modify(k << 1, l, mid, x, v);
	modify(k << 1 | 1, mid + 1, r, x, v);
	
	tree[k] = max(tree[k << 1], tree[k << 1 | 1]);
}

int query(int k, int l, int r, int x, int y)
{
	if (l > y || r < x)	return 0;
	
	if (x <= l && y >= r)
		return tree[k];
	
	int mid = (l + r) >> 1;
	return max(query(k << 1, l, mid, x, y),
		query(k << 1 | 1, mid + 1, r, x, y));
}

int main()
{
	scanf("%d%d", &m, &p);
	
    for (int i = 1; i <= m; ++i) {
    	
        scanf("%c%c%d", &ch, &ch, &a);
        
        if (ch == 'Q')
		{
            last = query(1, 1, m, n - a + 1, m) % p;
            printf("%d\n", last);
        }
		else
		{
			++n;
            modify(1, 1, m, n, (last + a) % p);
        }
    }
}

这道题的特殊之处在于操作是“在末尾插入”。但可以换一个思路：建一棵比较大的线段树，部分值设为 0，在末尾插入相当于modify 一下 n + 1 位置的数。
但要注意的是：线段树的区间是定值，即注意这一行代码初始区间是 [1, m]。而改成 [1, n] 会出错。线段树一旦建起，每次操作的初始区间绝对不能变，否则就会出错。

last = query(1, 1, m, n - a + 1, m) % p;

简单解释： 对于根节点，其区间若发生改变，则其所有子区间也会随之改变。而子区间改变后，tree[i] 所对应的区间也会改变，而值没变（无法改变），因此会出错。

作者：Rotch
日期：2021-06-01
修改：2021-06-01