数据结构-二叉树及其应用
- 实验项目名称
二叉树及其应用
- 实验要求
树是数据结构中应用极为广泛的非线性结构,本单元的实验达到熟悉二叉树的存储结构的特性,以及如何应用树结构解决具体问题。
- 实验内容
利用二叉树求解表达式的值。
- 算法分析
void EXTInitStack(ETLinkStack& LS)// 树栈初始化
{
LS = NULL;
}
void EXTPush(ETLinkStack& LS, ExpTree ET)// 树栈添加元素
{
ETStackNode* p = new ETStackNode;
p->ETStackdata = ET;
p->next = LS;
LS = p;
}
void EXTPop(ETLinkStack& LS, ExpTree& ET)// 树栈弹出栈顶元素
{
if (LS == NULL) return;
ET = LS->ETStackdata;
ETStackNode* p = LS;
LS = LS->next;
delete p;
}
ExpTree EXTGetTop(ETLinkStack& LS)// 树栈获取栈顶元素
{
if (LS) return LS->ETStackdata;
}
对树栈的相关操作,基本的包括创建栈,添加元素,删除元素,获取栈顶元素。
void ChInitStack(ChLinkStack& CS)// 算符栈初始化
{
CS = NULL;
}
void ChPush(ChLinkStack& CS, ElemType e)// 算符栈添加元素
{
ChStackNode* p = new ChStackNode;
p->ChStackdata = e;
p->next = CS;
CS = p;
}
void ChPop(ChLinkStack& CS, ElemType& e)// 算符栈弹出栈顶元素
{
if (CS == NULL) return;
e = CS->ChStackdata;
ChStackNode* p = CS;
CS = CS->next;
delete p;
}
ElemType ChGetTop(ChLinkStack& CS)// 算符栈获取栈顶元素值
{
if (CS != NULL) return CS->ChStackdata;
}
对算符栈的基本操作,包括创建栈,添加元素,删除元素,获取栈顶元素。
bool In(char ch)// 判断ch是否为算符
{
int i = 0;
while (Op && Op[i] != ch)
i++;
return i < 7;
}
void CreateExpTree(ExpTree& T, TreeNode* lchild, TreeNode* rchild, TreeElemType data)// 创建表达式树结点
{
T = new TreeNode;
T->data = data;
T->lchild = lchild;
T->rchild = rchild;
}
char Precede(char c1, char c2)// 判断算符优先级
{
int i = 0, j = 0;
while (Op[i] && Op[i] != c1)
i++;
while (Op[j] && Op[j] != c2)
j++;
return CList[i][j];
}
杂项操作,包括判断算符优先级,是否为算符等。
ExpTree InitExpTree()// 表达式树的创建算法
{
ETLinkStack EXPT;
ChLinkStack OPTR;
EXTInitStack(EXPT);
ChInitStack(OPTR);
ChPush(OPTR, '=');
char ch;
cin >> ch;
while (ch != '=' || ChGetTop(OPTR) != '=')
{
if (!In(ch))
{
char data[20] = { '\0' };
int i = 0;
data[i++] = ch;
cin >> ch;
while (!In(ch))
{
data[i++] = ch;
cin >> ch;
}
ExpTree T;
CreateExpTree(T, NULL, NULL, atof(data));
EXTPush(EXPT, T);
}
else
{
switch (Precede(ChGetTop(OPTR), ch))
{
case '<':
ChPush(OPTR, ch);
cin >> ch;
break;
case '>':
char theta;
ChPop(OPTR, theta);
TreeNode* t1, * t2;
EXTPop(EXPT, t2); EXTPop(EXPT, t1);
ExpTree T;
CreateExpTree(T, t1, t2, theta);
EXTPush(EXPT, T);
break;
case '=':
ChPop(OPTR, theta);
cin >> ch;
break;
}
}
}
return EXTGetTop(EXPT);
}
创建表达式树:通过算符优先级表得出各算符优先级,时间复杂度O(n)。
double GetValue(char ch, double a, double b)// 求值
{
switch (ch)
{
case '+':
return a + b;
case '-':
return a - b;
case '*':
return a * b;
case '/':
return a / b;
}
}
double EvaluateExpTree(ExpTree T)// 遍历表达树进行表达式求值
{
double lvalue = 0, rvalue = 0;
if (T->lchild == NULL && T->rchild == NULL)
return T->data;
else
{
lvalue = EvaluateExpTree(T->lchild);
rvalue = EvaluateExpTree(T->rchild);
return GetValue(T->data, lvalue, rvalue);
}
}
表达式求值:通过后序遍历表达式树得出相应的后缀表达式,之后求值就简单了。
int main()// 主函数
{
cout << "请输入运算表达式:" << endl;
ExpTree T = InitExpTree();
cout << "该运算表达式值为:" << EvaluateExpTree(T) << endl;
return 0;
}
主函数
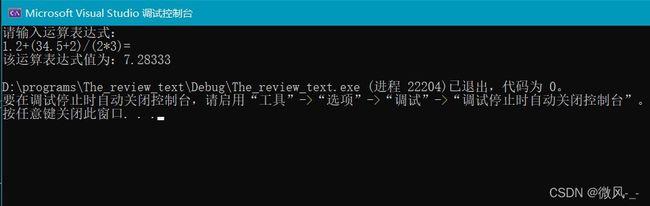
- 实验结果
- 思考体会
|