数据结构--二叉树的递归遍历

系列文章目录

第七话 数据结构之二叉树

文章目录

• 一、了解什么是二叉树
• 二、二叉树的基本特征
• 三、二叉树的定义
  • 二叉树的基本操作
  • 二叉树的初始化
  • 二叉树的递归遍历
• 四、总结

---

前言

人人都见过树，知道树可以调节气候、净化空气、防风降噪、防止水土流失和山体滑坡等自然灾害，是人类的好朋友。那么在程序设计和数据结构中，树如何存在和发挥作用呢？树从上到下主要成分为树叶、树枝、树干、树根，这四部分构成了所有树共同具有的结构：根、分支、叶子。人类社会的很多管理层次架构都可以用树结构来表示，树结构是以分支关系定义的层次结构，在软件开发与设计领域的应用非常广泛。

一、了解什么是二叉树

二叉树是一种特殊的树结构，也是最常用的树结构。二叉树的存储和处理比一般的树简单，而一般的树都能通过转换得到与之对应的二叉树，因此解决树的有关问题就可以借助于二叉树来实现。

二、二叉树的基本特征

二叉树是n个节点的有限集合，对于非空树T；

1、有且仅有一个称为根的节点；

2、除根节点以外的其余节点分别由两个不相交的、被分别称为左子树和右子树的二叉树组成。

3、二叉树中每个节点的度不大于2；

4、二叉树是有序的，其子树有左右之分，其次序不能任意颠倒。

三、二叉树的定义

1、二叉树的几种情况

2、二叉树的存储结构--顺序存储

#include 
#include 
#define maxsize 100
typedef char Elemtype;
typedef struct node{
    Elemtype date[maxsize];
    struct node *lchild,*rchild;
}bitree;

3、二叉树的创建

bitree *creatbitree()
{
    //创建二叉树
    bitree *pA = (bitree*)malloc(sizeof(bitree));
    bitree *pB = (bitree*)malloc(sizeof(bitree));
    bitree *pC = (bitree*)malloc(sizeof(bitree));
    bitree *pD = (bitree*)malloc(sizeof(bitree));
    bitree *pE = (bitree*)malloc(sizeof(bitree));
    bitree *pF = (bitree*)malloc(sizeof(bitree));
    bitree *pG = (bitree*)malloc(sizeof(bitree));
    //给二叉树赋值
    pA->date = 'A';
    pB->date = 'B';
    pC->date = 'C';
    pD->date = 'D';
    pE->date = 'E';
    pF->date = 'F';
    pG->date = 'G';
    //给二叉树左右孩子赋值
    pA->lchild = pB;
    pA->rchild = pC;
    
    pB->lchild = NULL;
    pB->rchild = pD;
    
    pC->lchild = NULL;
    pC->rchild = pE;
    
    pD->lchild = pF;
    pD->rchild = pG;
    
    pE->lchild = NULL;
    pE->rchild = NULL;
    
    pF->lchild = NULL;
    pF->rchild = NULL;
    
    pG->lchild = NULL;
    pG->rchild = NULL;
}

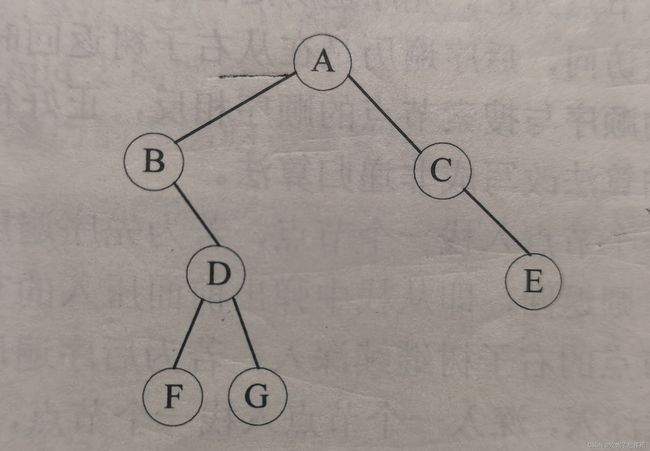
创建的树的样子为: 

 

需要实现的操作为：

 

4、二叉树的先序遍历（递归）

//先序遍历（递归）
void preorder(bitree *t)
{
    if(t != NULL){//方法：先根再左再右
        printf("%c ",t->date);
        preorder(t->lchild);//遍历左子树
        preorder(t->rchild);//遍历右子树
    }
}

在主行数中实现调用

int main()
{
    bitree *t;
    t = creat_bitree();
    printf("先序遍历：");
    preorder(t);
    printf("\n");
    return 0;
}

5、二叉树的中序遍历（递归） 

//中序遍历
void inorder(bitree *t)
{
    if(t!=NULL){
        inorder(t->lchild);//先遍历左子树
        printf("%c ",t->date);
        inorder(t->rchild);//遍历右子树
    }
}

6、二叉树的后序遍历（递归）

void postorder(bitree *t)
{
    if(t!=NULL){//先左再右再根
        postorder(t->lchild);
        postorder(t->rchild);
        printf("%c ",t->date);
    }
}

 在主行数中实现调用

int main()
{
    bitree *t;
    t = creat_bitree();
    printf("先序遍历：");
    preorder(t);
    printf("\n");
    printf("中序遍历：");
    inorder(t);
    printf("\n");
    printf("后序遍历: ");
    postorder(t);
    printf("\n");
    return 0;
}

 

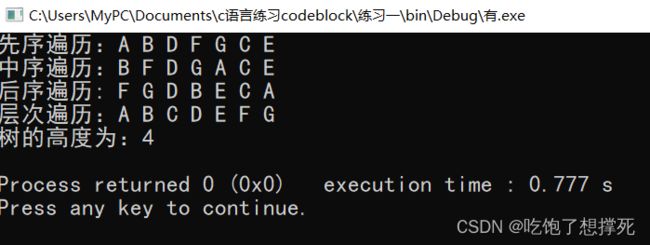
7、二叉树的层次遍历

void levelorder(bitree *t)
{
    //创建队列
    bitree *Queue[maxsize];
    int front = 0;
    int rear = 0;
    //当节点不为0时入队
    if(t!=0){
        Queue[rear++] = t;
    }
    //当队列没满时
    while(front!=rear)
    {
        bitree *ch = Queue[front++];//出队
        printf("%c ",ch->date);
        if(ch->lchild!=NULL){
            Queue[rear++] = ch->lchild;//左子树出队
        }
        if(ch->rchild!=NULL){
            Queue[rear++] = ch->rchild;//右子树出队
        }
    }
}

 

8、求二叉树的高度 

//树的高度
int depthbitree(bitree *t)
{
    int m,n;
    //空树的高度为0
    if(t==NULL){
        return 0;
    }else{
        m = depthbitree(t->lchild);//求左子树的高度
        n = depthbitree(t->rchild);//求右子树的高度
    }
    if(m>n){
        return m+1;
    }else{
        return n+1;
    }
}

 

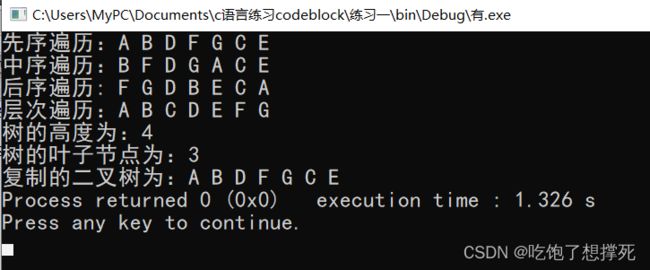
 9、统计二叉树叶子节点个数

当二叉树为空时，叶子节点个数为0；当二叉树只有一个根节点时，根节点就是叶子节点，叶子节点个数为1；在其他情况下，计算左子树与右子树中的叶子节点的和

//统计二叉树中叶子节点个数
int countbitree(bitree *t)
{
    int m,n;
    if(t==NULL){
        return 0;
    }
    //左右子树都为空时
    if(t->lchild==NULL&&t->rchild==NULL){
        return 1;
    }else{
        m = countbitree(t->lchild);
        n = countbitree(t->rchild);
        return (m+n);
    }
}

 

10、复制二叉树 

 复制二叉树就是利用已有的一颗二叉树复制得到另外一颗与其完全相同的二叉树，其复制步骤如下：

若二叉树不空，则首先复制根节点，然后分别复制二叉树根节点的左子树和右子树，其实现过程与二叉树先序遍历的实现类似

//复制二叉树
void copybitree(bitree *t1,bitree *t2)
{
    //二叉树为空
    if(t1==NULL){
        t2 = NULL;
    }else{//二叉树不为空
        t2 = (bitree*)malloc(sizeof(bitree));
        t2->date = t1->date;
        printf("%c ",t2->date);
        copybitree(t1->lchild,t2->lchild);//复制左子树
        copybitree(t1->rchild,t2->rchild);//复制右子树
    }
}

 在主行数中实现调用

int main()
{
    bitree *t;
    t = creat_bitree();
    printf("先序遍历：");
    preorder(t);
    printf("\n");
    printf("中序遍历：");
    inorder(t);
    printf("\n");
    printf("后序遍历: ");
    postorder(t);
    printf("\n");
    printf("层次遍历：");
    levelorder(t);
    printf("\n");
    printf("树的高度为：");
    int a = depthbitree(t);
    printf("%d\n",a);
    printf("树的叶子节点为：");
    int b = countbitree(t);
    printf("%d\n",b);
    printf("复制的二叉树为：");
    bitree *t2;
    copybitree(t,t2);
    return 0;
}

 

---

四、总结

在二叉树的操作实现中，常常需要对其所有节点进行某种操作，这种对所有节点逐一进行的操作就是遍历。

二叉树除了递归遍历，还需要掌握非递归遍历，想要了解请看下章！