二叉树链式存储结构
目录
1.二叉树链式存储结构
2.二叉树的遍历
2.1 前、中、后序遍历
2.2 层序遍历
3.二叉树的其他递归问题
3.1 二叉树的结点个数
3.2 二叉树的叶子结点个数
3.3 二叉树第k层结点个数
3.4 二叉树的深度
3.5 二叉树查找
3.6 二叉树销毁
4.二叉树的基础OJ题
4.1 单值二叉树
4.2 检查两棵树是否相同
4.3 对称二叉树
4.4 另一棵树的子树
4.5 二叉树翻转
4.6 二叉树的前序遍历
4.7 二叉树的中序遍历
4.8 二叉树的后序遍历
4.9 二叉树的创建
1.二叉树链式存储结构
在此之前我们先复习一下二叉树的概念：
二叉树是：
-
空树
-
非空：根结点，根结点的左子树，根结点的右子树组成
从二叉树的定义中，我们可以发现二叉树是递归式定义的（一颗二叉树由根，左子树和右子树组成，左子树又是由根，左子树，右子树组成...依次递归），因此后面有关二叉树的操作都是根据递归实现的。
二叉树的链式存储结构是指，用链表来表示一棵二叉树，即用链来指示元素的逻辑关系。通常的方法是链表中每个结点由三个域组成，数据域和左右指针域，左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址。链式结构又分为二叉链和三叉链，当前我们学习中一般都是二叉链。高阶二叉树(AVL树、红黑树)会用到三叉链。 
typedef char BTDataType;
//二叉链表
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;
//三叉链表
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* parent;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;说明：由于普通二叉树存储数据没有任何意义，不如直接存储在线性表中，所以我们不关心他的增删查改，只关注他的递归遍历结构（高阶二叉树，如二叉树搜索树、AVL树、红黑树研究增删查改）。
2.二叉树的遍历
2.1 前、中、后序遍历
学习二叉树结构，最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。遍历是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。
按照规则，二叉树的遍历有:前序/中序/后序的递归结构遍历:
-
前序遍历(Preorder Traversal亦称先序遍历)――访问根结点的操作发生在遍历其左右子树之前。
-
中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间）。
-
后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。
由于被访问的结点必是某子树的根，所以N(Node）、L(Left subtree）和R(Right subtree）又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。
代码实现：
void PreOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
printf("%c ", root->data);
PreOrder(root->left);
PreOrder(root->right);
}
void InOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
InOrder(root->left);
printf("%c ", root->data);
InOrder(root->right);
}
void PostOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%c ", root->data);
}这三个递归遍历的代码看似简单，但是对于初学者的人来说并不是特别好理解他其中递归层次的变化。
下面主要分析前序递归遍历，中序与后序类似。
前根遍历递归图解：
前根遍历代码的递归展开图：
对于初学二叉树递归的人来说，画代码的递归展开图是最好的理解方式，不理解的代码画一画展开图就会一目了然。
2.2 层序遍历
除了先序遍历、中序遍历、后序遍历外，还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的树根节点，然后从左到右访问第2层上的节点，接着是第三层的节点，以此类推，自上而下，自左至右逐层访问树的结点的过程就是层序遍历。
如何进行层次遍历？这就要用到前面所学的队列这种数据结构了，详细见：栈和队列实现
接下来我们说说队列实现层次遍历算法设计思路：
使用一个队列
-
第一步：将根结点进队；
-
第二步：控制一个循环，队列不空时，取队头结点，Pop掉这个队头结点并访问他：
若他有左孩子结点，将左孩子结点进队；
若他有右孩子结点，将右孩子结点进队；
每次循环访问队头元素时，都是访问当层结点，而当层结点的左右孩子都是下一层结点，这些孩子结点进队列后等待访问，这样就可以做到层次遍历。
下面就是层次遍历的代码实现；
需要注意的一点是，队列存储的是树的结点，还是结点的val值呢？很明显是树的结点，因为我们还要将节点的左右孩子入队，这就需要访问节点的左右孩子。
那么队列存储的数据类型为结点的数据类型，结点的数据类型是我们自定义的数据类型BTNode*,但是编译器只认识内置数据类型，我们有两种方式来解决：1.进行前置声明 2.头文件声明位置放在BTNode类型声明的下面，如：
struct BinaryTreeNode;
typedef struct BinaryTreeNode* QDataType;
typedef struct QueueNode
{
QDataType data;
struct QueueNode* next;
}QueueNode;void LevelOrder(BTNode* root)
{
Queue q;
QueueInit(&q);
//根节点入队
if(root)
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
//取队头结点（当层结点），访问并Pop
BTNode* front = QueueFront(&q);
QueuePop(&q);
printf("%d ", front->val);
//左右孩子不为空，入队列
if (front->left)
QueuePush(&q, front->left);
if (front->right)
QueuePush(&q, front->right);
}
printf("\n");
QueueDestory(&q);
}
下面我们根据这个层次遍历来实际解决一个衍生问题：判断一个树是否为完全二叉树
我们就可以利用测那层次遍历来解决这个问题：
我们来看一下完全二叉树和非完全二叉树他们在层次遍历时队列变化有什么区别：
（这里的层次遍历我们带上空结点，图中空结点用#表示）
可以大概了解出：
完全二叉树层次遍历遇到空结点后，后面全是空结点。
非完全二叉树遇到空结点后，后面有非空结点。
我们根据这点来实现代码：
bool IsComplete(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root)
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
//front为空，说明遇到空结点，break
if (!front)
break;
//这里同层序遍历不同的是，空结点也要入队
QueuePush(&q, front->left);
QueuePush(&q, front->right);
}
while(!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
//说明空结点后有非空结点，返回false
if (front)
{
QueueDestory(&q);
return false;
}
}
//空结点后全是空结点，返回true
QueueDestory(&q);
return true;
}注：代码相比于层序遍历不同的是，空结点也是要入队的。其次是要注意队列销毁的时机。
3.二叉树的其他递归问题
二叉树的其他递归问题，主要有以下这些：
二叉树的结点个数
二叉树的叶子结点个数
二叉树第k层结点个数
二叉树的深度
二叉树查找
这些问题相对遍历递归，对递归的理解又有了更进一步的的要求。
关于递归，我们先看定义：
递归是一种算法或函数调用自身的方式。在递归的过程中，问题被分解为更小的子问题，直到达到基本情况（终止条件），然后通过将子问题的解合并成原始问题的解来解决问题。
递归的实现通常包括两个部分：
递归终止条件：确定何时停止递归，防止无限循环。这通常是在问题达到某种简单形式或特定值时。
递归调用：在解决问题的过程中，将问题分解为更小的子问题，并通过调用自身来解决这些子问题。
递归算法的优点是可以简化问题的解决方式，使代码更具可读性和简洁性。但是，递归算法也有一些潜在的问题：
递归算法可能会导致性能问题，因为每次递归调用都需要创建新的函数调用栈。
如果递归调用的层次太深，可能会导致栈溢出的问题。
递归算法的实现可能会比迭代算法更复杂。
递归的一些常见应用包括：树的遍历，排序算法（如归并排序、快速排序）、动态规划和回溯等。
在使用递归时，需要注意选择合适的终止条件和避免无限循环。此外，递归算法也可以通过迭代的方式重新实现，以提高性能和减少内存消耗。
总的来说，递归就是将一个问题分解成更小的子问题，一直分解一直分解，直到这个子问题能够被直接解决，这种子问题也就是最小子问题，也叫做递归的终止条件。
对于绝大多数的二叉树递归问题，最小子问题一般都是空树。（并不是全部，只是占多数）
3.1 二叉树的结点个数
这个问题也可以不用递归来解决，我们可以用一个全局变量或者局部静态变量来记录结点数count，然后先根遍历对count进行++，或者传count计数变量的指针也是可以的，但是这些方法明显都比较挫，就比如局部静态变量计数，这种变量只能记录一次节点总数，计数完之后要置空，就非常麻烦。所以我们讲解一下递归解法：
递归终止：root == NULL ，结点个数为0；
递归调用：root != NULL，结点个数 == 1（根结点） + 左子树结点个数 + 右子树结点个数
左右子树的结点个数可以分解成子问题。
int BinaryTreeSize(BTNode* root)
{
return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}
我们来画他的递归展开图，便于理解：
3.2 二叉树的叶子结点个数
叶子结点：没有左右孩子，root->left == NULL && root->right ==NULL
递归终止：
root == NULL ，没有叶子结点；
root != NULL， root->left == NULL && root->right ==NULL：这棵树就是一个叶子结点；
递归调用：
root != NULL 并且 不是叶子结点，叶子结点个数 == 左子树叶子结点个数 + 右子树叶子结点个数；
左右子树的叶子节点数可以分解成子问题。
int BinaryTreeLeafSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
if (root->left == NULL && root->right == NULL)
{
return 1;
}
return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}3.3 二叉树第k层结点个数
递归终止：
root == NULL : 空树，第k层结点个数为0
root != NULL && k == 1 :第一层为根结点，结点个数为1
递归调用：
root !=NULL && k>1 : 第k层结点个数 == 左子树第k - 1 层结点个数 + 右子树第k - 1 层结点个数
左右子树第k - 1 层结点个数可以分解成子问题
int BinaryTreeLevelKSize(BTNode* root,int k)
{
assert(k >= 1);
if (root == NULL)
{
return 0;
}
if (k == 1)
{
return 1;
}
return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}3.4 二叉树的深度
递归终止：
root == NULL : 深度为0
递归调用：
root != NULL : 深度 == 左右子树中深度较大的 + 1
左右子树深度可以分解成子问题
int BinaryTreeDepth(BTNode* root)
{
if (root == NULL)
{
return 0;
}
else
{
//不要用这种方式，BinaryTreeDepth反复调用，表达式比较时候调用，后面又调用一次,对栈帧的消耗比较大
//return BinaryTreeDepth(root->left) > BinaryTreeDepth(root->right)
// ? BinaryTreeDepth(root->left) + 1
// : BinaryTreeDepth(root->right) + 1;
//这里最好用一个变量保存起来
int leftDepth = BinaryTreeDepth(root->left);
int rightDepth = BinaryTreeDepth(root->right);
return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}
}注意：就像代码中所写的那样，我们要避免递归函数的重复调用，毕竟每一次递归函数的调用都是对函数栈帧的一个大消耗，所以这个问题要注意。
3.5 二叉树查找
递归终止：
root == NULL : 空树，查找失败
root != NULL && root->val == x : 查找成功
递归调用：
root != NULL && root->val != x : 去左子树和右子树中查找
左右子树的查找可以分解成子问题
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
{
return NULL;
}
if (root->data == x)
{
return root;
}
//这里和上一个函数是一个道理，要保存结果，不然函数反复调用
//if (BinaryTreeFind(root->left,x))
//{
// return BinaryTreeFind(root->left, x);
//}
//if (BinaryTreeFind(root->right, x))
//{
// return BinaryTreeFind(root->right, x);
//}
//不建议这样写，因为如果在左子树中找到了，右子树中就白找了
//BTNode* leftRet = BinaryTreeFind(root->left, x);
//BTNode* rightRet = BinaryTreeFind(root->right, x);
//if (leftRet)
//{
// return leftRet;
//}
//else
//{
// return rightRet;
//}
//先找左子树,左子树找到了直接返回，不用在右子树里面找
BTNode* leftRet = BinaryTreeFind(root->left, x);
if (leftRet)
return leftRet;
BTNode* rightRet = BinaryTreeFind(root->right, x);
if (rightRet)
return rightRet;
return NULL;
}注意：
这种代码有两个注意点，一个就是上面所说的函数重复调用问题，还有一个就是左右子树递归调用的顺序问题，假如左子树找到了，我们就不需要在右子树里面找了。
3.6 二叉树销毁
二叉树销毁最好的方式是后序遍历，避免找不到左右子树，根放在后面销毁。（当然也可以不用后序，就像链表头删一样，先用个变量保存左右子树再销毁根也是可行的）。
void BinaryTreeDestory(BTNode* root)
{
if (!root)
return;
BinaryTreeDestory(root->left);
BinaryTreeDestory(root->right);
free(root);
}4.二叉树的基础OJ题
4.1 单值二叉树
bool isUnivalTree(struct TreeNode* root){}检查一棵树root是否为单值二叉树，也就是判断根结点的val是否和左右子树根结点的val相等，然后再分解成左右子树问题，绝大多数人会先想到用这种方法来判断：
if(root->val == root->left->val && root->val == root->right->val)
return true;但是这个代码真的能解决问题吗？显然不可以！这个代码有两个问题：
根结点的val和左右子树根结点的val相等，就是单值二叉树了吗？就能直接返回true了吗？显然不能！
能一定保证root != NULL？如果root为NULL，是不是编译出错？
递归终止：
root == NULL :空树，返回true（说明递归到底了）
root != NULL 并且 root->val != root->left->val || root->val != root->right->val:不是单值，返回false（注意：root->left和root->right不能为空）
递归调用：
root != NULL 并且 root->val == root->left->val && root->val == root->right->val ：根结点符合单值条件，再判断左右子树是否为单值
左右子树的单值问题可以分解为子问题
bool isUnivalTree(struct TreeNode* root)
{
if(root == NULL)
return true;
//左子树不为空且根的val和左子树的根的val不同
if(root->left && root->val != root->left->val)
return false;
//右子树不为空且根的val和右子树的根的val不同
if(root->right && root->val != root->right->val)
return false;
return isUnivalTree(root->left) && isUnivalTree(root->right);
}4.2 检查两棵树是否相同
bool isSameTree(struct TreeNode* p, struct TreeNode* q){}检查两棵树是否相同，从递归思想来看，可以先判断根结点是否相等，在递归判断左右子树。
但是这种想法是错误的！不相等的两棵树，不单单是结点的val不相等，还有可能是树的形状不同，也就是两边结点一个为空一个不为空。
树的形状不同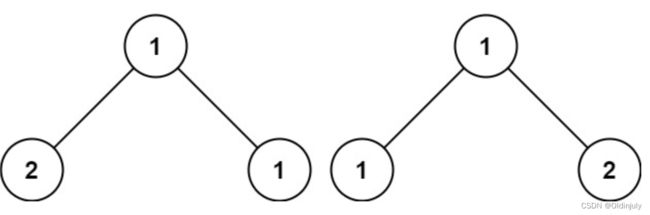 
结点val不同
递归终止：
p == NULL && q == NULL:两个结点都为空，返回true
p == NULL || q == NULL:一个结点为空，一个结点不为空,返回false
p != NULL && q != NULL, p->val != q->val:两个结点都不为空，并且结点的值不同,返回false
递归调用：
p != NULL && q != NULL, p->val == q->val:这两个结点都不为空，并且结点的值相同，递归判断他们左右子树是否相等
左右子树的相等问题可以分解成子问题
//判断两棵树是否相等，先判断根是否相等，再递归判断左右子树是否相等
bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
/*
if(p->val == q->val)
return true;
*/
//上面这种代码不能解决问题，首先只有根相等并不能断定他们相等，其次我们并不知道p或者q是否为NULL
//但是根结点不相等我们能直接判断两棵树不相等，其次我们要讨论结点为NULL的情况
//两个根结点都为NULL
if(p == NULL && q == NULL)
return true;
//两个根结点一个为NULL，一个不为NULL,两棵树必定不相等
//（两个都为NULL也能进if语句里面，但是两个都为NULL一定先进上面的if语句里面）
if(p == NULL || q == NULL)
return false;
//两个根结点都不为NULL，并且val值不相等,两棵树必定不相等
if(p->val != q->val)
return false;
//两个根结点都不为NULL，val值相等,说明根相等，在递归判断左右子树是否相等
return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}4.3 对称二叉树
bool isSymmetric(struct TreeNode* root){}
判断一棵树是否为对称二叉树，可以转换成这棵二叉树的左右子树是否对称，而判断两棵树是否对称，是不是类似判断两棵树是否相等？
判断两棵树相等：p的左 == q的左 && p的右 == q的右
判断两棵树对称：p的左 == q的右 && p的右 == q的左
bool _isSymmetric(struct TreeNode* p, struct TreeNode* q){} 递归终止：
p == NULL && q == NULL:两个结点都为空，返回true
p == NULL || q == NULL：一个结点为空，一个结点不为空，不对称返回false
p != NULL && q != NULL, p->val != q->val:两个结点都不为空，并且结点的值不同,返回false
递归调用：
p != NULL && q != NULL, p->val == q->val:这两个结点都不为空，并且结点的值相同，递归判断他们左右子树是否对称
左右子树的对称问题可以分解成子问题
//两棵树对称：p的左 == q的右 && p的右 == q的左
bool _isSymmetric(struct TreeNode* p, struct TreeNode* q)
{
if(p == NULL && q == NULL)
return true;
if(p == NULL || q == NULL)
return false;
if(p->val != q->val)
return false;
return _isSymmetric(p->left, q->right) && _isSymmetric(p->right, q->left);
}
//一棵树是否对称，转换为这棵树的左右子树是否对称
bool isSymmetric(struct TreeNode* root)
{
return _isSymmetric(root->left, root->right);
}4.4 另一棵树的子树
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){}判断树q是否为树p的子树，从递归的思想来看，可以先判断p树和q树是否相等，如果不相等，递归判断p的左右子树是否和q相等即可。
递归终止：
p == NULL：p树递归到空，q不是p的子树，返回false
p != NULL && p == q：q是p的子树，返回true
递归调用：
p != NULL && p != q：不相等，递归判断p的左右子树是否和q相等
判断p的左右子树是否包含 q，可以分解成子问题
bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
if(p == NULL && q == NULL)
return true;
if(p == NULL || q == NULL)
return false;
if(p->val != q->val)
return false;
return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}
//判断p树是否为q树的子树，先判断p树和q树是否相等，不相等的话再递归q的左右子树和p是否相等
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot)
{
//q为空，不相等
if(root == NULL)
return false;
//判断p树和q树是否相等
if(isSameTree(root, subRoot))
return true;
//p树和q树不相等,递归q的左右子树和p是否相等
return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
}4.5 二叉树翻转
翻转一个二叉树即交换这棵二叉树的左右子树。
递归终止：
root == NULL : 为空，没有左右子树，不用翻转。
递归调用：
root != NULL : 不为空，交换左右子树，再递归翻转左右子树。
左右子树的翻转问题分解成子问题。
void _invertTree(struct TreeNode* root)
{
if(root == NULL)
return;
struct TreeNode* temp = root->left;
root->left = root->right;
root->right = temp;
_invertTree(root->left);
_invertTree(root->right);
}
struct TreeNode* invertTree(struct TreeNode* root)
{
_invertTree(root);
return root;
}4.6 二叉树的前序遍历
这题要求把遍历的结点val值以数组的形式返回，不同于简单的遍历，但是逻辑和普通的遍历没有太大的区别，主要考察递归调用中局部变量的变化情况。
我们要把结点的val值读入数组中，这里就需要一个变量i来标识数组的下标，但是这里的i就有陷阱了，这也是递归问题中一个常见的问题。
这里的i必须传地址，因为对于递归问题来说，每一层函数栈帧的i都是独立的局部变量，每一层的i都不相等，递归回退上一层后，i值不是原来的i了。
int TreeSize(struct TreeNode* root)
{
return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
//这里的i必须传地址，因为对于递归问题来说，每一层函数栈帧的i都是独立的局部变量，并不相等，递归回退上一层后，i值不是原来的i了
void _preorderTraversal(struct TreeNode* root, int* arr, int* pi)
{
//root为空
if(!root)
return;
//root不为空，val值放入数组
arr[(*pi)++] = root->val;
_preorderTraversal(root->left, arr, pi);
_preorderTraversal(root->right, arr, pi);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize)
{
int size = TreeSize(root);
int* retArr = (int*)malloc(sizeof(int) * size);
*returnSize = size;
int i = 0;
//对于这种返回值不好处理的递归问题，我们可以设置子函数来解决
_preorderTraversal(root, retArr, &i);
return retArr;
}ps：这里也有个设计递归代码的常用小技巧，就是遇到函数返回值不好处理的情况下（比如这里要返回的int*，递归时并不好接收），我们可以写一个子函数并处理这里的返回值即可。
4.7 二叉树的中序遍历
int TreeSize(struct TreeNode* root)
{
return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
void _inorderTraversal(struct TreeNode* root, int* arr, int* pi)
{
if(!root)
return;
_inorderTraversal(root->left, arr, pi);
arr[(*pi)++] = root->val;
_inorderTraversal(root->right, arr, pi);
}
int* inorderTraversal(struct TreeNode* root, int* returnSize)
{
int size = TreeSize(root);
int* retArr = (int*)malloc(sizeof(int) * size);
*returnSize = size;
int i = 0;
_inorderTraversal(root, retArr, &i);
return retArr;
}4.8 二叉树的后序遍历
int TreeSize(struct TreeNode* root)
{
return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
void _postorderTraversal(struct TreeNode* root, int* arr, int* pi)
{
if(!root)
return;
_postorderTraversal(root->left, arr, pi);
_postorderTraversal(root->right, arr, pi);
arr[(*pi)++] = root->val;
}
int* postorderTraversal(struct TreeNode* root, int* returnSize)
{
int size = TreeSize(root);
int* retArr = (int*)malloc(sizeof(int) * size);
*returnSize = size;
int i = 0;
_postorderTraversal(root, retArr, &i);
return retArr;
}4.9 二叉树的创建
一串先序遍历字符串，根据此字符串建立一个二叉树。这题和上一题的前序遍历很相似，一个根据已有二叉树返回前序遍历的数组，一个根据前序遍历字符串来创建二叉树，所以这两道题有一个共同点，就是对数组下标的标识变量i的理解。
BTNode* BTreeCreate(char* str, int* pi)
{
if(str[*pi] == '#')
{
(*pi)++;
return NULL;
}
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
node->data = str[(*pi)++];//++优先级 > *优先级
node->left = BTreeCreate(str, pi);
node->right = BTreeCreate(str, pi);
return node;
}
void Inorder(BTNode* root)
{
if(!root)
return;
Inorder(root->left);
printf("%c ", root->data);
Inorder(root->right);
}
int main()
{
char str[100];
scanf("%s", str);
int i = 0;
BTNode* ret = BTreeCreate(str, &i);
Inorder(ret);
return 0;
}代码注意：
++运算符的优先级 > *运算符的优先级， *pi++会先对指针进行++，再解引用，导致代码出错，所以要加括号： （ *pi）++。
判断#的if语句部分不能（ *pi）++，要在if语句的代码块里面++，否则只要判断就会++。就算不是‘#’，i也会被++。
if(str[(*pi)++] == '#')//如果str[*pi]不为'#'，i也被++了。
return NULL;