数据结构与算法--八大排序
目录
1.基本概念:
1.排序:
2.需要掌握的点:
3.稳定性:
4.排序难点:
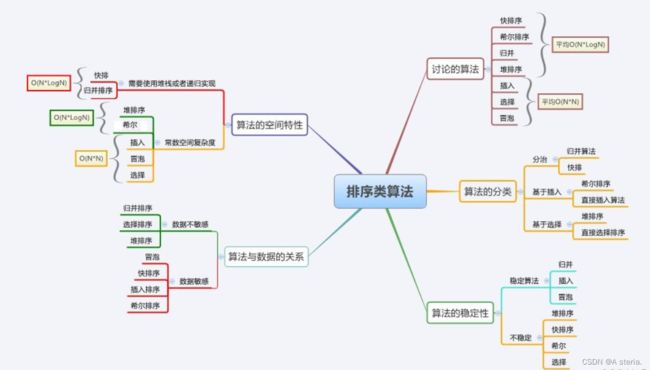
2.分类:
3.比较:
1.稳定性:
2.时间复杂度:
3.空间复杂度:
4.排序详解:
1.选择排序--直接插入排序
1.基本思想:
2.代码实现:
3.小结:
2.插入排序--希尔排序(Insert Sort)
1.基本思想:
2.实现方法:
3.算法实现:
4.代码实现:
5.小结:
3.选择排序-简单选择排序(Simple selection sort)
1.基本思想:
2.实现方法:
3.代码实现:
4.小结:
4.选择排序-堆排序(Heap sort)
1.基本思想:
2.实现方法:
3.算法实现:
4.代码实现:
5.小结:
5.交换排序-冒泡排序(Bubble Sort)
1.基本思想:
2.代码实现:
3.小结:
6.交换排序-快速排序(Quick-Sort)
1.基本思想:
2.代码实现:
3.小结:
7.归并排序-(Merge sort)
1.基本思想:
2.代码实现
3.小结:
8. 基数排序(Radix Sort)
1.基本思想:
2.代码实现:
3.小结:
5.总结:
1.基本概念:
1.排序:
把无序的数据变得有序,默认升序.笔试面试排名第一的内容
2.需要掌握的点:
1.算法描述;2.能实现;3.时间复杂度,空间复杂度以及稳定性;4.优缺点
3.稳定性:
对于关键字一样的数据假如A和A',在排序前A在A'的前面,排序后如果能保证A还在A'的前面那么这个算法稳定,否则不稳定
注意:稳定性是针对算法,不针对一次具体的实现.
判断稳定性简单的方法:是否有跳跃的交换数据,如果有则不稳定,没有则稳定
4.排序难点:
算法多,容易混淆
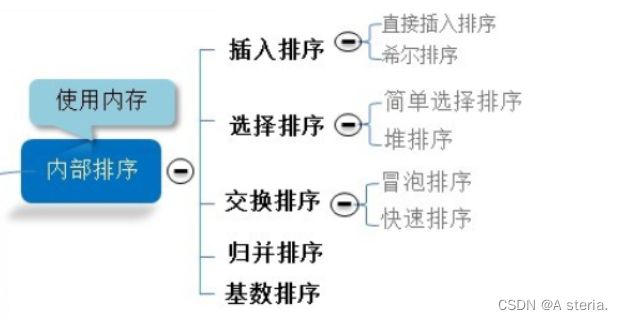
2.分类:
排序,而外部排序是因排序的数据很大,一次不能容纳全部的排序记录,在排序过程中需要访问外存。
3.比较:
1.稳定性:
稳定:直接插入排序;冒泡排序;归并排序;基数排序
不稳定:希尔排序;直接选择排序;堆排序;快速排序
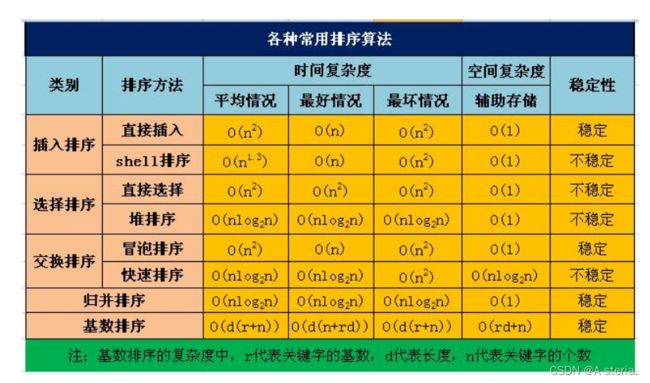
2.时间复杂度:
如下表:
3.空间复杂度:
O(1):直接插入排序;冒泡排序;归并排序;希尔排序;直接选择排序;堆排序;
4.排序详解:
1.选择排序--直接插入排序
1.基本思想:
在一个有序数组里面h2插入一个数据X,通过遍历比较找到位置,再把后面数据向后移动,把X插入到数组中,数组元素加一(插入单个数据);(对数组进行排序),设立一个临时变量存储作为临时存储和判断数组边界之用,将序列第一个元素当成是有序的,然后从第2个记录逐个进行插入,直至整个序列有序为止。![]()
相当于扑克牌
从当前位置开始, 从后往前找比当前数字小的, 找到后插入到这个小的数字后面;
在找的过程中, 如果发现一个比当前数字大, 同时将这个数字往后挪;
如果碰见一个和插入元素相等的,那么插入元素把想插入的元素放在相等元素的后面。所以,相等元素的前后顺序没有改变,从原无序序列出去的顺序就是排好序后的顺序,所以插入排序是稳定的。
2.代码实现:
void InsertSort(int* arr, int len)
{
int tmp;
int j;
for (int i = 1; i < len; i++)
{
tmp = arr[i];
for (j = i - 1; j >= 0; j--)
{
if (arr[j] > tmp)
arr[j + 1] = arr[j];
else
break;
}
arr[j + 1] = tmp;
}
}
void Show(int* arr, int len)
{
for (int i = 0; i < len; i++)
{
printf("%d ", arr[i]);
}
printf("\n");
}
int main()
{
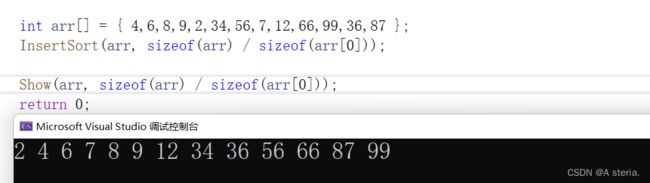
int arr[] = {4,6,8,9,2,34,56,7,12,66,99,36,87};
InsertSort(arr,sizeof(arr)/sizeof(arr[0]));
Show(arr, sizeof(arr) / sizeof(arr[0]));
return 0;
}void InsertSort(int* arr, int len)//O(n^2),最好的情况,O(1),
int tmp;//存放当前处理的数字
int j;//比较数字
for (int i = 1; i < len; i++)//从第二个数字开始
for (j = i - 1; j >= 0; j--)//从后往前找第一个比tmp小的数字
if (arr[j] > tmp)//arr[j]需要后移
arr[j + 1] = arr[j];
else break;//比当前最大的都大则不需要移动
arr[j + 1] = tmp;//直接放在最后
3.小结:
1. 元素集合越接近有序,直接插入排序算法的时间效率越高
2.时间复杂度:O(n ^ 2)(情况最差时, 即逆序转有序, 最好为O(n));
3.空间复杂度:O(1);
4.稳定
2.插入排序--希尔排序(Insert Sort)
1.基本思想:
先将整个数组分成若干个子数组,通过对子数组进行排序,达到数组"基本有序",再对整个数组进行插入排序,即可达到有序.
2.实现方法:
1.先分组,间隔为Gap的数据为一组,然后对这组数据进行排序,再分组,再排,直到数组被分完.
2.然后再把Gap减小,继续分组,排序.
3.此时数组基本有序,然后将最后Gap设为1,即进行直接插入排序,得到有序数组
![]()
3.算法实现:
先简单处理增量序列:增量序列gap=(gap/3+1),gap为要排序的数组数据个数。即:先将要排序的一组记录按某个增量gap(gap/3,gap为要排序数的个数)分成若干组子序列,每组中记录的下标相差gap/3.对每组中全部元素进行直接插入排序,然后再用一个较小的增量(gap/3)对它进行分组,在每组中再进行直接插入排序。继续不断缩小增量直至为1,最后使用直接插入排序完成排序。
希尔排序可以认为是插入排序的优化。
4.代码实现:
void Shell(int* arr, int len, int gap)
{
int tmp;
int j;
for (int i = gap; i < len; i++)
{
tmp = arr[i];
for (j = i - gap; j >= 0; j -= gap)
{
if (arr[j] > tmp)
arr[j + gap] = arr[j];
else
break;
}
arr[j + gap] = tmp;
}
}
void ShellSort(int* arr, int len)//O(n^1.3~n^1.5),O(1),不稳定
{
int d[] = { 5,3,1 };
for (int i = 0; i < sizeof(d) / sizeof(d[0]); i++)
{
Shell(arr, len, d[i]);
}
}
void Show(int* arr, int len)
{
for (int i = 0; i < len; i++)
{
printf("%d ", arr[i]);
}
printf("\n");
}
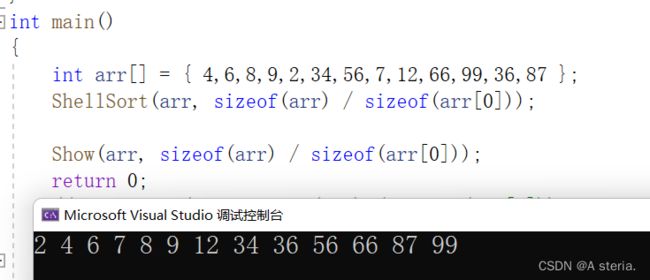
int main()
{
int arr[] = { 4,6,8,9,2,34,56,7,12,66,99,36,87 };
ShellSort(arr, sizeof(arr) / sizeof(arr[0]));
Show(arr, sizeof(arr) / sizeof(arr[0]));
return 0;
}void Shell(int* arr, int len, int gap)//gap:分组数
void ShellSort(int* arr, int len)//O(n^1.3~n^1.5),O(1),不稳定
int d[] = { 5,3,1 };//分组组数,注意最后一定是1.缩小增量
5.小结:
1. 希尔排序是对直接插入排序的优化。
2. 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。
3. 希尔排序的时间复杂度不好计算,需要进行推导,推导出来平均时间复杂度: O(N^1.3—N^2)
4. 稳定性:不稳定
3.选择排序-简单选择排序(Simple selection sort)
1.基本思想:
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完。
2.实现方法:
1.在数组[0,n]中选取最小的数,
2.交换数据,最小数放在左边,
3.在[1,n-1]再次选取,交换,缩减,直到集合剩一个元素
![]()
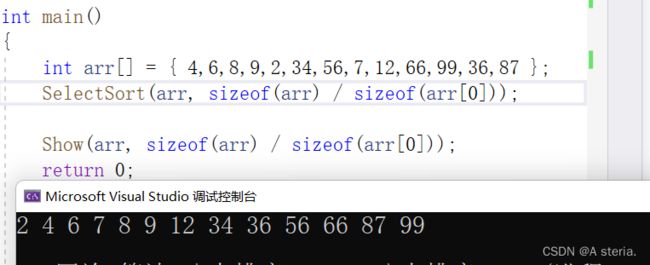
3.代码实现:
void SelectSort(int* arr, int len)
{
int minIndex;
int tmp;
for (int i = 0; i < len - 1; i++)
{
minIndex = i;
for (int j = i + 1; j < len; j++)
{
if (arr[minIndex] > arr[j])
{
minIndex = j;
}
}
if (minIndex != i)
{
tmp = arr[minIndex];
arr[minIndex] = arr[i];
arr[i] = tmp;
}
}
}
void Show(int* arr, int len)
{
for (int i = 0; i < len; i++)
{
printf("%d ", arr[i]);
}
printf("\n");
}
}
int main()
{
int arr[] = { 4,6,8,9,2,34,56,7,12,66,99,36,87 };
SelectSort(arr, sizeof(arr) / sizeof(arr[0]));
Show(arr, sizeof(arr) / sizeof(arr[0]));
return 0;
}void SelectSort(int* arr, int len)//O(n^2),O(1),不稳定
int minIndex;//最小值的下标;
for (int j = i + 1; j < len; j++)//找最小值
//最小值和待排序的第一个值交换
if (minIndex != i)
{
tmp = arr[minIndex];
arr[minIndex] = arr[i];
arr[i] = tmp;
}
4.小结:
1.容易理解,但是效率太低,实际当中不太使用
2.时间复杂度O(n^2),空间复杂度O(1);
3.不稳定
4.选择排序-堆排序(Heap sort)
1.基本思想:
堆排序(HeaoSort)是基于数据结构堆设计的一种排序算法,通过堆来选择数据,向上(向下)调整,得到小数(大数),然后再与堆底数据进行交换,即可排序,需要注意的是排升序建大堆,排降序建小堆
2.实现方法:
初始时把要排序的n个数的序列看作是一棵顺序存储的二叉树(一维数组存储二叉树),调整它们的存储序,使之成为一个堆,将堆顶元素输出,得到n 个元素中最小(或最大)的元素,这时堆的根节点的数最小(或者最大)。然后对前面(n-1)个元素重新调整使之成为堆,输出堆顶元素,得到n 个元素中次小(或次大)的元素。依此类推,直到只有两个节点的堆,并对它们作交换,最后得到有n个节点的有序序列。称这个过程为堆排序。
3.算法实现:
1. 建大堆, 把根交换到最底, 然后在减一个元素继续调整
2. 向下调整, 继续交换, 直到最后一个元素
4.代码实现:
void HeapAdjust(int* arr, int start, int end)//O(logn)
{
int tmp = arr[start];
for (int i = 2 * start + 1; i <= end; i = 2 * i + 1)
{
if (i < end && arr[i] < arr[i + 1])//有右孩子,并且左孩子的值小于右孩子
{
i++;
}//i一定是左右孩子的最大值
if (arr[i] > tmp)
{
arr[start] = arr[i];
start = i;
}
else
{
break;
}
}
arr[start] = tmp;
}
void HeapSort(int* arr, int len)//O(nlogn),O(1),不稳定
{
//第一次建立大根堆,从后往前,多次调整
int i;
for (i = (len - 1 - 1) / 2; i >= 0; i--)//从最后一棵子树开始,O(nlogn)
{
HeapAdjust(arr, i, len - 1);
}
//每次将根和待排序的最后一个交换,然后再调整
int tmp;
for (i = 0; i < len - 1; i++)//O(nlogn)
{
tmp = arr[0];
arr[0] = arr[len - 1 - i];
arr[len - 1 - i] = tmp;
HeapAdjust(arr, 0, len - 1 - i - 1);
}
}
void Show(int* arr, int len)
{
for (int i = 0; i < len; i++)
{
printf("%d ", arr[i]);
}
printf("\n");
}
int main()
{
int arr[] = { 4,6,8,9,2,34,56,7,12,66,99,36,87 };
HeapSort(arr, sizeof(arr) / sizeof(arr[0]));
Show(arr, sizeof(arr) / sizeof(arr[0]));
return 0;
}父--->子:i--->2*i+1,2*i+2;
子--->父:i---->(i-1)/2if (i < end && arr[i] < arr[i + 1])//有右孩子,并且左孩子的值小于右孩子
5.小结:
1.堆排序用来选数,效率就高了很多
2.时间复杂度O(n*logn),空间复杂度O(1);
3.不稳定
5.交换排序-冒泡排序(Bubble Sort)
1.基本思想:
在要排序的一组数中,对当前还未排好序的范围内的全部数,自上而下对相邻的两个数依次进行比较和调整,让较大的数往下沉,较小的往上冒。即:每当两相邻的数比较后发现它们的排序与排序要求相反时,就将它们互换。
![]()
2.代码实现:
void BubbleSort(int* arr, int len)
{
int tmp;
for (int i = 0; i < len - 1; i++)
{
for (int j = 0; j + 1 < len - i; j++)
{
if (arr[j] > arr[j + 1])
{
tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
}
}
}
}
void Show(int* arr, int len)
{
for (int i = 0; i < len; i++)
{
printf("%d ", arr[i]);
}
printf("\n");
}
int main()
{
int arr[] = { 4,6,8,9,2,34,56,7,12,66,99,36,87 };
BubbleSort(arr, sizeof(arr) / sizeof(arr[0]));
Show(arr, sizeof(arr) / sizeof(arr[0]));
return 0;
}void BubbleSort(int* arr, int len)//O(n^2),O(1),稳定
for (int i = 0; i < len - 1; i++)//趟数
3.小结:
1.容易理解
2.时间复杂度O(n^2),空间复杂度O(1)
3.稳定
6.交换排序-快速排序(Quick-Sort)
1.基本思想:
任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止,类似于树形结构,每次排序把Key值放到应在的位置.
将区间按照基准值划分为左右两半部分的常见方式有:
1. hoare版本:
Hoare版本(左右指针)
左边值设为key,然后右边先走,找小的,比key小,然后左边走找比key大,然后交换左边右边,
2. 挖坑法:
其设定key数组第一个值为坑,右边找下,左边找大,找到一个,交换,形成新的坑,最后把key放到坑里。
3. 前后指针版本
选取key值,cur小于key值,prev++,交换cur与prev值,
2.代码实现:
1. hoare版本:
int Partition(int* arr, int low, int high)//O(n),O(1)
{
int tmp = arr[low];//基准
while (low < high)
{
//从后往前找比基准小的数字,往前移动
while (low tmp)
{
high--;
}
if (low < high)
{
arr[low] = arr[high];
}
//从前往后找比基准大的数据,往后移动
while (low < high && arr[low] <= tmp)
{
low++;
}
if (low < high)
{
arr[high] = arr[low];
}
}
arr[low] = tmp;
return low;
}
void Quick(int* arr, int low, int high)//O(nlogn),O(logn),不稳定
{
int par = Partition(arr, low, high);
if (low < par - 1)//左边数据超过一个
{
Quick(arr, low, par - 1);
}
if (par + 1 < high)
{
Quick(arr, par + 1, high);
}
}
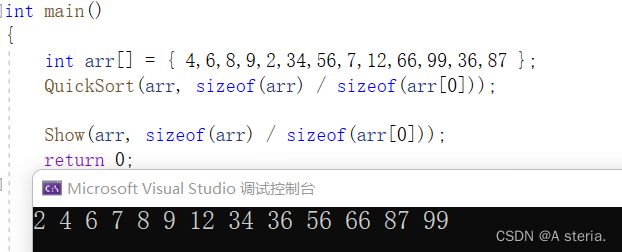
void QuickSort(int* arr, int len)
{
Quick(arr, 0, len - 1);
}
void Show(int* arr, int len)
{
for (int i = 0; i < len; i++)
{
printf("%d ", arr[i]);
}
printf("\n");
}
int main()
{
int arr[] = { 4,6,8,9,2,34,56,7,12,66,99,36,87 };
QuickSort(arr, sizeof(arr) / sizeof(arr[0]));
Show(arr, sizeof(arr) / sizeof(arr[0]));
return 0;
} 2.挖坑法:
int PartSort2(int* a, int left, int right)
{
int key = a[left];
while (left < right)
{
//找小的
while (left < right && a[right] >= key)
{
--right;
}
a[left] = a[right];//找到小值,放到坑里,形成新的坑
while (left < right && a[left] <= key)
{
++left;
}
a[right] = a[left];//找到大值,放到坑里,形成新的坑
}
a[left] = key;//把key放到数组中属于它的位置,左边所有值小于它,右边所有值大于它,
return left; //返回left,分组处理数据
}
void QuickSort(int* a, int left, int right)//快排
{
if (left >= right)
{
return;
}
int key = PartSort2(a, left, right);
// [begin, keyi-1] keyi [keyi+1, end]
//类似于二叉树
QuickSort(a, left, key - 1);//递归对左数组排序
QuickSort(a, key + 1, right);//递归对右数组排序
}
void Show(int* arr, int len)
{
for (int i = 0; i < len; i++)
{
printf("%d ", arr[i]);
}
printf("\n");
}
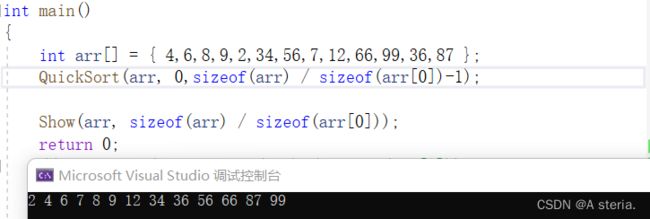
int main()
{
int arr[] = { 4,6,8,9,2,34,56,7,12,66,99,36,87 };
QuickSort(arr, 0,sizeof(arr) / sizeof(arr[0])-1);
Show(arr, sizeof(arr) / sizeof(arr[0]));
return 0;
}
3.前后指针法
#include
#include
using namespace std;
int PartSort3(int* a, int left, int right)
{
int keyi = left;
int cur = left + 1;
int prev = left;
while (cur <= right)
{
if (a[cur] < a[keyi] && ++prev != cur)//判断cur与key的值,并且防止自己与自己交换
{
swap(&a[cur], &a[prev]);
}
++cur;
}
swap(&a[keyi], &a[prev]);
return prev;
}
void QuickSort(int* a, int left, int right)//快排
{
if (left >= right)
{
return;
}
int key = PartSort3(a, left, right);
// [begin, keyi-1] keyi [keyi+1, end]
//类似于二叉树
QuickSort(a, left, key - 1);//递归对左数组排序
QuickSort(a, key + 1, right);//递归对右数组排序
}
3.小结:
1.快速排序整体的综合性能和使用场景都是比较好的
2.时间复杂度:O(N*logN)
3.空间复杂度:O(N*logN
4.不稳定
7.归并排序-(Merge sort)
1.基本思想:
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide andConquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。通过递归实现对小数组有序,再返回回来。
2.代码实现:
static void Merge(int* arr, int len, int gap)//O(n)
{
int low1 = 0;//第一个归并段的起始下标;
int high1 = low1 + gap - 1;//第一个归并段的结束下标;
int low2 = high1 + 1;//第二个归并段的起始下标;
int high2 = low2 + gap < len ? low2 + gap - 1 : len - 1;
int* brr = (int*)malloc(len * sizeof(int));//存放归并好的数据;
int i = 0;//brr的下标;
assert(brr != NULL);
//1.有两个归并段
while (low2 < len)
{
//两个归并段都还有数据,需要比
while (low1 <= high1 && low2 <= high2)
{
if (arr[low1] <= arr[low2])
{
brr[i++] = arr[low1++];
}
else
{
brr[i++] = arr[low2++];
}
}
//一个归并段的数据已经完成了,另一个还有数据
while (low1 <= high1)
{
brr[i++] = arr[low1++];
}
while (low2 <= high2)
{
brr[i++] = arr[low2++];
}
//下两个归并段
low1 = high2 + 1;
high1 = low1 + gap - 1;
low2 = high1 + 1;
high2 = low2 + gap < len ? low2 + gap - 1 : len - 1;
}
//2.只有一个归并段
while (low1 < len)
{
brr[i++] = arr[low1++];
}
//3.将归并好的数据拷贝到arr中
for (i = 0; i < len; i++)
{
arr[i] = brr[i];
}
free(brr);//不要忘记
}
void MergeSort(int* arr, int len)//O(nlogn),O(n),稳定
{
for (int i = 1; i < len; i *= 2)//O(log n )
{
Merge(arr, len, i);
}
}
void Show(int* arr, int len)
{
for (int i = 0; i < len; i++)
{
printf("%d ", arr[i]);
}
printf("\n");
}
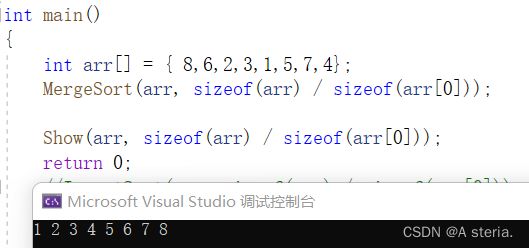
int main()
{
int arr[] = { 8,6,2,3,1,5,7,4};
MergeSort(arr, sizeof(arr) / sizeof(arr[0]));
Show(arr, sizeof(arr) / sizeof(arr[0]));
return 0;
}3.小结:
1. 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
2. 时间复杂度:O(N*logN)
3. 空间复杂度:O(N)
4. 稳定性:稳定
8. 基数排序(Radix Sort)
1.基本思想:
1. 统计相同元素出现次数
2. 根据统计的结果将序列回收到原来的序列中
![]()
2.代码实现:
sort.cpp
#include
#include
#include
#include "listqueue.h"
void RadixSort(int* arr, int len)//O(d*n),O(n),稳定
{
//需要10个链式队列,存放进队的数字
LinkQueue queArr[10];//定义了10个队头;
for (int i = 0; i < 10; i++)
{
InitQueue(&queArr[i]);
}
//得到最大数字的位数,确定进队和出队的次数
int count = GetFigur(arr, len);
int index;//队列的下标
for (int i = 0; i < count; i++)//两个含义:1.次数;2.处理每个数字从右往左的第i个数字
{
for (int j = 0; j < len; j++)//遍历数组并入队
{
index = GetNum(arr[j], i);//index保存arr[j]应该进入对的队列下标
//获取十进制整数右数第i位的数字
Push(&queArr[index], arr[j]);//将数字存放的对应的队列;
}
//出队
int j = 0;
for (int k = 0; k < 10; k++)
{
while (!IsEmpty(&queArr[k]))
{
DeQueue(&queArr[k], &arr[j++]);
}
}
//销毁
for (int i = 0; i < 10; i++)
{
Destroy(&queArr[i]);
}
}
}
void Show(int* arr, int len)
{
for (int i = 0; i < len; i++)
{
printf("%d ", arr[i]);
}
printf("\n");
}
int main()
{
int arr[] = { 8,6,2,3,1,5,7,4};
RadixSort(arr, sizeof(arr) / sizeof(arr[0]));
Show(arr, sizeof(arr) / sizeof(arr[0]));
return 0;
} listqueue.h
#pragma once
//链式队列,队头在首元节点,队尾在尾节点
typedef int ElemType;
typedef struct QNode//数据节点
{
ElemType data;
struct QNode* next;
}QNode, * QueuePtr;
typedef struct
{
QNode* front;//队头指针
QNode* rear;//队尾指针
}LinkQueue;//头结点的定义
//队列初始化
void InitQueue(LinkQueue* pq);
//入队
bool Push(LinkQueue* pq, ElemType val);
//判空
bool IsEmpty(LinkQueue* pq);
//获取队头元素,但不删除
bool GetHead(LinkQueue* pq, ElemType* rtval);
//出队,获取队头元素,且删除
bool DeQueue(LinkQueue* ps, ElemType* rtval);
//销毁
void Destroy(LinkQueue* ps);listqueue.cpp
#pragma once
//链式队列,队头在首元节点,队尾在尾节点
typedef int ElemType;
typedef struct QNode//数据节点
{
ElemType data;
struct QNode* next;
}QNode, * QueuePtr;
typedef struct
{
QNode* front;//队头指针
QNode* rear;//队尾指针
}LinkQueue;//头结点的定义
//队列初始化
void InitQueue(LinkQueue* pq);
//入队
bool Push(LinkQueue* pq, ElemType val);
//判空
bool IsEmpty(LinkQueue* pq);
//获取队头元素,但不删除
bool GetHead(LinkQueue* pq, ElemType* rtval);
//出队,获取队头元素,且删除
bool DeQueue(LinkQueue* ps, ElemType* rtval);
//销毁
void Destroy(LinkQueue* ps);
3.小结:
1. 计数排序在数据范围集中时,效率很高,但是适用范围及场景有限。
2. 时间复杂度:O(MAX(N,范围))
3. 空间复杂度:O(范围)
4. 稳定性:稳定
5.总结: