【AcWing】AcWing 5170. 二进制（秋季每日一题2023）（并查集 + 逆元求组合数）

题目

https://www.acwing.com/problem/content/5173/

题目大意：给定 N,K以及一个 K-子串数字和序列，请你计算一共有多少个不同的长度为 N的二进制串可以得到该 K-子串数字和序列。（K-子串数字和序列参考题目中的定义）

思路

首先看数据范围，N和K都是$10^6$，所以复杂度要控制在$O(nlogn)$以内。下面是分析思路。

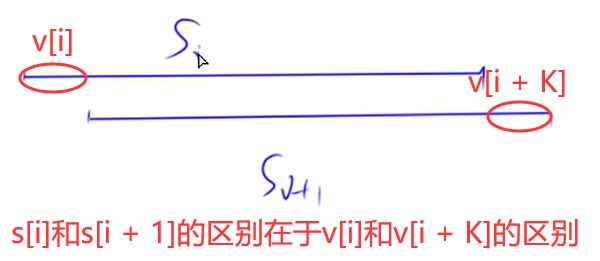
首先看K-子串数字和序列有什么特点。对于相邻的两个和来说，对应到原序列中，是重叠的两个区间，重叠部分长度为$K-1$，而两个区间的和的区别就在不重叠的两个数上。即假设第一个区间为$[i,i+K-1]$，第二个区间为$[i+1,i+k]$，原序列为$v[N]$，K-子串数字和序列为$s[N]$，则$s[i]$和$s[i+1]$的区别主要在于$v[i]$和$v[i+K]$的区别上。示意图如下：

根据这个特点，我们可以得到两个结论：

1. 根据$s[i]$和$s[i+1]$的关系，确定$v[i]$和$v[i+K]$的关系
2. 由于可以根据$[i,i+K-1]$推出$[i+1,i+K]$的值，所以只需要确定第一个区间$[0,K-1]$中的所有数，整个原始序列就确定了。即原始序列的方案数 = 第一个区间所有取值的方案数

第1个结论具体来说：

• 当$s[i]$和$s[i+1]$相同时，$v[i]$和$v[i+K]$相等
• 当$s[i]>s[i+1]$时，由于是二进制串，所以取值只有一种情况，$v[i]=1，v[i+K]=0$
• 当$s[i]<s[i+1]$时，$v[i]=0，v[i+K]=1$

下面只需要求出第1个区间的方案数有多少。根据第1个结论，第1个区间中有些数是可以根据后面的区间确定的，即确定为0或者是1。比如，假设$N=7，K=3$，K-子串数字和序列$2,2,2,2,3$，则

• 根据$s[0]=s[1]$，可以推出$v[0]=v[3]$
• 根据$s[3]=s[4]$，可以推出$v[3]=0，v[6]=1$，进而推出$v[0]=0$

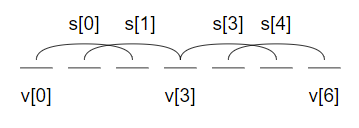
所以可以看出，对于相同的值，只要其中1个值确定了，所有的值就都确定了，示意图如下：

所以可以用并查集将相同的值存到一个集合中，每当集合中有一个值确定的时候，就将集合中的代表元素进行赋值。这样最终就可以得到第1个区间中有多少个0，多少个1，然后利用组合数$C_{K-c0-c1}^{s[0]-c1}$求方案数即可。由于数据范围是$10^6$，这是个大组合数，所以需要用逆元来求组合数。

最终算法如下：

1. 求第1个区间中有多少个0和1，分别记为$c0$个、$c1$个
   （1）. 先遍历所有的$s[i]$，判断$s[i]==s[i+1]$是否成立。如果成立，将$i和i+K$放入同一个集合中
   （2）. 再次遍历所有的$s[i]$，判断$s[i]!=s[i+1]$是否成立，并确定$v[i],v[i+K]$取值为0还是1
   （3）. 统计第1个区间中有多少个0和1
2. 利用逆元计算组合数$C_{K-c0-c1}^{s[0]-c1}$

时间复杂度

第1步，$O((N-K)\ast 1)+O((N-K)\ast 1)+O(K)=O(2\ast (N-K)+K)$，其中1表示并查集合并或者查找根节点的时间复杂度
第2步，$O(NlogN)$，其中N是求组合数的复杂度，logN是快速幂的复杂度。

所以总共为$O(NlogN+2\ast (N-K)+K)$

代码

#include 

typedef long long LL;

const int N = 1000010, MOD = 1e6 + 3;
int n, k;
int p[N]; // 并查集数组
int v[N], s[N]; // v[N]原序列每一位的值, s[N]子串数字和序列

using namespace std;

int find(int x) { // 并查集查找 + 路径压缩
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int qmi(int a, int b) { // 快速幂
    int res = 1;
    while (b) {
        if (b & 1) res = (LL)res * a % MOD;
        a = (LL)a * a % MOD;
        b >>= 1;
    }
    return res;
}

int C(int a, int b) {  // 求组合数
    int fa = 1, fb = 1, fab = 1;
    for(int i = 1; i <= a; i ++ ) fa = (LL)fa * i % MOD;
    for(int i = 1; i <= b; i ++ ) fb = (LL)fb * i % MOD;
    for(int i = 1 ; i <= a - b; i ++ ) fab = (LL)fab * i % MOD;
    
    return (LL)fa * qmi(fb, MOD - 2) * qmi(fab, MOD - 2) % MOD;
}

int main() {
    scanf("%d%d", &n, &k);
    for(int i = 0; i < n - k + 1; i ++ ) scanf("%d", &s[i]);
    
    // v数组第1个区间有多少个0和1
    for(int i = 0; i < n; i ++ ) v[i] = -1; // 初始化：v[N]，-1表示数字未确定；0和1表示已确定
    for(int i = 0; i < n; i ++ ) p[i] = i; // 初始化：p[N]，并查集数组
    
    for(int i = 0, j = k; i < n - k; i ++, j ++ ) { // 遍历所有的s[i]，确定v[i]和v[i + k]的关系，将相同的值放入同一个集合
        if (s[i] == s[i + 1]) p[find(j)] = find(i);
    }
    for(int i = 0, j = k; i < n - k; i ++, j ++ ) { // 再次遍历所有的s[i]，如果s[i] != s[i + 1]，确定集合值等于0还是1
        if (s[i] > s[i + 1]) v[find(i)] = 1, v[find(j)] = 0; 
        else if (s[i] < s[i + 1]) v[find(i)] = 0, v[find(j)] = 1;
    }
    
    int c0 = 0, c1 = 0;
    for(int i = 0; i < k; i ++ ) {
        if (v[find(i)] == 1) c1 ++ ;
        else if (v[find(i)] == 0) c0 ++ ;
    } // 注意：为了保险起见，这里要写v[find(i)]，不要写成v[i]。因为存在这种情况：前面合并集合的时候，写的是p[find(i)] = find(j)，那么j就是祖先节点了
      // 这样在后面赋值0、1的时候，由于是给集合的根节点赋值，所以就是给j赋值的，这个时候v[i]还是没有值的，v[find(i)]才有值。
    
    // 计算组合数
    printf("%d", C(k - c0 - c1, s[0] - c1));  
    
    return 0;
}

总结

• 对于有相同属性的元素，可以用并查集将他们放在同一个集合中，这样更新节点属性的时候，只需要更新集合代表元素的属性即可。使用了路径压缩的并查集的时间复杂度近乎$O(1)$
• 求组合数的方法有很多种，对于不同的数据范围，使用不同的方法