【Transformer系列】深入浅出理解Attention和Self-Attention机制
一、参考资料
论文:Attention Is All You Need
课件:10_Transformer_1.pdf
视频:Transformer模型(1/2): 剥离RNN,保留Attention
二、Attention without RNN
Attention模型可以看到全局的信息。
本章节以 Seq2Seq( (encoder + decoder)) 模型为例,介绍Attention机制。
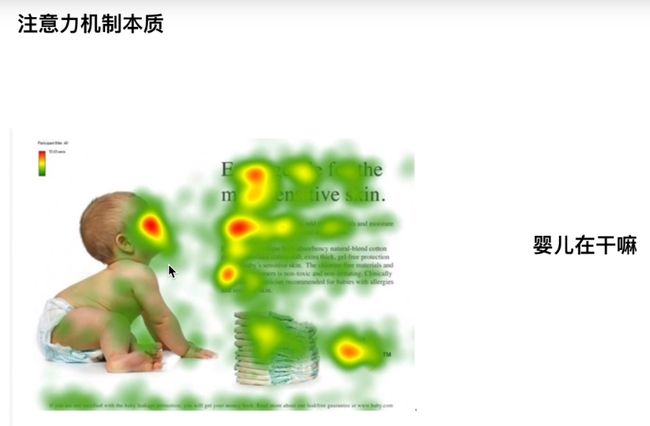
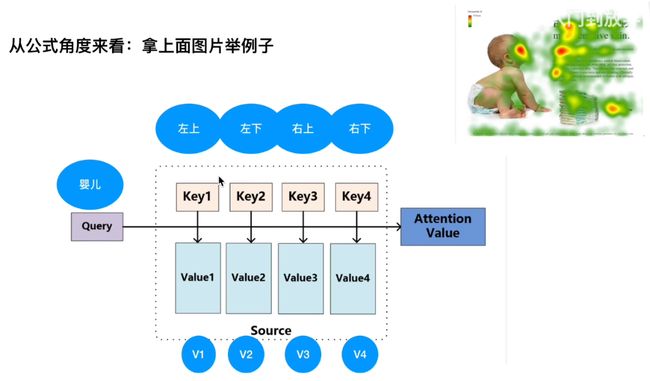
0. Attention直观理解
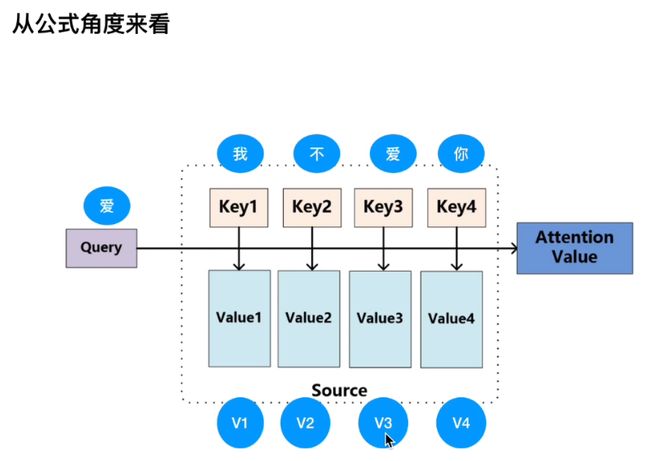
1. Keys&Values&Query定义
Q 矩阵来自decoder模块,K/V矩阵来自encoder。
-
Encoder’s inputs are vectors x 1 , x 2 , ⋯ , x m \mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_m x1,x2,⋯,xm.
-
Decoder’s inputs are vectors x 1 ′ , x 2 ′ , ⋯ , x t ′ \color{red}{\mathbf{x}_1^{\prime}},\color{red}{\mathbf{x}_2^{\prime}},\cdots,\color{red}{\mathbf{x}_t^{\prime}} x1′,x2′,⋯,xt′.

-
K e y s \color{red}{Keys} Keys and V a l u e s \color {red}{Values} Values are based on encoder’s inputs x 1 , x 2 , ⋯ , x m \mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_m x1,x2,⋯,xm.
-
Q u e r i e s \color {red}{Queries} Queries are based on decoder’s inputs x 1 ′ , x 2 ′ , ⋯ , x t ′ \color{red}{\mathbf{x}_1^{\prime}},\color{red}{\mathbf{x}_2^{\prime}},\cdots,\color{red}{\mathbf{x}_t^{\prime}} x1′,x2′,⋯,xt′.
-
K e y s \color{red}{Keys} Keys: k : i = W K x i \mathbf{k}_{:i}=\mathbf{W}_K\mathbf{x}_i k:i=WKxi.
-
V a l u e s \color {red}{Values} Values: v : i = W V x i \mathbf{v}_{:i}=\mathbf{W}_V\mathbf{x}_i v:i=WVxi.
-
Q u e r y \color {red}{Query} Query: q : j = W Q x j ′ {\mathbf{q}_{:j}=\mathbf{W}_Q}{\mathbf{x}_j^{\prime}} q:j=WQxj′.


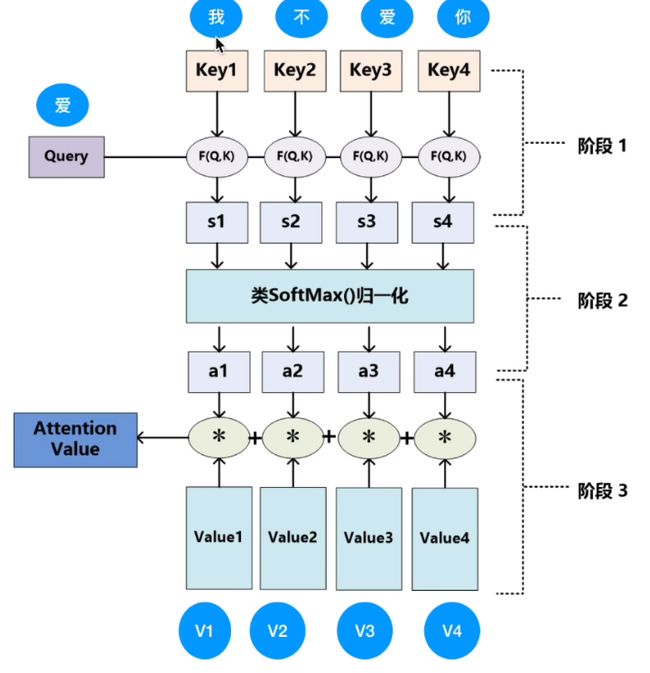
2. Attention机制的原理
2.1 Compute weights
α : 1 = S o f t m a x ( K T q : 1 ) ∈ R m {\alpha_{:1}=\mathrm{Softmax}(\mathbb{K}^T{q_{:1}})\in\mathbb{R}^m} α:1=Softmax(KTq:1)∈Rm
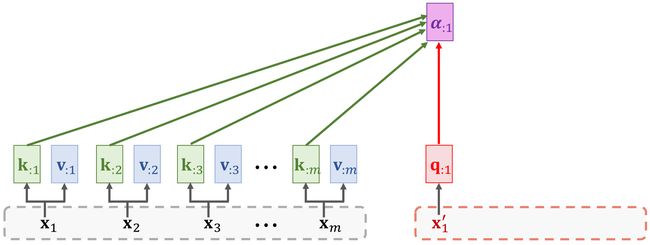
α : 2 = S o f t m a x ( K T q : 2 ) ∈ R m {\alpha_{:2}=\mathrm{Softmax}(\mathbb{K}^T{q_{:2}})\in\mathbb{R}^m} α:2=Softmax(KTq:2)∈Rm
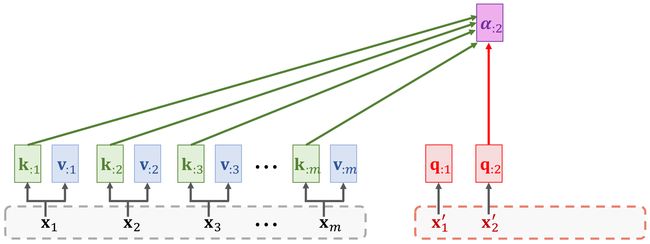
2.2 Compute context vector
c : 1 = α : 1 v : 1 + ⋯ + α : m v : m = V α : 1 {\mathbf{c}_{:1}=\alpha_{:1}\mathbf{v}_{:1}+\cdots+\alpha_{:m}\mathbf{v}_{:m}=\mathbf{V}\mathbf{\alpha}_{:1}} c:1=α:1v:1+⋯+α:mv:m=Vα:1

c : 2 = α 12 v : 1 + ⋯ + α : m v : m = V α : 2 {c_{:2}=\alpha_{12}v_{:1}+\cdots+\alpha_{:m}v_{:m}=V\alpha_{:2}} c:2=α12v:1+⋯+α:mv:m=Vα:2
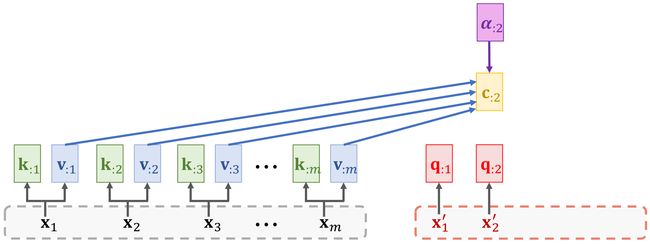
c : j = α 1 j v : 1 + ⋯ + α m j v : m = V α : j {\mathrm{c}_{:j}}=\alpha_{1j}\mathbf{v}_{:1}+\cdots+\alpha_{mj}\mathbf{v}_{:m}=\mathbf{V}\mathbf{\alpha}_{:j} c:j=α1jv:1+⋯+αmjv:m=Vα:j

2.3 Output of attention layer
-
C = [ c : 1 , c : 2 , c : 3 , ⋯ , c : t ] {C=[c_{:1},c_{:2},c_{:3},\cdots,c_{:t}]} C=[c:1,c:2,c:3,⋯,c:t].
-
c : j = V ⋅ S o f t m a x ( K T q : j ) {\mathrm{c}_{:j}=\mathrm{V}\cdot\mathrm{Softmax}(\mathrm{K}^T {\mathbf{q}_{:j}})} c:j=V⋅Softmax(KTq:j).
-
c : j \mathrm{c}_{:j} c:j is a function of X j ′ \mathbf{X}_j^{\prime} Xj′ and [ x 1 , ⋯ , x m ] [\mathbf{x}_1,\cdots,\mathbf{x}_m] [x1,⋯,xm].
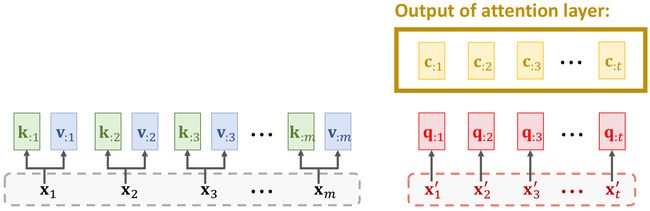
2.4 Attention Layer
- Attention layer: C = A t t n ( X , X ′ ) \mathrm{C}=\mathrm{Attn}(\mathbf{X},\mathbf{X}^{\prime}) C=Attn(X,X′).
- Encoder’s inputs: X = [ x 1 , x 2 , ⋯ , x m ] \mathbf{X}=[\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_m] X=[x1,x2,⋯,xm].
- Decoder’s inputs: X ′ = [ x 1 ′ , x 2 ′ , ⋯ , x t ′ ] \mathbf{X}^{\prime}=[x_1^{\prime},x_2^{\prime},\cdots,x_t^{\prime}] X′=[x1′,x2′,⋯,xt′].
- Parameters: W Q , W K , W V \mathbf{W}_Q\textbf{, W}_K\textbf{, W}_V WQ, WK, WV.

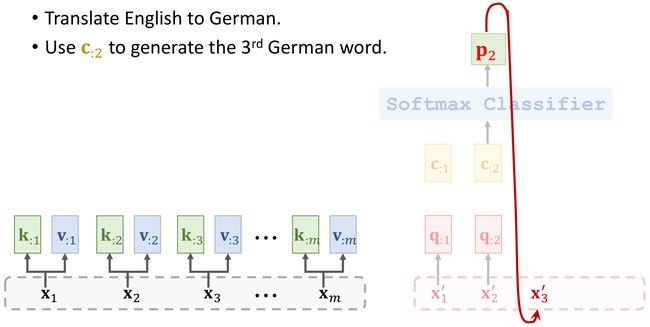
2.5 Machine Translation
本章节介绍Attention机制在Machine Translation机器翻译任务中的应用。将English翻译成German。

3. Attention最新研究
比标准Attention快197倍!Meta推出多头注意力机制“九头蛇”
Hydra Attention: Efficient Attention with Many Heads
三、Self-Attention without RNN
The Illustrated Transformer
Attention机制详解(二)——Self-Attention与Transformer
深度学习attention机制中的Q,K,V分别是从哪来的?
1. 引言
在介绍Self-Attention之前,先举了一个语义处理的例子:
“The animal didn’t cross the street because it was too tired.”
我们人很容易理解,后面的it是指animal,但是要怎么让机器能够把it和animal关联起来呢?如下图所示,我们应当有一个结构能够表达每个单词和其他每个单词的关系,Self-attention就是在这种需求下产生的。

Self-Attention机制,最先在NLP中提出,其核心是利用文本中的其他词来增强目标词特征的表征能力,从而得到一个聚焦重点的句子特征。
2. Self-Attention结构
Self-Attention 中文翻译为自注意力机制,论文中叫作 Scale Dot Product Attention,它是 Transformer 架构的核心,其结构如下图所示:

3. Self-Attention机制的原理
3.0 Keys&Values&Query定义
-
输入为 x 1 , x 2 , x 3 , . . , x m \color{red}{x_1, x_2, x_3,..,x_m} x1,x2,x3,..,xm。
-
Q u e r y \color{red}{Query} Query: q : i = W Q x i \mathbf{q}_{:i}=\mathbf{W}_Q\mathbf{x}_i q:i=WQxi;
-
K e y \color{red}{Key} Key: k : i = W K x i \mathbf{k}_{:i}=\mathbf{W}_K\mathbf{x}_i k:i=WKxi;
-
V a l u e \color{red}{Value} Value: v : i = W V x i \mathbf{v}_{:i}=\mathbf{W}_V\mathbf{x}_i v:i=WVxi;

3.1 Compute Weights
α : 1 = S o f t m a x ( K T q : 1 ) ∈ R m \alpha_{:1}=\mathrm{Softmax}(\mathbb{K}^T{q}_{:1})\in\mathbb{R}^m α:1=Softmax(KTq:1)∈Rm

α : 2 = S o f t m a x ( K T q : 2 ) ∈ R m \alpha_{:2}=\mathrm{Softmax}(\mathbb{K}^T\mathbf{q}_{:2})\in\mathbb{R}^m α:2=Softmax(KTq:2)∈Rm

α : j = S o f t m a x ( K T q : j ) ∈ R m \alpha_{:j}=\mathrm{Softmax}(\mathbb{K}^T\mathbf{q}_{:j})\in\mathbb{R}^m α:j=Softmax(KTq:j)∈Rm
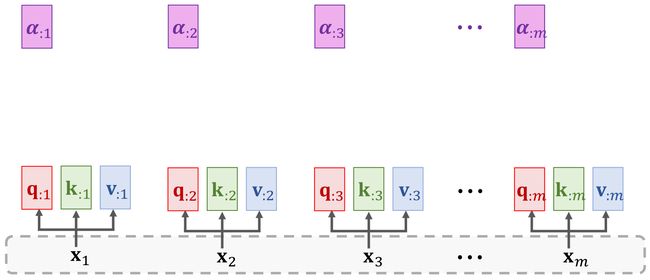
3.2 Compute Context vector
c : 1 = α 11 v : 1 + ⋯ + α m 1 v : m = V α : 1 \mathbf{c}_{:1}=\alpha_{11}\mathbf{v}_{:1}+\cdots+\alpha_{m1}\mathbf{v}_{:m}=\mathbf{V}\mathbf{\alpha}_{:1} c:1=α11v:1+⋯+αm1v:m=Vα:1
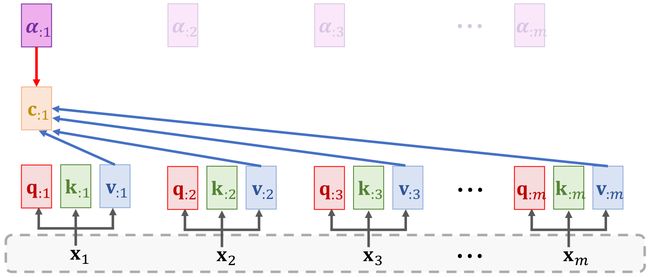
c : 2 = α 12 v : 1 + ⋯ + α m 2 v : m = V α : 2 c_{:2}=\alpha_{12}v_{:1}+\cdots+\alpha_{m2}v_{:m}=V\alpha_{:2} c:2=α12v:1+⋯+αm2v:m=Vα:2
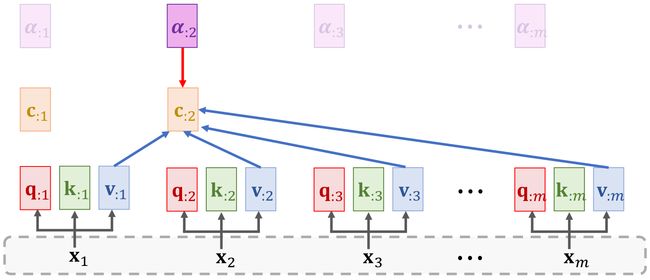
c : j = α 1 j v : 1 + ⋯ + α m j v : m = V α : j \mathrm{c}_{:j}=\alpha_{1j}\mathrm{v}_{:1}+\cdots+\alpha_{mj}\mathrm{v}_{:m}=\mathrm{V}\alpha_{:j} c:j=α1jv:1+⋯+αmjv:m=Vα:j

3.3 Output of Self-Attention layer
- c : j = V ⋅ S o f t m a x ( K T q : j ) \mathrm{c}_{:j}=\mathrm{V}\cdot\mathrm{Softmax}(\mathbb{K}^T\mathbf{q}_{:j}) c:j=V⋅Softmax(KTq:j).
- c : j \mathrm{c}_{:j} c:j is a function of all the vectors x 1 , ⋯ , X m \mathbf{x}_1,\cdots,\mathbf{X}_m x1,⋯,Xm.

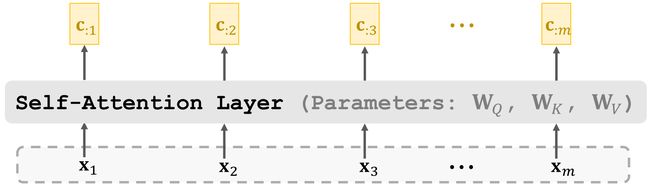
3.4 Self-Attention Layer
- Self-attention layer: C = A t t n ( X , X ) \mathrm{C}=\mathrm{Attn}(\mathbf{X},\mathbf{X}) C=Attn(X,X).
- Inputs: X = [ x 1 , x 2 , ⋯ , x m ] \mathbf{X}=[\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_m] X=[x1,x2,⋯,xm].
- Parameters: W Q , W K , W V \mathbf{W}_Q\textbf{, W}_K\textbf{, W}_V WQ, WK, WV.
4. Self-Attention的计算过程
4.0 先验知识
先验知识:向量点乘(内积)表征两个向量的夹角,表征一个向量在另一个向量上的投影,投影的值越大,说明两个向量相关度越高。如果两个向量夹角是九十度(垂直),那么这两个向量线性无关,完全没有相关性。
- a和b同向,则 a ∗ b = ∣ a ∣ ∣ b ∣ a*b=|a||b| a∗b=∣a∣∣b∣;
- 如果a和b垂直,则 a ∗ b = 0 a*b=0 a∗b=0;
- 如果a和b反向,则 a ∗ b = − ∣ a ∣ ∣ b ∣ a*b=-|a||b| a∗b=−∣a∣∣b∣。
所以,两个向量的点乘(点积)可以表示两个向量的相似度,越相似则方向越趋于一致,a点乘b数值越大。
4.1 主要步骤
输入序列单词的 Embedding Vector 经过线性变换(Linear 层)得到 Q、K、V 三个向量,并将它们作为 Self-Attention 层的输入。假设输入序列的长度为 seq_len,则 Q、K 和 V 的形状为[seq_len,d_k],其中, d k \text{d}_{\text{k}} dk 表示每个词或向量的维度,也是 Q、K 矩阵的列数。在论文中,输入给 Self-Attention 层的 Q、K、V 的向量维度是 64, Embedding Vector 和 Encoder-Decoder 模块输入输出的维度都是 512。
计算Thinking的Self-Attention,主要步骤有:
- 首先计算Q向量与K向量之间的点乘;
- 然后为了防止其结果过大,会除以一个尺度标度(缩放因子) d k \sqrt{d_{k}} dk,其中 d k d_{k} dk 为一个query和key向量的维度;
- 再利用Softmax操作其结果归一化为概率分布(注意力向量)。比如,[0.88, 0.12]这个向量的意思是,要解释Thinking这个词在这个句子中的意思,应当取0.88份Thinking原本的意思,再取0.12份Machine原本的意思,这样加权就是Thinking在这个句子中的意思;
- 然后乘以V向量,得到加权向量(权重求和的表示);
Self-Attention 层的计算过程用数学公式可表达为:
A t t e n t i o n ( Q , K , V ) = s o f t m a x ( Q K T d k ) V Attention(Q,K,V)=softmax(\frac{QK^{T}}{\sqrt{d_{k}}})V Attention(Q,K,V)=softmax(dkQKT)V
如果看代码就会发现,QKV仅仅是对X做了三次线性变换(三个不同的全连接层),然后得到了QKV三个X变换之后的输出。它们三个在计算的时候,任意指定一个为QKV都可以(当然,指定后就不能变了)。得到QKV之后, s o f t m a x ( Q K T d k ) V softmax(\frac{QK^{T}}{\sqrt{d_{k}}})V softmax(dkQKT)V 才是真正的计算注意力的过程。所谓QKV,不过是为了引入可训练的参数,同时对X进行特征空间变换。所以,我们关心得到的三个全连接层的参数矩阵就好了,不用给QKV多么直观的解释,QKV仅仅是线性变换。
4.2 举例说明
举例,我们要翻译一个词组 Thinking Machines,其中Thinking输入的Embedding vector用 X 1 X_1 X1 表示,Machines的Embedding vector用 X 2 X_2 X2 表示。在CV领域,Thinking和Machine可以理解为图片被切分的两个patch。

Step 1——
在Transformer论文中,Self-Attention会计算出三个新的向量,向量的维度是512维,我们把这三个向量分别称为Query、Key、Value。这三个向量是用embedding向量与一个权重矩阵相乘得到的结果,这个矩阵是随机初始化的,维度为(64,512),注意第二个维度需要和embedding的维度一样,其值在BP的过程中会一直进行更新,得到的这三个向量的维度是64。

Step 2——
当我们处理Thinking这个词时,我们需要计算句子中所有词与它的Self-Attention Score分数值,该分数值决定了当我们在某个位置encode一个词时,对输入句子的其他词的相关度(重要程度或关注程度)。简单理解,就是将当前词当作搜索的query,去和句子中所有词(包含该词本身)的key去匹配,看看相关度有多高。
W Q W^Q WQ 矩阵是 X 1 X_1 X1 的权重矩阵, q 1 = X 1 ∗ W Q q_1 = X1 * W^Q q1=X1∗WQ,所以我们用 q 1 q_1 q1 代表 Thinking 对应的 query vector, k 1 k_1 k1 及 k 2 k_2 k2 分别代表 Thinking以及Machines对应的 key vector,则计算 Thinking 的 Self-Attention Score的时候需要计算 q 1 q_1 q1 与 k 1 , k 2 k_1,k_2 k1,k2 的点乘,同理,我们计算Machines 的 Attention Score的时候需要计算 q 2 q_2 q2 与 k 1 , k 2 k_1,k_2 k1,k2 的点乘。如下图所示,我们分别得到 q 1 q_1 q1 与 k 1 , k 2 k_1,k_2 k1,k2 的点乘积。
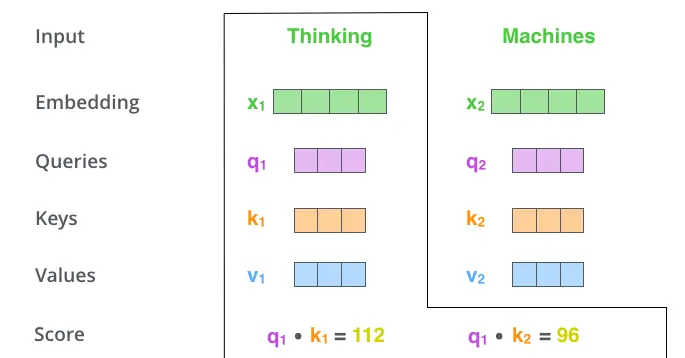
Step 3——
接下来,进行尺度缩放,然后进行softmax归一化。具体来说,就是将点乘积的结果除以一个常数,这个值一般是采用上文提到的矩阵的第一个维度的开方,这里我们除以8,即64的开方8,当然也可以选择其他的值。然后把得到的结果做一个softmax的计算。得到的结果即是每个词对于当前位置的词的相关性大小。当然,当前单词与其自身的Self-Attention Score一般最大,即当前位置的词相关性很大,其他单词根据与当前单词==相关性(重要程度)==有对应的Self-Attention Score。
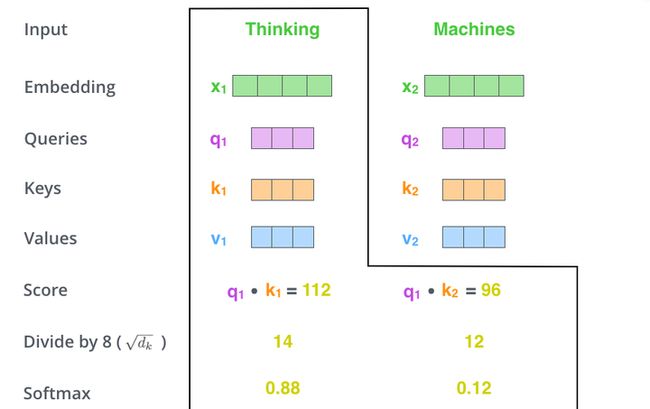
Step 4——
下一步,就是把Value向量和softmax得到的值进行相乘,并相加,得到的结果即是self-attetion在当前节点的值,该值所表达的就是每个单词在这个句子当中的意思。
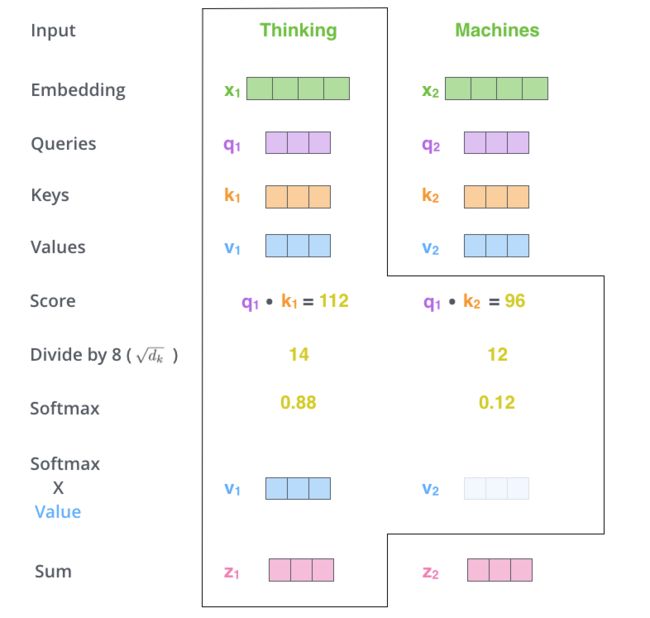
4.3 QKV矩阵的概念
如果将输入的所有向量合并为矩阵形式,则所有QKV向量可以合并为QKV矩阵形式表示:
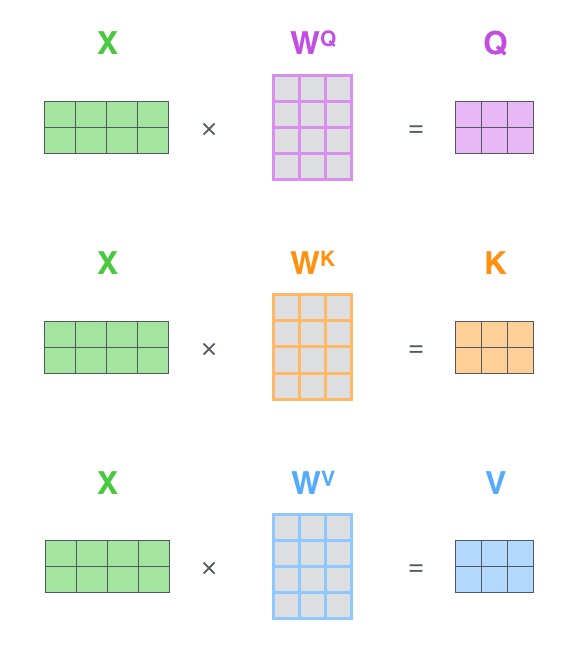
其中, W Q , W K , W V W^{Q},W^{K},W^{V} WQ,WK,WV 是模型训练过程学习到的合适的参数,其初始值通过随机初始化。
在实际的应用场景,为了提高计算速度,我们采用的是矩阵的方式,直接计算出Query, Key, Value的矩阵,然后把embedding的值与三个矩阵直接相乘,把得到的新矩阵 Q 与 K 相乘,除以一个常数,做softmax操作,最后乘上 V 矩阵。则Self-Attention计算过程可以简化为:

上式是Self-Attention的公式,Q和K的点乘表示Q和K矩阵之间的相似程度,但是这个相似度不是归一化的,所以需要一个softmax将Q和K的结果进行归一化,那么softmax后的结果就是一个所有数值为0-1的mask矩阵(可以理解为Attention Score矩阵),而V矩阵表示输入线性变化后的特征,那么将mask矩阵乘上V矩阵就能得到加权后的特征。总结一下,Q和K矩阵的引入是为了得到一个所有数值为0-1的mask矩阵,V矩阵的引入是为了保留输入的特征(原始特征)。通过 query 和 key 的相似性程度来确定 value 的权重分布的方法,被称为 scaled dot-product attention。
QKV来自于同一个句子表征,Q是目标词矩阵,K是关键词矩阵,V是原始特征,通过三步计算:
- Q和K进行点积计算,得到相似度矩阵;
- softmax归一化相似度矩阵,得到相似度权重;
- 将相似度权重和V矩阵加权求和,得到强化表征Z。
4.4 总结
那么重点来了,第一个问题:Self-Attention 结构的最初输入 Q(查询), K(键值), V(值) 这三个矩阵怎么理解呢?其代表什么,通过什么计算而来?
在 Self-Attention 中,Q、K、V 是在同一个输入序列(比如序列中的一个单词)上计算得到的三个向量。具体来说,我们可以通过对原始输入词的 embedding 进行线性变换(比如使用一个全连接层),来得到 Q、K、V。
第二个问题:Self-Attention 结构怎么理解,Q、K、V的作用是什么?这三个矩阵又怎么计算得到最后的输出?
在计算 Self-Attention 时,Q、K、V 被用来计算注意力分数,即用于表示当前位置和其他位置之间的关系。注意力分数可以通过 Q 和 K 的点积来计算,然后将分数除以 8,再经过一个 softmax 归一化处理,得到每个位置的权重。然后用这些权重来加权计算 V 的加权和,即得到当前位置的输出。
4.5 Self-Attention的缺陷
在Self-Attention模型中,输入是一整排tokens,对于人类来说,我们很容易知道tokens的位置信息,比如:
- 绝对位置信息。a1是第一个token,a2是第二个token…
- 相对位置信息。a2在a1的后面一位,a4在a2的后面两位…
- 不同位置间的距离。a1和a3相差两个位置,a1和a4相差三个位置…
这些对于Self-Attention来说,是无法分辨的信息,因为Self-Attention的运算是无向的。
5. Multihead Attention
5.0 Multihead Attention基础单元
Multi-Head Attention (MHA) 是基于 Self-Attention (SA) 的一种变体。MHA 在 SA 的基础上引入了“多头”机制,将输入拆分为多个子空间,每个子空间分别执行 SA,最后将多个子空间的输出拼接在一起并进行线性变换,从而得到最终的输出。Multi-Head Attention 机制对自注意力机制进行拓展,允许模型联合学习序列的不同表示子空间。
对于 MHA,之所以需要对 Q、K、V 进行多头(head)划分,其目的是为了增强模型对不同信息的关注。具体来说,多组 Q、K、V 分别计算 Self-Attention,每个头自然就会有独立的 Q、K、V 参数,从而让模型同时关注多个不同的信息,这有些类似 CNN 架构模型的多通道机制。通俗理解,“多头注意力"就是进行多次自注意力计算,每次计算一个序列的自注意力被称为一个"头”,每个"头"可能对应着不同的问题,例如第一个"头"可能关注"发生了什么",第二个"头"可能关注"何时发生",第三个"头"可能关注"与谁有关"等等。下图是论文中 Multi-Head Attention 的结构图。
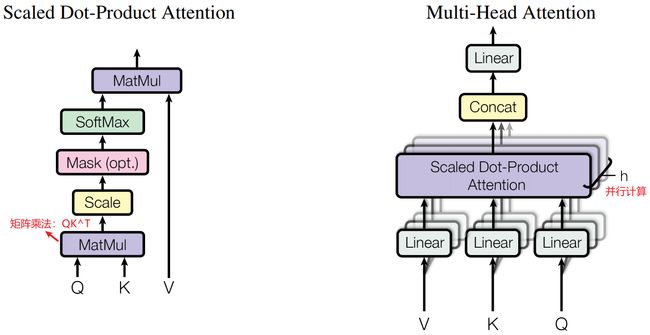
从图中可以看出, MHA 结构的计算过程可总结为下述步骤:
- 将输入 Q、K、V 张量进行线性变换(Linear 层),输出张量尺寸为
[batch_size, seq_len, d_model]; - 将前面步骤输出的张量,按照头的数量(n_head)拆分为 n_head 子张量,其尺寸为
[batch_size, n_head, seq_len, d_model//n_head]; - 每个子张量并行计算注意力分数,即执行
dot-product attention层,输出张量尺寸为[batch_size, n_head, seq_len, d_model//n_head]; - 将这些子张量进行拼接
concat,并经过线性变换得到最终的输出张量,尺寸为[batch_size, seq_len, d_model]。
总结:因为 GPU 的并行计算特性,步骤2中的张量拆分和步骤4中的张量拼接,其实都是通过 review 算子来实现的。同时,也能发现SA 和 MHA 模块的输入输出矩阵维度都是一样的。
5.1 多头注意力的计算过程
多头注意力将输入序列重复进行自注意力计算n次,每次使用不同的权重矩阵,得到n个注意力向量序列。然后将这n个序列拼接并线性转换,得到最终的序列表示,即:
M u l t i H e a d ( Q , K , V ) = c o n c a t ( h e a d 1 , . . . , h e a d n ) W o w h e r e h e a d i = A t t e n t i o n ( W i Q Q , W i K K , W i V V ) MultiHead(Q,K,V)=concat(head_1,...,head_n)W_o \\ where\:head_i=Attention(W_i^QQ,W_i^KK,W_i^VV) MultiHead(Q,K,V)=concat(head1,...,headn)Wowhereheadi=Attention(WiQQ,WiKK,WiVV)
一般用 d_model 表示输入嵌入向量的维度, n_head 表示分割成多少个头,因此,d_model//n_head 自然表示每个头的输入和输出维度。在论文中。 d_model = 512,n_head = 8,d_model//n_head = 64。值得注意的是,由于每个头的维数减少,总计算成本与具有全维的单头注意力是相似的。
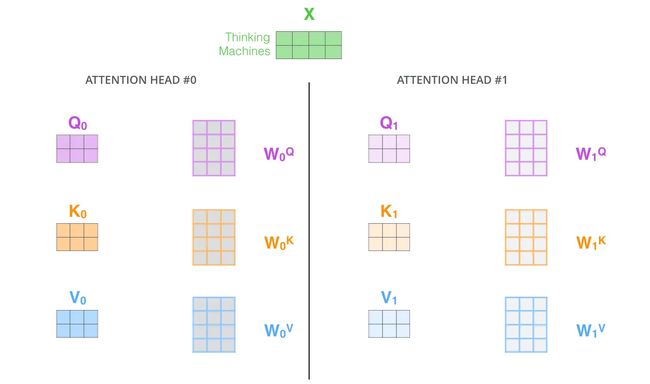

多头注意力的计算过程与自注意力基本一致,但是使用了不同的权重矩阵,并且将所有的注意力向量(一般情况下是8个)进行拼接,再乘以一个权重矩阵,最后得到的结果就是多头注意力的输出。在实际计算中,由于不同"头"的计算互不影响,可以同时计算所有的"头",即并行计算,以提高计算效率。
总的来说,多头注意力机制可以为每个单词学习到更丰富、更好的表示,每个"头"都能从不同的角度去理解序列中的每个单词。
5.2 encoder&decoder
Multihead Attention单元中的encoder,就是叠加多个Multihead Attention基本单元。其中K,Q,V均来自前一层encoder的输出,即encoder的每个位置都可以注意到之前一层encoder的所有位置。
对于decoder来说,有两个与encoder不同的地方。一个是第一级的Masked Multihead,另一个是第二级的Multi-Head Attention不仅接收来自前一级的输出,还要接收encoder的输出。

第一级decoder的key,query,value均来自前一层decoder的输出,但加入了Mask操作,即我们只能attend到前面已经翻译过的输出的词语,因为当前的翻译过程并不知道下一个输出词语,这是之后才会推测到的。
第二级decoder也被称作encoder-decoder attention layer,即它的Q来自于之前一级的decoder层的输出,但其key和value来自于encoder的输出,这使得decoder的每一个位置都可以attend到输入序列的每一个位置。
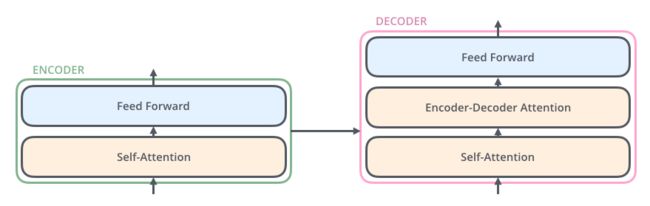
总结一下,key和value的来源总是相同的,q在encoder以及第一级decoder中与key,value来源相同,在encoder-decoder attention layer中与key,value来源不同。
6. Attention与Self-Attention对比
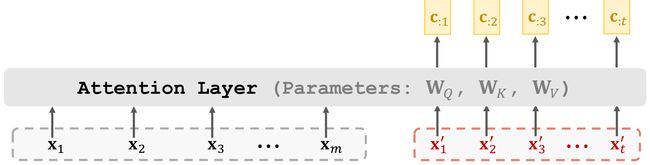
6.1 Attention layer
- Attention layer: C = A t t n ( X , X ′ ) \mathrm{C}=\mathrm{Attn}(\mathbf{X},\mathbf{X}^{\prime}) C=Attn(X,X′).
- Query: q : j = W Q x j ′ \mathbf{q}_{:j}=\mathbf{W}_Q\mathbf{x}_j^{\prime} q:j=WQxj′.
- Key: k : i = W K x i \mathbf{k}_{:i}=\mathbf{W}_K\mathbf{x}_i k:i=WKxi.
- Value: v : i = W V x i \mathbf{v}_{:i}=\mathbf{W}_V\mathbf{x}_i v:i=WVxi.
- Output: c ; j = V ⋅ S o f t m a x ( K T q : j ) \mathrm{c}_{;j}=\mathrm{V}\cdot\mathrm{Softmax}(\mathbb{K}^T\mathbf{q}_{:j}) c;j=V⋅Softmax(KTq:j).
6.2 Self-Attention Layer
- Attention layer: C = A t t n ( X , X ′ ) \mathcal{C}=\mathrm{Attn}(\mathbf{X},\mathbf{X}^{\prime}) C=Attn(X,X′).
- Self-Attention layer: C = Attn ( X , X ) C=\operatorname{Attn}(\mathbf{X},\mathbf{X}) C=Attn(X,X).

7. Self-Attention代码实现
这里仅分析核心代码,详细代码请查阅:tensor2tensor/layers/common_attention.py
multihead_attention()
def multihead_attention(query_antecedent,
memory_antecedent,
...):
"""Multihead scaled-dot-product attention with input/output transformations.
Args:
query_antecedent: a Tensor with shape [batch, length_q, channels]
memory_antecedent: a Tensor with shape [batch, length_m, channels] or None
...
Returns:
The result of the attention transformation. The output shape is
[batch_size, length_q, hidden_dim]
"""
#计算q, k, v矩阵
q, k, v = compute_qkv(query_antecedent, memory_antecedent, ...)
#计算dot_product的attention
x = dot_product_attention(q, k, v, ...)
x = common_layers.dense(x, ...)
return x
compute_qkv()
def compute_qkv(query_antecedent,
memory_antecedent,
...):
"""Computes query, key and value.
Args:
query_antecedent: a Tensor with shape [batch, length_q, channels]
memory_antecedent: a Tensor with shape [batch, length_m, channels]
...
Returns:
q, k, v : [batch, length, depth] tensors
"""
# 注意这里如果memory_antecedent是None,它就会设置成和query_antecedent一样,encoder的
# self-attention调用时memory_antecedent 传进去的就是None。
if memory_antecedent is None:
memory_antecedent = query_antecedent
q = compute_attention_component(
query_antecedent,
...)
# 注意这里k,v均来自于memory_antecedent。
k = compute_attention_component(
memory_antecedent,
...)
v = compute_attention_component(
memory_antecedent,
...)
return q, k, v
def compute_attention_component(antecedent,
...):
"""Computes attention compoenent (query, key or value).
Args:
antecedent: a Tensor with shape [batch, length, channels]
name: a string specifying scope name.
...
Returns:
c : [batch, length, depth] tensor
"""
return common_layers.dense(antecedent, ...)
dot_product_attention()
def dot_product_attention(q,
k,
v,
...):
"""Dot-product attention.
Args:
q: Tensor with shape [..., length_q, depth_k].
k: Tensor with shape [..., length_kv, depth_k]. Leading dimensions must
match with q.
v: Tensor with shape [..., length_kv, depth_v] Leading dimensions must
match with q.
Returns:
Tensor with shape [..., length_q, depth_v].
"""
# 计算Q, K的矩阵乘积。
logits = tf.matmul(q, k, transpose_b=True)
# 利用softmax将结果归一化。
weights = tf.nn.softmax(logits, name="attention_weights")
# 与V相乘得到加权表示。
return tf.matmul(weights, v)
transformer_encoder()
def transformer_encoder(encoder_input,
hparams,
...):
"""A stack of transformer layers.
Args:
encoder_input: a Tensor
hparams: hyperparameters for model
...
Returns:
y: a Tensors
"""
x = encoder_input
with tf.variable_scope(name):
for layer in range(hparams.num_encoder_layers or hparams.num_hidden_layers):
with tf.variable_scope("layer_%d" % layer):
with tf.variable_scope("self_attention"):
# layer_preprocess及layer_postprocess包含了一些layer normalization
# 及residual connection, dropout等操作。
y = common_attention.multihead_attention(
common_layers.layer_preprocess(x, hparams),
#这里注意encoder memory_antecedent设置为None
None,
...)
x = common_layers.layer_postprocess(x, y, hparams)
with tf.variable_scope("ffn"):
# 前馈神经网络部分。
y = transformer_ffn_layer(
common_layers.layer_preprocess(x, hparams),
hparams,
...)
x = common_layers.layer_postprocess(x, y, hparams)
return common_layers.layer_preprocess(x, hparams)
transformer_decoder()
def transformer_decoder(decoder_input,
encoder_output,
hparams,
...):
"""A stack of transformer layers.
Args:
decoder_input: a Tensor
encoder_output: a Tensor
hparams: hyperparameters for model
...
Returns:
y: a Tensors
"""
x = decoder_input
with tf.variable_scope(name):
for layer in range(hparams.num_decoder_layers or hparams.num_hidden_layers):
layer_name = "layer_%d" % layer
with tf.variable_scope(layer_name):
with tf.variable_scope("self_attention"):
# decoder一级memory_antecedent设置为None
y = common_attention.multihead_attention(
common_layers.layer_preprocess(x, hparams),
None,
...)
x = common_layers.layer_postprocess(x, y, hparams)
if encoder_output is not None:
with tf.variable_scope("encdec_attention"):
# decoder二级memory_antecedent设置为encoder_output
y = common_attention.multihead_attention(
common_layers.layer_preprocess(x, hparams),
encoder_output,
...)
x = common_layers.layer_postprocess(x, y, hparams)
with tf.variable_scope("ffn"):
y = transformer_ffn_layer(
common_layers.layer_preprocess(x, hparams),
hparams,
...)
x = common_layers.layer_postprocess(x, y, hparams)
return common_layers.layer_preprocess(x, hparams)