【Python人工智能】Python全栈体系（二十一）

人工智能

第十二章 聚类模型

一、聚类问题概述

聚类（cluster）与分类（class）问题不同，聚类是属于无监督学习模型，而分类属于有监督学习。聚类使用一些算法把样本分为N个群落，群落内部相似度较高，群落之间相似度较低。在机器学习中，通常采用“距离”来度量样本间的相似度，距离越小，相似度越高；距离越大，相似度越低.

1. 相似度度量方式

① 欧氏距离

相似度使用欧氏距离来进行度量. 坐标轴上两点$x_1,x_2$之间的欧式距离可以表示为：
$$|x_1-x_2|=\sqrt{(x_1-x_2{)}^2}$$
平面坐标中两点$(x_1,y_1),(x_2,y_2)$欧式距离可表示为：
$$|(x_1,y_1)-(x_2,y_2)|=\sqrt{(x_1-x_2{)}^2+(y_1-y_2{)}^2}$$
三维坐标系中$(x_1,y_1,z_1),(x_2,y_2,z_2)$欧式距离可表示为：
$$|(x_1,y_1,z_1),(x_2,y_2,z_2)|=\sqrt{(x_1-x_2{)}^2+(y_1-y_2{)}^2+(z_1-z_2{)}^2}$$
以此类推，可以推广到N维空间.
$$|(x_1,y_1,z_1...,n_1),(x_2,y_2,z_2,...n_2)|=\sqrt{(x_1-x_2{)}^2+(y_1-y_2{)}^2+(z_1-z_2{)}^2+...(n_1-n_2{)}^2}$$

② 曼哈顿距离

二维平面两点$a(x_1,y_1)$与$b(x_2,y_2)$两点间的曼哈顿距离为：
$$d(a,b)=|x_1-x_2|+|y_1-y_2|$$
推广到N维空间，$x(x_1,x_2,...,x_n)$与$y(y_1,y_2,...,y_n)$之间的曼哈顿距离为：
$$d(x,y)=|x_1-y_1|+|x_2-y_2|+...+|x_n-y_n|=\sum _{i=1}^n|x_i-y_i|$$

在上图中，绿色线条表示的为欧式距离，红色线条表示的为曼哈顿距离，黄色线条和蓝色线条表示的为曼哈顿距离的等价长度。

③ 闵可夫斯基距离

闵可夫斯基距离（Minkowski distance）又称闵氏距离，其定义为：
$$D(x,y)=(\sum _{i=1}^n|x_i-y_i{|}^p{)}^{\frac{1}{p}}$$

• 当$p=1$时，即为曼哈顿距离

• 当$p=2$时，即为欧式距离

• 当$p\to \infty$时，即为切比雪夫距离

可见，曼哈顿距离、欧氏距离、切比雪夫距离都是闵可夫斯基的特殊形式.

④ 距离的性质

如果$dist(x,y)$度量标准为一个距离，它应该满足以下几个条件：

• 非负性：距离一般不能为负，即 $dist(x,y)>=0$
• 同一性：$dist(x_i,y_i)=0$，当且仅当$x_i=y_i$
• 对称性：$dist(x_i,y_i)=dist(y_i,x_i)$
• 直递性：$dist(x_i,x_j)<=dist(x_i,x_k)+dist(x_k,x_j)$

2. 聚类算法的划分

① 原型聚类

原型聚类也称“基于原型的聚类”（prototype-based clustering），此类算法假设聚类结构能通过一组原型刻画，在现实聚类任务中极为常用. 通常情况下，算法先对原型进行初始化，然后对原型进行迭代更新求解. 采用不同的原型表示、不同的求解方式，将产生不同的算法. 最著名的原型聚类算法有K-Means.

② 密度聚类

密度聚类也称“基于密度的聚类”（density-based clustering），此类算法假定聚类结构能通过样本分布的紧密程度确定. 通常情况下，密度聚类算法从样本密度的角度来考察样本之间的可连接性，并基于可连接样本不断扩展聚类簇以获得最终的聚类结果. 著名的密度聚类算法有DBSCAN.

③ 层次聚类

层次聚类（hierarchical clustering）试图在不同层次对数据集进行划分，从而形成树形的聚类结构. 数据集的划分可以采用“自底向上”或“自顶向下”的策略. 常用的层次聚类有凝聚层次算法等.

二、常用聚类算法

1. K均值聚类

① 定义

K均值聚类（k-means clustering）算法是一种常用的、基于原型的聚类算法，简单、直观、高效。其步骤为：

第一步：根据事先已知的聚类数，随机选择若干样本作为聚类中心，计算每个样本与每个聚类中心的欧式距离，离哪个聚类中心近，就算哪个聚类中心的聚类，完成一次聚类划分.

第二步：计算每个聚类的几何中心，如果几何中心与聚类中心不重合，再以几何中心作为新的聚类中心，重新划分聚类. 重复以上过程，直到某一次聚类划分后，所得到的各个几何中心与其所依据的聚类中心重合或足够接近为止. 聚类过程如下图所示：

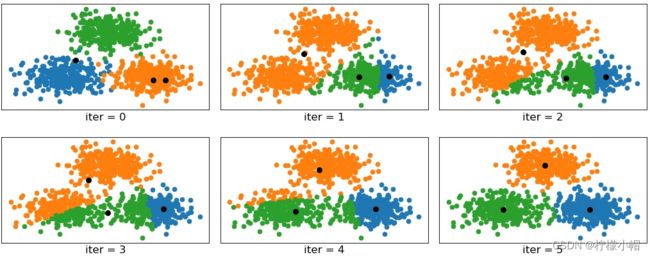
注意事项：

（1）聚类数（K）必须事先已知，来自业务逻辑的需求或性能指标.

（2）最终的聚类结果会因初始中心的选择不同而异，初始中心尽量选择离中心最远的样本.

② 算法特点

• 聚类数（K）必须事先已知，借助某些评估指标（轮廓系数），优选最好的聚类数。

• 聚类中心的初始选择会影响到最终聚类划分的结果。初始中心尽量选择距离较远的样本。

③ 实现

• sklearn 提供了 k-means 聚类模型相关API：

import sklearn.cluster as sc
# n_clusters : 聚类数
model = sc.KMeans(n_clusters=4)
# 不断调整聚类中心，知道最终聚类中心稳定则聚类完成
model.fit(x)
# 获取训练结果的聚类中心
labels = model.labels_
centers = model.cluster_centers_
pred_y = model.predict(x)

import numpy as np
import pandas as pd
import sklearn.cluster as sc

# 加载数据
data = pd.read_csv('multiple3.txt', header=None)
data.plot.scatter(x=0, y=1, s=50)

model = sc.KMeans(n_clusters=4)
model.fit(data)
labels = model.labels_
ax = data.plot.scatter(x=0, y=1, c=labels, cmap='brg', s=50)
# 获取四个聚类中心
centers = model.cluster_centers_
centers = pd.DataFrame(centers)
centers.plot.scatter(x=0, y=1, c='red', marker='+', s=300, ax=ax)

④ 特点及使用

• 优点

（1）原理简单，实现方便，收敛速度快；

（2）聚类效果较优，模型的可解释性较强；

• 缺点

（1）需要事先知道聚类数量；

（2）聚类初始中心的选择对聚类结果有影响；

（3）采用的是迭代的方法，只能得到局部最优解；

（4）对于噪音和异常点比较敏感.

• 什么时候选择k-means

（1）事先知道聚类数量

（2）数据分布有明显的中心

2. 轮廓系数

• 轮廓系数是用于评估聚类效果的指标。好的聚类具备内密外疏的特点，同一个聚类内部的样本要足够密集，不同聚类之间样本要足够疏远。
• 轮廓系数计算规则：针对样本空间中的一个特定样本，计算它与所在聚类其它样本的平均距离a，以及该样本与距离最近的另一个聚类中所有样本的平均距离b，该样本的轮廓系数为(b-a)/max(a,b) ，将整个样本空间中所有样本的轮廓系数取算数平均值，作为聚类划分的性能指标s。
• 轮廓系数的区间为：[-1, 1]。-1代表分类效果差，1代表分类效果好。0代表聚类重叠，没有很好的划分聚类。
• 轮廓系数实现
  • sklearn 提供了轮廓系数相关API：

import sklearn.metrics as sm
# v: 平均轮廓系数
# metric: 距离算法：使用欧几里得距离（euclidean）
v = sm.silhouette_score(输入集, 输出集, sample_size=样本数, metric=距离算法)

import sklearn.metrics as sm
model = sc.KMeans(n_clusters=4)
model.fit(data)
labels = model.labels_

# 计算轮廓系数
s = sm.silhouette_score(data, labels, sample_size=len(data), metric='euclidean')
print(s) # 0.5773232071896658

3. 噪声密度

① 定义

噪声密度（Density-Based Spatial Clustering of Applications with Noise， 简写DBSCAN）随机选择一个样本做圆心，以事先给定的半径做圆，凡被该圆圈中的样本都被划为与圆心样本同处一个聚类，再以这些被圈中的样本做圆心，以事先给定的半径继续做圆，不断加入新的样本，扩大聚类的规模，知道再无新的样本加入为止，即完成一个聚类的划分. 以同样的方法，在其余样本中继续划分新的聚类，直到样本空间被耗尽为止，即完成整个聚类划分过程. 示意图如下：

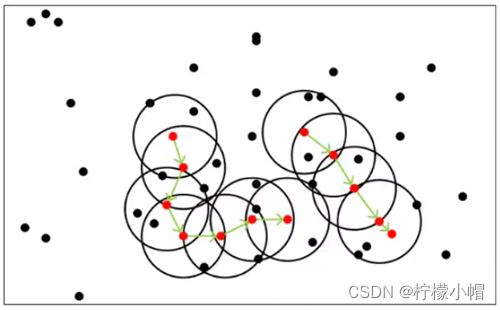
DBSCAN算法中，样本点被分为三类：

• 边界点（Border point）：可以划分到某个聚类，但无法发展出新的样本；

• 噪声点（Noise）：无法划分到某个聚类中的点；

• 核心点（Core point）：除了孤立样本和外周样本以外的样本都是核心点；
  
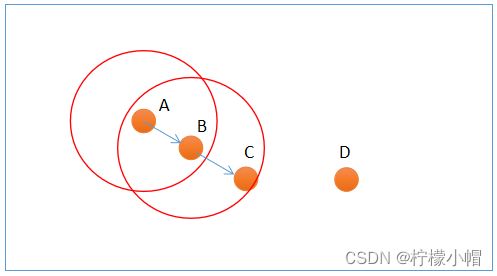
  上图中，A和B为核心点，C为边界点，D为噪声点. 此外，DBSCAN还有两个重要参数：

• 邻域半径：设置邻域半径大小；

• 最少样本数目：邻域内最小样本数量，某个样本邻域内的样本超过该数，才认为是核心点.

② 算法特点

• 事先给定的半径会影响最后的聚类效果，可以借助轮廓系数选择较优的方案。
• 根据聚类的形成过程，把样本细分为以下三类：
  • 外周样本：被其它样本聚集到某个聚类中，但无法再引入新样本的样本。
  • 孤立样本：聚类中的样本数低于所设定的下限，则不称其为聚类，反之称其为孤立样本。
  • 核心样本：除了外周样本和孤立样本以外的样本。

③ 算法实现

• sklearn 提供了 DBSCAN 算法的实现如下：

# DBSCAN 聚类器
# eps: 半径
# min_samples: 聚类样本数的下限，若低于该数值，则称为孤立样本
model = sc.DBSCAN(eps=epsilon, min_sample=5)
model.fit(x)
model.core_sample_indices_

④ 特点及使用

• 算法优点

（1）不用人为提前确定聚类类别数K；
（2）聚类速度快；
（3）能够有效处理噪声点（因为异常点不会被包含于任意一个簇，则认为是噪声）；
（4）能够应对任意形状的空间聚类.

• 算法缺点

（1）当数据量过大时，要求较大的内存支持I/O消耗很大；
（2）当空间聚类的密度不均匀、聚类间距差别很大时、聚类效果有偏差；
（3）邻域半径和最少样本数量两个参数对聚类结果影响较大.

• 何时选择噪声密度

（1）数据稠密、没有明显中心；

（2）噪声数据较多；

（3）未知聚簇的数量.

import numpy as np
import pandas as pd
import sklearn.cluster as sc

# 加载数据
data = pd.read_csv('multiple3.txt', header=None)
data.plot.scatter(x=0, y=1, s=50)

# DBSCAN 算法实现聚类
# 创建DBSCAN模型并训练模型
params = np.arange(0.5, 1.0, 0.1)
models, scores, epss = [], [], []
for param in params:
    model = sc.DBSCAN(eps=param, min_samples=5)
    model.fit(data)
    labels = model.labels_
    # labels # -1很多，所以有很多孤立样本，半径太小
    score = sm.silhouette_score(data, labels, sample_size=len(data), metric='euclidean')
    models.append(model)
    scores.append(score)
    epss.append(param)

    
best_ind = np.argmax(scores)
best_model = models[best_ind]
best_score = scores[best_ind]
best_eps = epss[best_ind]
best_model, best_score, best_eps
"""
(DBSCAN(eps=0.7999999999999999), 0.41779833446624154, 0.7999999999999999)
"""

# 利用最优模型绘图
labels = best_model.labels_
data.plot.scatter(x=0, y=1, s=50, c=labels, cmap='brg')