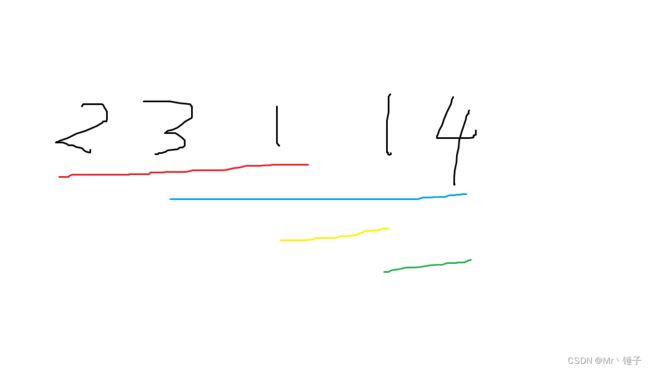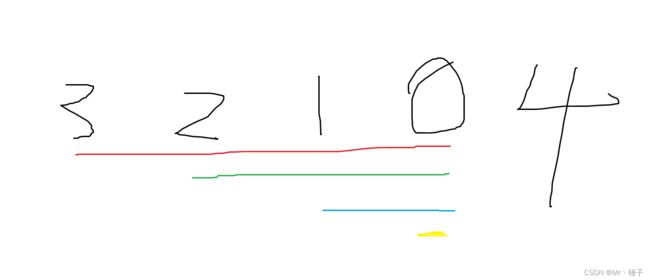实验三--贪心算法的设计与分析

某不知名学校算法课第三次实验报告

题目来自力扣 这次实验是贪心算法

贪心的思维很跳跃，每道题也没有固定的模板的思考方向

跳跃游戏

题目描述：

给定一个非负整数数组，你最初位于数组的第一个位置。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个位置。

示例 1:

输入: [2,3,1,1,4]

输出: true

解释: 我们可以先跳 1 步，从位置 0 到达 位置 1, 然后再从位置 1 跳 3 步到达最后一个位置。

示例 2:

输入: [3,2,1,0,4]

输出: false

解释: 无论怎样，你总会到达索引为 3 的位置。但该位置的最大跳跃长度是 0 ， 所以你永远不可能到达最后一个位置。

我们把数组中的每个元素看作是最大覆盖范围，当覆盖范围到达终点时，即满足题目条件

以样例1为例 初始指向2 覆盖范围为231，更新至3 覆盖范围3114 到达终点 符合题意

以样例2为例 初始指向3 覆盖范围3210 指向2 覆盖范围210 指向1 覆盖范围10 指向0 覆盖范围0

可以看到 我们没有办法覆盖到终点4 所以不符合题意

代码加注释如下：

class Solution {
public:
    bool canJump(vector& nums) {
        int cover = 0;
        for(int i = 0; i <= cover; i ++ )
        {
            //不断更新自己的覆盖范围
            cover = max(cover, nums[i] + i);
            //如果覆盖范围能到达终点
            if(cover >= nums.size() - 1) return true;
        }
        return false;
    }
};

很短，但是很需要思维，这就是贪心 也是传说中的局部最优解到全局最优解

分割平衡字符串

题目描述：

在一个「平衡字符串」中，'L' 和 'R' 字符的数量是相同的。

给出一个平衡字符串 s，请你将它分割成尽可能多的平衡字符串。

返回可以通过分割得到的平衡字符串的最大数量。

示例 1：

输入：s = "RLRRLLRLRL"

输出：4

解释：s 可以分割为 "RL", "RRLL", "RL", "RL", 每个子字符串中都包含相同数量的 'L' 和 'R'。

示例 2：

输入：s = "RLLLLRRRLR"

输出：3

解释：s 可以分割为 "RL", "LLLRRR", "LR", 每个子字符串中都包含相同数量的 'L' 和 'R'。

示例 3：

输入：s = "LLLLRRRR"

这道题可以暴力 数据不大 但是感觉这种查询匹配问题 用哈希表的方式解决是通常的选择

计数L 发现R计数相等时 就是一对平衡字串 思路很简单

代码如下：

class Solution {
public:
    int balancedStringSplit(string s) {
      int cnt = 0; //记录L R的数量关系
      int res = 0;
      for(char c : s) // 遍历
      {
        if( c == 'L' ) cnt ++ ;
        else cnt --;
        if( cnt == 0 ) res ++ ;
      }
      return res;
    }
};

用户分组

题目描述：

有 n 位用户参加活动，他们的 ID 从 0 到 n - 1，每位用户都 恰好 属于某一用户组。给你一个长度为 n 的数组 groupSizes，其中包含每位用户所处的用户组的大小，请你返回用户分组情况（存在的用户组以及每个组中用户的 ID）。

你可以任何顺序返回解决方案，ID 的顺序也不受限制。此外，题目给出的数据保证至少存在一种解决方案。

示例 1：

输入：groupSizes = [3,3,3,3,3,1,3]

输出：[[5],[0,1,2],[3,4,6]]

解释：

其他可能的解决方案有 [[2,1,6],[5],[0,4,3]] 和 [[5],[0,6,2],[4,3,1]]。

示例 2：

输入：groupSizes = [2,1,3,3,3,2]

输出：[[1],[0,5],[2,3,4]]

 提示：

groupSizes.length == n

1 <= n <= 500

1 <= groupSizes[i] <= n

从题目中，我们知道要填入的数据是0 ~n-1的连续整数，也正好对应了数组的下标

然后给的函数要返回双层vector，也就是说我们得要一个单层vector填入

跟上一题差不多，也是用一个类似哈希表的写法，进行查询和匹配的问题

代码＋注释如下：

class Solution {
public:
    vector> groupThePeople(vector& groupSizes) {
        vector> res; 
        //二维vector只能用一级vector去push——back
        unordered_map>M; //哈希表
        int cnt = 0; // 记录数组下标 正好是0~n-1号数字
        
        for(auto x : groupSizes) //强化for循环
        {
            M[x].push_back(cnt);
            //该组存满了
            if(M[x].size() >= x) 
            {
                //存入答案
                res.push_back(M[x]);
                //同时清空
                M[x].clear();
            }
            cnt ++;
        }
        
        return res;
    }
};

非递增顺序的最小子序列

题目描述：

给你一个数组 nums，请你从中抽取一个子序列，满足该子序列的元素之和 严格 大于未包含在该子序列中的各元素之和。

如果存在多个解决方案，只需返回 长度最小 的子序列。如果仍然有多个解决方案，则返回 元素之和最大 的子序列。

与子数组不同的地方在于，「数组的子序列」不强调元素在原数组中的连续性，也就是说，它可以通过从数组中分离一些（也可能不分离）元素得到。

注意，题目数据保证满足所有约束条件的解决方案是 唯一 的。同时，返回的答案应当按 非递增顺序 排列。

示例 1：

输入：nums = [4,3,10,9,8]

输出：[10,9]

解释：子序列 [10,9] 和 [10,8] 是最小的、满足元素之和大于其他各元素之和的子序列。但是 [10,9] 的元素之和最大。 

示例 2：

输入：nums = [4,4,7,6,7]

输出：[7,7,6]

解释：子序列 [7,7] 的和为 14 ，不严格大于剩下的其他元素之和（14 = 4 + 4 + 6）。因此，[7,6,7] 是满足题意的最小子序列。注意，元素按非递增顺序返回。

简单贪心题，我们先进行一遍排序，从最大的数字开始选，选到答案集合中的数的和大于剩下的数的和即可

代码＋注释如下：

class Solution {
public:
    vector minSubsequence(vector& nums) {
        vector res; // 存答案 返回值是vector
        sort(nums.begin(),nums.end()); // 排序
        int sum = 0, cur = 0, idx = nums.size() - 1;
        for(int i : nums) sum += i;
        while(cur <= sum) //答案序列和小于剩余序列和
        {
            sum -= nums[idx];
            cur += nums[idx];
            res.push_back(nums[idx--]); // 加入答案序列 顺便往前选择

        }
        return res;
    }
};