深度学习笔记之优化算法(二)随机梯度下降

引言

本节将介绍随机梯度下降$\text{(Stochastic Gradient Descent,SGD)}$

回顾：梯度下降法

从最速下降法的角度观察，下降方向${\mathcal{P}}_k$的判定逻辑是：满足目标函数$f(x_{k+1})=f(x_k+{\alpha }_k\cdot {\mathcal{P}}_k)$的一阶泰勒展开式与$f(x_k)$之间存在严格的单调性；
其中$\mathcal{O}(\Vert {\alpha }_k{\mathcal{P}}_k\Vert )$表示关于${\alpha }_k{\mathcal{P}}_k$的高阶无穷小;
$$\begin{array}{rl}f(x_{k+1})-f(x_k)& ={\alpha }_k\cdot ({\mathcal{P}}_k{)}^T\nabla f(x_k)+\mathcal{O}(\Vert {\alpha }_k{\mathcal{P}}_k\Vert )\\ & \approx {\alpha }_k\cdot ({\mathcal{P}}_k{)}^T\nabla f(x_k)<0\\ & \Rightarrow ({\mathcal{P}}_k{)}^T\nabla f(x_k)<0\end{array}$$
对上式进行展开，如果使用欧式范数对${\mathcal{P}}_k$的大小进行描述，即：
$$({\mathcal{P}}_k{)}^T\nabla f(x_k)=\Vert {\mathcal{P}}_k{\Vert }_2\cdot \Vert \nabla f(x_k){\Vert }_2\cdot \cos \theta$$
关于更新方向${\mathcal{P}}_k$，我们更关注它的方向朝向，而不是它的大小。因而对更新方向${\mathcal{P}}_k$的大小进行约束。例如：$\Vert {\mathcal{P}}_k\Vert \le 1$。由于$\nabla f(x_k)$是大小恒正的已知项，因而真正影响$({\mathcal{P}}_k{)}^T\nabla f(x_k)$结果的只有梯度向量$\nabla f(x_k)$与更新方向${\mathcal{P}}_k$之间的夹角$\theta$。

由于$\cos \theta \in [-1,1]$，因而当$\begin{array}{r}\theta =\frac{\pi }{2}\end{array}$时，即更新方向与梯度方向相反时，$\cos \theta =-1$，$({\mathcal{P}}_k{)}^T\nabla f(x_k)$达到最小：
$${\mathcal{P}}_k=-\nabla f(x_k)$$
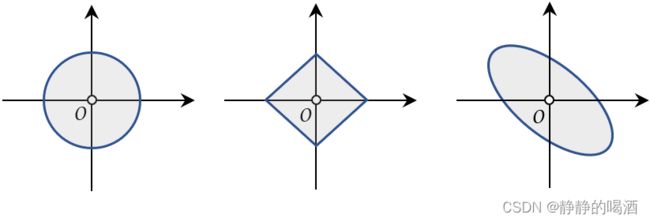
此时的最速下降法就是梯度下降法。但如果对${\mathcal{P}}_k$的约束方式不是欧式范数，如：${\mathcal{L}}_1$范数或者矩阵$2$-范数，它们在范数范围内，不同方向的最大值可能不相等。见下图：

• 其中最左侧的是欧式范数$\Vert \mathcal{P}{\Vert }_2\le ϵ$,可以看出，特征空间原点到范数边界的距离均相等，这使得上式唯一的可变信息取决于$\theta$的取值；
• 中间与右侧分别是${\mathcal{L}}_1$范数$\Vert \mathcal{P}{\Vert }_1\le ϵ$与矩阵$2$-范数$\Vert \mathcal{A}{\Vert }_2\le ϵ$,可以看出：由于特征空间原点到范数边界之间的距离可能不相等，这使得上式的可变信息取决于$\theta$、范数长度的共同作用,最终可能导致:某方向即便不是负梯度方向，但它有可能使$({\mathcal{P}}_k{)}^T\nabla f(x_k)$达到最小。
  

梯度下降法在机器学习中的问题

在本节中，这里暂时模糊掉最速下降法与梯度下降法之间的区别。在无约束优化问题——最速下降法以及梯度下降法在强凸函数的收敛性分析中介绍过，如：

• 梯度下降法收敛速度慢，即便目标函数是强凸函数最快也仅能达到线性收敛；
• $\text{Hessian Matrix}\Rightarrow {\nabla }^{2}f(\cdot )$以及条件数$(\text{Condition Number})$对收敛速度的影响。当条件数越大时，收敛速度随之减缓，极限时可退化至次线性收敛；
• 关于收敛方向：可能出现$\text{ZigZag}$现象。底层原因在于：每次迭代过程，负梯度方向只是当前迭代步骤的最优解；再宽泛一点：负梯度方向只是某迭代位置小范围内的局部最优解。
• 不具备二次终止性：在凸二次函数的凸优化问题，仅通过有限次迭代步骤，无法收敛至最优解。

在机器学习过程中，梯度下降法的时间复杂度同样不低。例如：

• 已知数据集$\mathcal{D}=\{x^{(i)},y^{(i)}{\}}_{i=1}^N$，使用极大似然估计作为目标函数进行描述，具体表示为：
  其中$\mathcal{L}(\cdot )$表示关于样本的损失函数;而$\mathcal{J}(\cdot )$才是最终的目标函数结果。
  $$\{\begin{array}{l}\mathcal{L}[x^{(i)},y^{(i)};\theta ]=-\log \mathcal{P}(y^{(i)}\mid x^{(i)};\theta )\\ \\ \begin{array}{rl}\mathcal{J}(\theta )& ={\mathbb{E}}_{(x^{(i)},y^{(i)})\in \mathcal{D}}\mathcal{L}[x^{(i)},y^{(i)};\theta ]\\ & =\frac{1}{N}\sum _{i=1}^N-\log \mathcal{P}(y^{(i)}\mid x^{(i)};\theta )\end{array}\end{array}$$
• 对目标函数$\mathcal{J}(\theta )$使用梯度下降法进行运算：
  牛顿-莱布尼兹公式~
  $$\begin{array}{rl}{\nabla }_{\theta }\mathcal{J}(\theta )& ={\nabla }_{\theta }\left[\frac{1}{N}\sum _{i=1}^N-\log \mathcal{P}(y^{(i)}\mid x^{(i)};\theta )\right]\\ & =\frac{1}{N}\sum _{i=1}^N{\nabla }_{\theta }\left[-\log \mathcal{P}(y^{(i)}\mid x^{(i)};\theta )\right]\end{array}$$
  很明显，可以发现：需要对每一个样本的目标函数结果对参数$\theta$计算梯度。该公式计算的时间复杂度为$\mathcal{O}(N)$，其中$N$表示数据集内样本数量。
• 但样本数量自身同样也是不可忽视的重要条件。机器学习反复出现的一个问题是：好的泛化需要大的训练集，但大的训练集的计算代价也很大。
  上述红色部分抄自《深度学习(花书)》$P_{94}$下端。

这明显出现了矛盾：既然想要降低梯度下降法的时间复杂度，就需要减少训练集样本数量$N$；但训练集样本数量的减少，也会导致该数据集对概率模型的泛化效果较差。

随机梯度下降

随机梯度下降方法的思想

随机梯度下降的核心在于，目标函数的梯度${\nabla }_{\theta }\mathcal{J}(\theta )$自身同样也是期望：
$$\begin{array}{rl}{\nabla }_{\theta }\mathcal{J}(\theta )& =\frac{1}{N}\sum _{i=1}^N{\nabla }_{\theta }\left[-\log \mathcal{P}(y^{(i)}\mid x^{(i)};\theta )\right]\\ & ={\mathbb{E}}_{(x^{(i)},y^{(i)})\in \mathcal{D}}\left[-\log \mathcal{P}(y^{(i)}\mid x^{(i)};\theta )\right]\end{array}$$
但期望同样可以使用小规模样本进行近似估计。在每一次迭代过程中，从训练集$\mathcal{D}$中均匀地抽取若干个独立同分布的小批量$(\text{Mini-Batch})$样本，通过计算批量内样本的梯度均值，并替代${\nabla }_{\theta }\mathcal{J}(\theta )$作为当前迭代步骤的梯度结果：
$${\nabla }_{\theta }\mathcal{J}(\theta )\approx \mathcal{G}=\frac{1}{m^{\prime }}\sum _{j=1}^{m^{\prime }}{\nabla }_{\theta }\mathcal{L}[x^{(i)},y^{(i)};\theta ]$$
我们发现：这种方法与随机森林中的$\text{Boostrapping}$采样方法有着异曲同工之妙。其中$\text{Boostrapping}$采样方法的采样集合${\mathcal{D}}^{\prime }$与原式集合$\mathcal{D}$中，如果$\mathcal{D}$中的样本数量趋近于无穷大，那么$\mathcal{D}‘$中始终不会从$\mathcal{D}$采样的概率是：
$$\underset{N\Rightarrow \infty }{\lim }(1-\frac{1}{N}{)}^N=\frac{1}{e}\approx 0.368$$
虽然在随机梯度下降中仅使用随机采样以获取小批量样本，但由于各迭代步骤产生的小批量样本均服从独立同分布，因而同样可以得到梯度的无偏估计。

随机梯度下降方法的步骤描述

关于随机梯度下降在第$k$个训练迭代的更新步骤表示如下：

初始化步骤：学习率${ϵ}_k$；初始参数$\theta$；

迭代过程：

• 事先判断准则是否满足条件(如目标函数结果小于某阈值$\delta$)$?$是，则算法终止；
• 从训练集$\mathcal{D}$中采出包含$m$个样本的小批量，记作${\mathcal{D}}^{\prime }$：
  $${\mathcal{D}}^{\prime }=\{(x^{(j)},y^{(j)}){\}}_{j=1}^m$$
• 针对该小批量的梯度$\mathcal{G}$进行估计：
  其中$f(\cdot )$则表示模型，那么$f(x^{(j)};\theta )$则表示模型关于$x^{(i)}$预测结果。
  $$\begin{array}{rl}\mathcal{G}& \Leftarrow {\mathbb{E}}_{(x^{(j)},y^{(j)})\in {\mathcal{D}}^{\prime }}\left[{\nabla }_{\theta }\mathcal{L}[f(x^{(j)};\theta ),y^{(j)}]\right]\\ & =\frac{1}{m}\sum _{j=1}^m{\nabla }_{\theta }\mathcal{L}[f(x^{(j)};\theta ),y^{(j)}]\end{array}$$
• 对参数$\theta$进行更新：
  $$\theta \Leftarrow \theta -ϵ\cdot \mathcal{G}$$
• 返回步骤$1$重新进行判断，直到算法终止为止。

关于学习率

一般情况下，随机梯度下降算法使用使用固定的学习率，在真实迭代过程中：有必要随着迭代步骤的推移逐渐降低学习率。我们记第$k$次迭代步骤的学习率结果为${ϵ}_k$；在实践过程中，给定初始学习率${ϵ}_0$，学习率衰减的迭代次数$\tau$；衰减系数$\alpha$，第$k$次迭代步骤的学习率${ϵ}_k$可表示为：
在该公式中，迭代步骤$k<\tau$；
$${ϵ}_k=(1-\alpha ){ϵ}_0+\alpha \cdot {ϵ}_{\tau }\alpha =\frac{k}{\tau }$$
这样得到学习率的效果是：在$\tau$次迭代步骤之前，学习率会呈现线性衰减；当迭代步骤$k>\tau$时，学习率呈现稳定状态。