红黑树 图文详解与代码实现
目录
（一）红黑树本质
1.1二叉搜索树
1.2近似平衡
1.3知识补充：
（二）红黑树原则
2.1红黑树法则
2.2红黑树的基本结构
2.3红黑树基的结构的几种常见形态
2.4红黑树单位节点的三叉链结构
（三）红黑树知识结构
1.原理图解
3.1.1插入的几种情况：
3.1.2情况1：树为空。
3.1.3 情况2：
3.1.4 情况3：
3.1.5 情况4：4-1
3.1.6 4-2情况
3.2 插入代码实现
3.2.1插入代码
3.2.2旋转代码：
（四）红黑树测试
4.1测试思路
（五）源码分享
如有错误请多多指正,感谢！！
研究工具：动画教学网站：
RedBlack.html · morris/Data-Structure-Visualizations - Gitee.comhttps://gitee.com/morris131/data-structure-visualizations/blob/master/RedBlack.html
红黑树的价值是什么？
红黑树被应用于数据结构map/set的封装的底层，也应用于Linux的数据内核，在进程调度CFS，虚拟内存管理，共享内存slab等场景都有广泛应用。
数据结构的角度看，（1）用于存储。无论数据是否平衡都可以在O（logN)的复杂度下完成 搜索、插入、删除操作。（2）用于排序。找到最小值和最大值
红黑树黑色和红色 也可看成两种状态，红黑区分的状态中，可以根据实际需求添加业务逻辑。
（一）红黑树本质
红黑树有两个关键词分别是，近似平衡和二叉搜索树。
1.1二叉搜索树
二叉树本身具有天然的查找优势，利用二分查找的原理，提高了查找效率。但是二叉搜索树在极端情况下，会退化成链表，查找效率很低。故我们通过约束”树的平衡“来保障树的查找效率。
1.2近似平衡
虽然平衡二叉树（AVL树）是完全平衡的，搜索效率达到了极致，但是插入等操作去维护树的平衡所需的消耗（指频繁的旋转操作）很大地降低了树的整体效率。因此，红黑树在性能上做了进一步优化，设计了“近似平衡”的原则。近似平衡，我的理解是，保证了黑色节点的完美平衡，至少就保证了50%以上的节点处于平衡，红黑交替，也限制了红色节点的平衡。
1.3知识补充：
（1）路径：从叶子节点沿着祖先路线往上找。
最长路径：一黑一红交替，且两者节点数量相等。
最短路径：全是黑色节点。
最长路径和最短路径的关系：最长路径不超过最短路径的二倍。
（2）RBTree的节点个数与高度
平衡二叉树（AVL树）O(N)=logN
黑色节点个数 2^h-1, 红色节点个数 【0，2^h-1】
总结点数 N=黑色节点个数+红色节点个数=【2^h-1,2^(h+1)-2】
<=>h（长）=log(N+2)-1 h(短）=log(N+1)
（3）效率比较；
红黑树 O(N)=2* logN+1 ==2* logN （数学归纳法证明，略）
AVL树 O(N)=logN
logN是常数级的时间复杂度，所以红黑树和平衡二叉树的复杂度可以近似相等。相比之下，红黑树的使用价值更高。
（二）红黑树原则
2.1红黑树法则
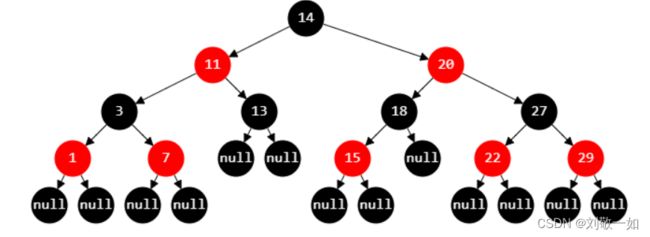
1.根节点是黑色。
2.对于一个节点，不是红色就是黑色。
3.对于一个红色节点，其两个子节点必须均为黑色。
4.每条路径上有数量相等的黑色节点。（黑色节点完美平衡）
5.认为叶子节点都是黑色。（NIL）
这是一颗红黑树：
2.2红黑树的基本结构
这是红黑树的单位结构，看做树的基（G,P,U,C组成)。
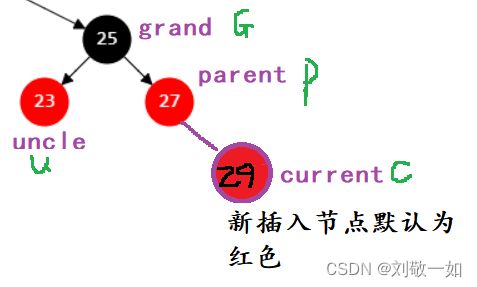红黑树的基
2.3红黑树基的结构的几种常见形态
红黑树调节平衡的方法有变色和旋转。根据颜色判断是否需要旋转。
但归根结底，我们还是需要根据插入时，基的形状来判断旋转和插入。三角关系通常伴随着双旋，三点一线常常需要单旋，根节点的处理也会比较特殊。空树认为只有一个空节点。
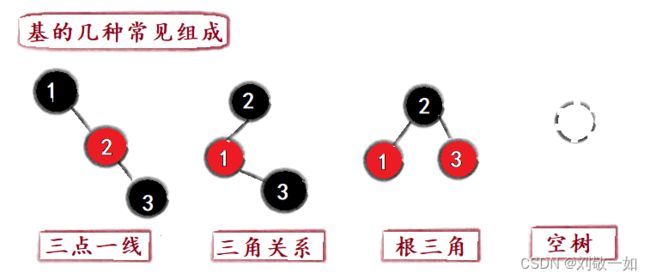基的几种常见组成
2.4红黑树单位节点的三叉链结构
在书写旋转代码时，要注意，红黑树节点是三叉链结构，两个节点之间的关系是由两根线连接起来的，修改一个节点的三个分叉时，也要记得改变原来与之相连的节点的指向。
enum Color
{
BLACK,
RED
};
template
class RBTreeNode
{
public:
RBTreeNode* _left;
RBTreeNode* _right;
RBTreeNode* _parent;
pair _kv;
Color _col;
RBTreeNode(const pair& kv)
:_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_kv(kv)
,_col(RED)//插入节点认为是红色
{}
}; 
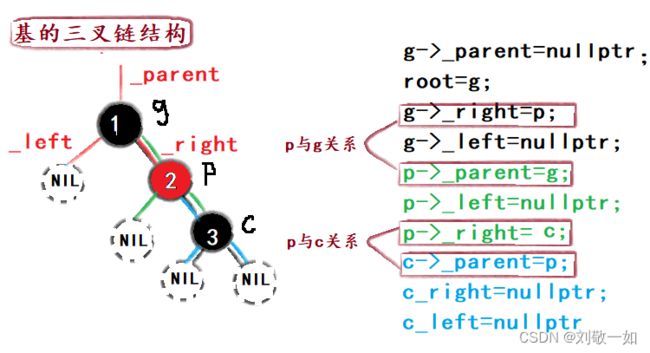基的三叉链结构
（三）红黑树知识结构
1.原理图解
3.1.1插入的几种情况：
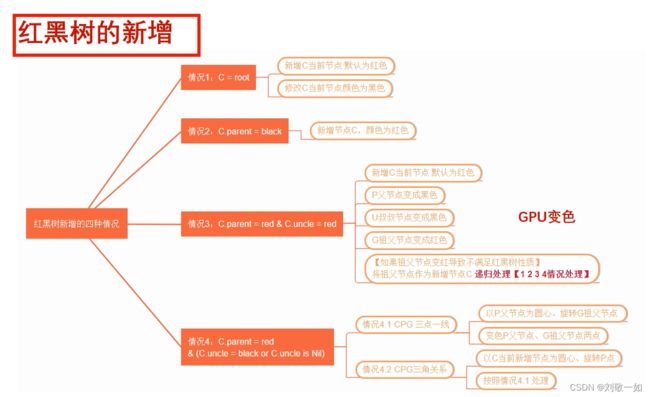插入功能的思路总览
3.1.2情况1：树为空。
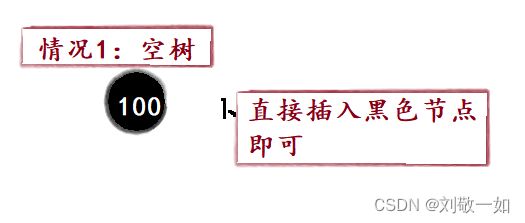情况1
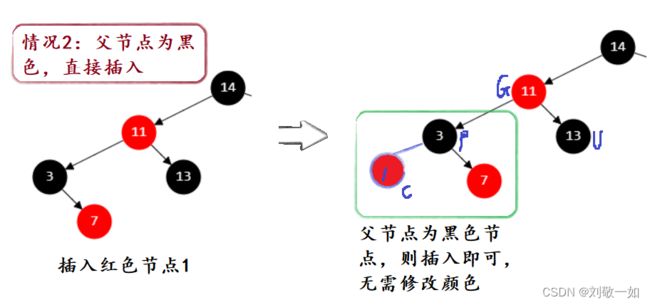3.1.3 情况2：
情况2
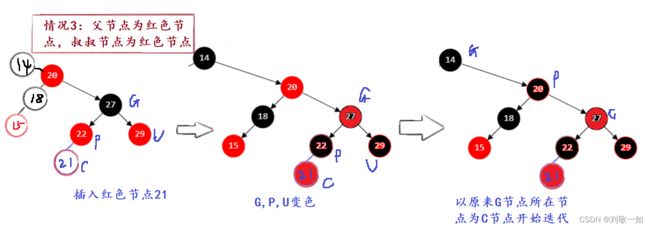3.1.4 情况3：
情况3
3.1.5 情况4：4-1
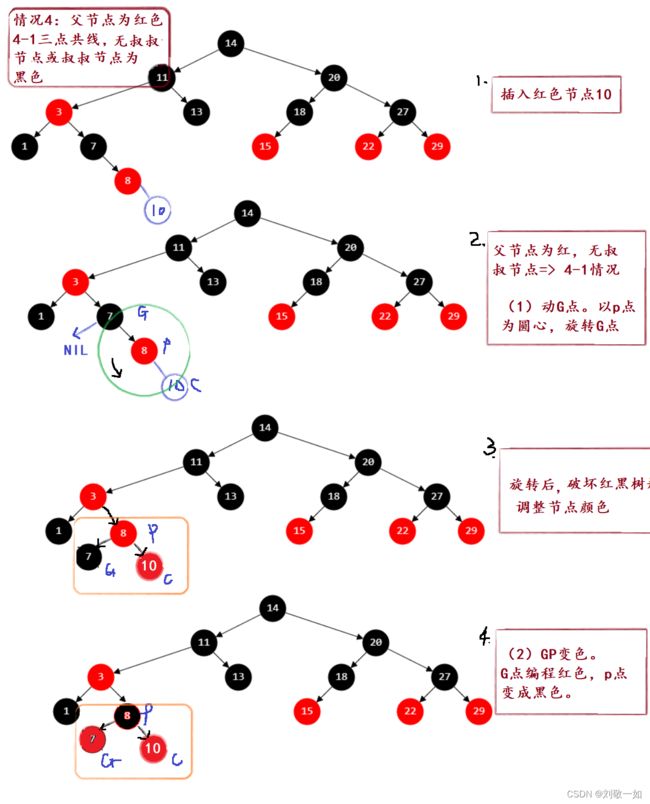情况4-1
3.1.6 4-2情况
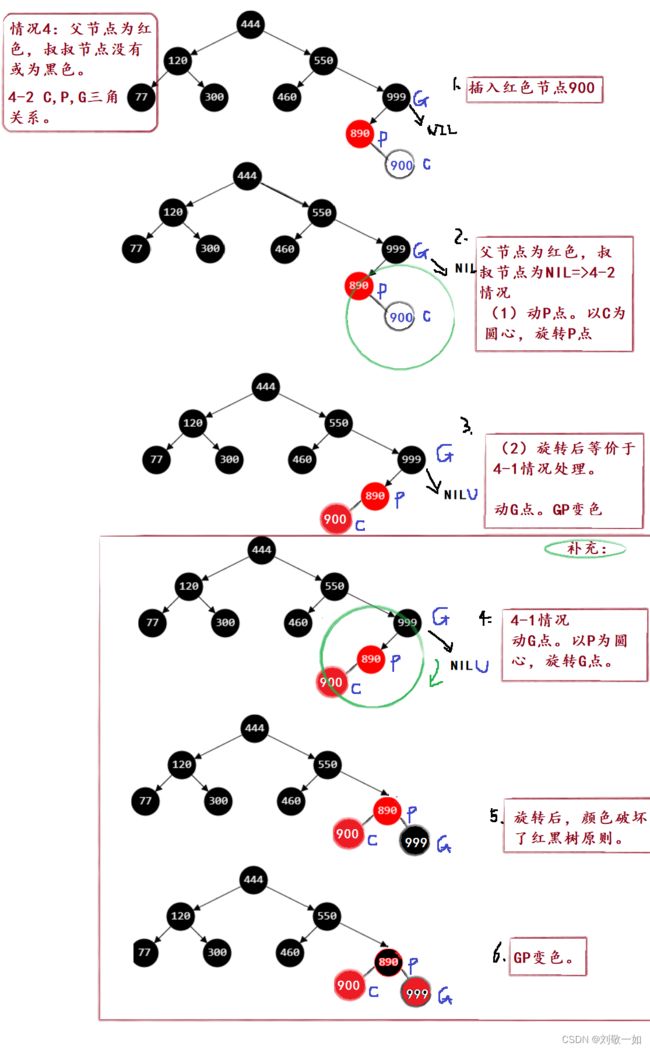情况4-2
3.2 插入代码实现
3.2.1插入代码
bool Insert(const pair &kv)
{
//情况1 空树
if (_root == nullptr)
{
Node* cur = new Node(kv);
cur->_col = BLACK; //变色
return true;
}
//树非空
Node* cur = _root;
Node* parent = cur;
while (cur)
{
if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else {
cout << "插入失败" << endl;
return false;
}
}
//找到了
cur = new Node(kv);
if (kv.first > parent->_kv.first)
{
parent->_right = cur;
cur->_parent = parent;
}
else {
parent->_left = cur;
cur->_parent = parent;
}
//调整相对平衡
//情况2 直接插入，无需变色
while(parent->_col==RED)
{
Node* grand = parent->_parent;
Node* uncle;
if (parent == grand->_right)
{
uncle = grand->_left;
}
else {
uncle = grand->_right;
}
//情况4 父节点红色，叔叔节点红（黑或无）
if (uncle->_col != RED)
{
//情况4-1 单旋 三点一线
if (grand->_right == parent && parent->_right == cur)
{
RotateL(grand); //左旋
grand->_col = RED;
parent->_col = BLACK; // G,P变色
}
else if (grand->_left == parent && parent->_left == cur)
{
RotateR(grand); //右旋
grand->_col = RED;
parent->_col = BLACK; //G，P变色
}
//情况4-2 双旋 三角关系
else if (grand->_left == parent && parent->_right == cur)
{
RotateL(parent);
//回到4-1
RotateR(grand);
grand->_col = RED;
cur->_col = BLACK; //现在排序 G-C-P 根绝GP变色，调整G,C，C为红色，C,G不同色，故G此时为黑色，调整为红色
}
else if (grand->_right == parent && parent->_left == cur)
{
RotateR(parent);
//回到4-1
RotateL(grand);
grand->_col = RED;
cur->_col = BLACK;
}
}
//情况3：父节点，叔叔节点均为红
else
{
uncle->_col = BLACK;//GPU变色
parent->_col = BLACK;
grand->_col = RED;
cur = grand;
parent = cur->_parent;
}
}
_root->_col = BLACK;
return true;
}
3.2.2旋转代码：
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if (subLR)
subLR->_parent = parent;
Node* ppNode = parent->_parent;
subL->_right = parent;
parent->_parent = subL;
if (parent == _root)
{
_root = subL;
subL->_parent = nullptr;
}
else
{
if (ppNode->_left == parent)
ppNode->_left = subL;
else
ppNode->_right = subL;
subL->_parent = ppNode;
}
}
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
if (subRL)
subRL->_parent = parent;/
Node* ppNode = parent->_parent;
subR->_left = parent;
parent->_parent = subR-
if (parent == _root)
{
_root = subR;
subR->_parent = nullptr;
}
else
{
if (ppNode->_left == parent)
{
ppNode->_left = subR;
}
else
{
ppNode->_right = subR;
}
subR->_parent = ppNode;
}
}（四）红黑树测试
4.1测试思路
红黑树的测试大的角度分为二叉搜索树测试和平衡性测试。二叉搜索树需要验证中序顺序。平衡性测试需要验证红黑树法则，其中红色节点不相连，和各路径黑色节点数目相等为主要测试。
4.2中序 有序测试
void InOrder()
{
_InOrder(head->parent); //通过观察控制台打印出数字是否为有序序列
cout << endl;
}
void _InOrder(Node* root)
{
if (root)
{
_InOrder(root->left);
cout << root->data << " ";
_InOrder(root->right);
}
}4.3平衡性测试
测试方法：
法则2： 根是否为黑 ------> 基本的if/else语句
法则3： 红色节点是否连续 ------> 当前红色节点的根节点是否为红色
法则4： 黑色节点数量是否相等 -----> 先通过一条路劲获得参照值，然后依次遍历每一条路径。
//法则3 ：检查是否出现了连续的红色节点
bool CheckRED_RED(Node* cur)
{
if (cur == nullptr)
{
return true;
}
if (cur->_col == RED && cur->_parent->_col == RED)
{
cout << "违反规则三，存在连续的红色节点" << endl;
return false;
}
return CheckRED_RED(cur->_left)
&& CheckRED_RED(cur->_right);
}
//法则4： 检查每条路径黑色节点的数量是否相等
bool CheckBlackNum(Node* cur, int blackNum, int benchmark) {
if (cur == nullptr) {
if (blackNum != benchmark) {
cout << "违反规则四：黑色节点的数量不相等" << endl;
return false;
}
return true;
}
if (cur->_col == BLACK)
++blackNum;
return CheckBlackNum(cur->_left, blackNum, benchmark)
&& CheckBlackNum(cur->_right, blackNum, benchmark);
}
bool IsBalance()//判断平衡性总函数
{
if (_root == nullptr)
{
return true;
}
if (_root->_col == RED)
{
cout << "根节点是红色，违反规则二" << endl;
return false;
}
// 算出最左路径的黑色节点的数量作为基准值
int benchmark = 0;
Node* cur = _root;
while (cur)
{
if (cur->_col == BLACK)
{
++benchmark;
}
cur = cur->_left;
}
int blackNum = 0;
return CheckRED_RED(_root) && CheckBlackNum(_root, blackNum, benchmark);
}（五）源码分享
数据结构_blog1: 学习笔记，每日成长 - Gitee.comhttps://gitee.com/liu-jingyiru/data-structure-blog1/tree/master/C++%E6%A8%A1%E6%8B%9F%E5%AE%9E%E7%8E%B0%E7%BA%A2%E9%BB%91%E6%A0%91