工业蒸汽量预测（速通二）

特征工程

特征工程就是从原始数据提取特征的过程。这些特征可以很好地描述数据。

特征工程的处理流程为首先去掉无用特征，去除冗余的特征，如共线特征，并利用存在的特征、转换特征、内容中的特征以及其他数据源生成新特征，然后对特征进行转换(数值化、类别转换、归一化等)，最后对特征进行处理(异常值、最大值、最小值，缺失值等)，以符合模型的使用。

简单来说，特征工程的处理一般包括数据预处理、特征处理、特征选择等工作，而特征选择视情况而定，如果特征数量较多，则可以进行特征选择等操作。

1.数据预处理和特征处理

1.1数据预处理

在进行特征提取之前，要对数据进行预处理，具体包括数据采集、数据清洗、数据采样。

数据采样：

数据在采集、清洗过以后，正负样本是不均衡的，故要进行数据采样。采样的方法有随机采样和分层抽样。但由于随机采样存在隐患，可能某次随机采样得到的数据很不均匀，因此更多的是根据特征进行分层抽样。

正负样本不平衡的处理方法:

正样本>负样本，且量都特别大的情况:采用下采样(downsampling)的方法。

正样本>负样本，且量不大的情况，可采用以下方法采集更多的数据:上采样(oversampling)，比如图像识别中的镜像和旋转;修改损失函数( loss function)设置样本权重。

1.2特征处理

特征处理的方法包括标准化、区间缩放法、归一化、定量特征二值化、定性特征哑编码、缺失值处理和数据转换。

归一化与标准化的使用场景:

●如果对输出结果范围有要求，则用归一化。

●如果数据较为稳定，不存在极端的最大值或最小值，则用归一化。

●如果数据存在异常值和较多噪声，则用标准化，这样可以通过中心化间接避免异常值和极端值的影响。

●支持向量机 (Support Vector Machine, SVM)、K近邻(K-Nearest Neighbor, KNN)、主成分分析(Principal Component Analysis, PCA)等模型都必须进行归一化或标准化操作。

定性特征哑编码：

哑变量( Dummy Variable)， 也被称为虚拟变量，通常是人为虚设的变量，取值为0或1,用来反映某个变量的不同属性。引入哑变量的目的是把原本不能定量处理的变量进行量化，从而评估定性因素对因变量的影响。

例如，假设变量“职业”的取值分别为工人、农民、学生、企业职员、其他等5种选项。那么我们则可以将“工人”定义为(0, 0, 0，1)、 “农民”定义为(0, 0, 1，0)、“学生”定义为(0, 1, 0, 0)、 “企业职员”定义为(1, 0, 0, 0)。

2.特征降维

2.1特征选择

特征选择是在数据分析和简单建模中最常用的特征降维手段。即映射函数直接将不重要的特征删除，不过这样会造成特征信息的丢失，不利于模型精度。由于数据分析以抓住主要影响因子为主，变量越少越有利于分析，因此特征选择常用于统计分析模型中:在超高维数据分析或者建模预处理中也会经常使用，如基因序列建模。特征选择的目标如表1-3-2 所示:

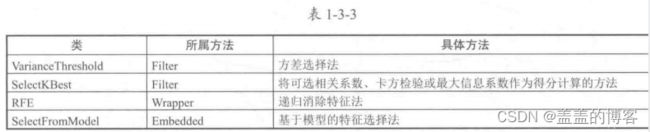
特征选择的方法有过滤法(Filter)、 包装法( Wrapper)和嵌入法( Embedded )。

●过滤法:按照发散性或者相关性对各个特征进行评分，通过设定阈值或者待选择阈值的个数来选择特征。

●包装法:根据目标函数(通常是预测效果评分)每次选择若干特征，或者排除若干特征。

●嵌入法:使用机器学习的某些算法和模型进行训练，得到各个特征的权值系数，并根据系数从大到小选择特征。这一方法类似于过滤法， 区别在于它通过训练来确定特征的优劣。

#  特征相关性
plt.figure(figsize=(20,16))
column = train_data_scaler.columns

mcorr = train_data_scaler[column].corr(method='spearman')  # 相关性

# 特征降维       (相关性筛选)
mcorr = mcorr.abs()
numerical_corr = mcorr[mcorr['target']>0.1]['target']   # 筛选>0.1的特征变量, 并只显示特征变量
numerical_corr.sort_values(ascending=False)  # 从大到小排序

2.2多重共线性分析

多重共线性分析的原则是特征组之间的相关性系数较大，即每个特征变量与其他特征变量之间的相关性系数较大，故可能存在较大的共线性影响，这会导致模型估计不准确。因此,后续要使用PCA对数据进行处理，去除多重共线性。

2.3线性降维

线性降维常用的方法有主成分分析法和线性判别分析法。

主成分分析法

#  PCA 处理    （除去数据的多重共线性）
from sklearn.decomposition import PCA

pca = PCA(n_components=0.9)   # 保持90%的信息

new_train_pca = pca.fit_transform(train_data_scaler.iloc[:,0:-1])
new_test_pca = pca.fit_transform(test_data_scaler)
# pd.DataFrame(new_train_pca).describe()

线性判别分析法

模型训练

1回归模型训练和预测

回归模型训练和预测的步骤:

(1)导入需要的工具库。

(2)对数据预处理，包括导入数据集、处理数据等操作，具体为缺失值处理、连续特征归一化、 类别特征转换等。

(3)训练模型。选择合适的机器学习模型，利用训练集对模型进行训练，达到最佳拟合效果。

(4)预测结果。将待预测的数据集输入到训练好的模型中，得到预测结果。

2线性回归模型

分为一元线性回归模型，多元线性回归模型。

调用方法：

# 切分数据
# 用PCA保留16维特征数据
new_train_pca_16 = new_train_pca_16.fillna(0)
train = new_train_pca_16[new_test_pca_16.columns]
target = train_data['target']

# 切分数据
train_data,test_data,train_target, test_target = train_test_split(train,target, test_size=0.2, random_state=0)

# 多元线性回归
clf = LinearRegression()
clf.fit(train_data, train_target)
mse = mean_absolute_error(test_target, clf.predict(test_data))
linear_predict = clf.predict(test_data)

优点:模型简单，部署方便，回归权重可以用于结果分析:训练快。

缺点:精度低，特征存在一定的共线性问题。

使用技巧:需要进行归一化处理，建议进行一定的特征选择，尽量避免高度相关的特征同时存在。

本题结果:效果一般，适合分析使用。

3K近邻回归模型

K近邻算法不仅可以用于分类，还可以用于回归。

优点:模型简单，易于理解，对于数据量小的情况方便快捷，可视化方便。

缺点:计算量大，不适合数据量大的情况:需要调参数。

使用技巧:特征需要归一化，重要的特征可以适当加一定比例的权重。

本题结果:效果一般。

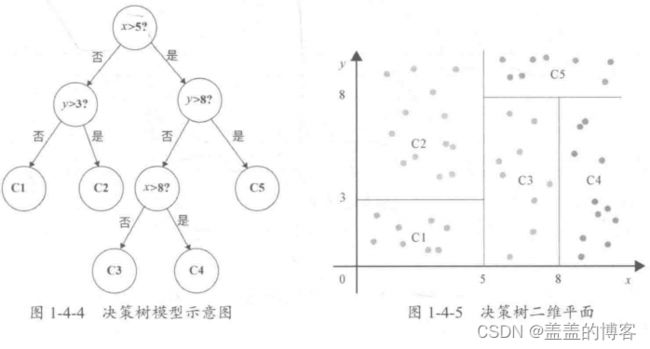
4决策树回归模型

决策树回归可以理解为根据一定准则，将二个空间划分为若干个子空间，然后利用子空间内所有点的信息表示这个子空间的值。对于测试数据，我们只要按照特征将其归到某个子空间，便可得到对应子空间的输出值。

我们可以利用这些划分区域的均值或者中位数代表这个区域的预测值，一旦有样本点按划分规则落入某一个区域，就直接利用该区域的均值或者中位数代表其预测值。

5集成回归模型

随机森林回归模型

随机森林就是通过集成学习的思想将多棵树集成的一种算法，基本单元是决策树，而它的本质属于机器学习的一个分支——集成学习( Ensemble Learning)。

在回归问题中，随机森林输出所有决策树输出的平均值。

随机森林回归模型的主要优点:在当前所有算法中，具有极好的准确率；能够有效地运行在大数据集上；能够处理具有高维特征的输入样本，而且不需要降维；能够评估各个特征在分类问题上的重要性；在生成过程中，能够获取到内部生成误差的一种无偏估计；对于缺省值问题也能够获得很好的结果。

# 随机森林回归
clf3 = RandomForestRegressor(n_estimators=400)
clf3.fit(train_data,train_target)
mse2 = mean_absolute_error(test_target, clf3.predict(test_data))
RandomForest_predict = clf3.predict(test_data)

优点:使用方便，特征无须做过多变换;精度较高;模型并行训练快。

缺点:结果不容易解释。

使用技巧:参数调节，提高精度。

本题结果:比较适合。

LightGBM回归模型

# LGB模型回归
clf2 = lgb.LGBMRegressor(learning_rate=0.01,
                       max_depth=-1,
                       n_estimators=5000,
                       boosting_type='gbdt',
                       random_state=2022,
                       objective='regression')
clf2.fit(X=train_data, y=train_target,eval_metric='MSE',verbose=50)
mse3 = mean_absolute_error(test_target, clf2.predict(test_data))

print('LinearRegression的测试集的MSE得分为：{}'.format(mse))
print('RandomForestRegressor的测试集的MSE得分为：{}'.format(mse2))
print('LGBMRegressor的测试集的MSE得分为：{}'.format(mse3))
LGB_predict = clf2.predict(test_data)

可自行尝试运行，可能需要几分钟时间。

优点:精度高。

缺点:训练时间长，模型复杂。

使用技巧:有效的验证集防止过拟合;参数搜索。

本题结果:适用。

其他常用模型

弹性网络( Elastic Net)回归是在参数空间中对L1和L2范数进行正则化的线性回归模型，可以理解为是下面要介绍的岭回归和Lasso回归的结合，其主要用在正则化融合的技术中。

model ='ElasticNet'
metal_models[model] = ElasticNet()

param_grid = {'alpha': np.arange(1e-4,1e-3,1e-4),
              'l1_ratio': np.arange(0.1,1.0,0.1),
              'max_iter':[100000]}

metal_models[model], cv_score, grid_results = train_model(metal_models[model], param_grid=param_grid, X=metal_x_train,y=metal_y_train,
                                              splits=splits, repeats=1)

cv_score.name = model
score_models = score_models.append(cv_score)

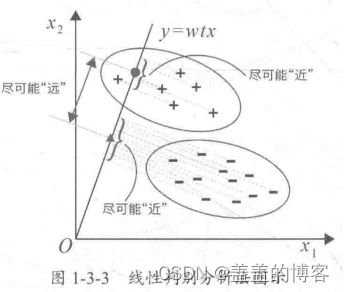
SVR (Support Vector Regression)是支持向量机在线性回归模型中的应用。支持向量机大家都比较熟悉，其主要用于分类。这类模型的优势主要是在采用核函数之后，可以进行自动升维拟合，提高拟合效果，并且参数计算量并没有增加。

模型验证

1模型评估的概念和方法

1.1欠拟合与过拟合

1.2模型的泛化与正则化

泛化是指机器学习模型学习到的概念在处理训练未遇到过的样本时的表现，即模型处理
新样本的能力。

正则化(Regularization) 是给需要训练的目标函数加上一些规则(限制)，目的是为了防止过拟合。

岭回归和LASSO回归

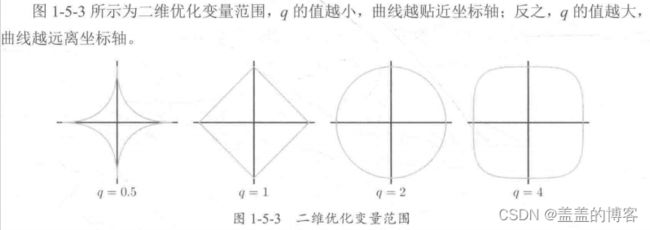
在原始的损失函数后添加正则项，可以减小模型学习到的θ的大小，这样可以使模型的泛化能力更强。相对应地，对参数空间进行L2范数正则化的线性模型称为岭回归( Ridge Regression)；

对参数空间进行L1范数正则化的线性模型则称为LASSO回归(LASSO Regression)。

岭回归和LASSO回归的不同之处:

(1)使用岭回归改进的多项式回归算法，随着a的改变，拟合曲线始终是曲线，直到最后变成一条几乎水平的直线;也就是说，在使用岭回归之后，多项式回归算法在模型变量前还是有系数的，因此很难得到一条斜的直线。

(2) 而使用LASSO回归改进的多项式回归算法，随着a的改变，拟合曲线会很快变成一条斜的直线，最后慢慢变成一 条几乎水平的直线，即模型更倾向于一条直线。

model = 'Lasso'

metal_models[model] = Lasso()
alph_range = np.arange(1e-4,1e-3,4e-5)
param_grid = {'alpha': alph_range}

metal_models[model], cv_score, grid_results = train_model(metal_models[model], param_grid=param_grid, X=metal_x_train,y=metal_y_train,
                                              splits=splits, repeats=repeats)

cv_score.name = model
score_models = score_models.append(cv_score)

plt.figure()
plt.errorbar(alph_range, abs(grid_results['mean_test_score']),abs(grid_results['std_test_score'])/np.sqrt(splits*repeats))
plt.xlabel('alpha')
plt.ylabel('score')

model = 'Ridge'

metal_models[model] = Ridge()
alph_range = np.arange(0.25,6,0.25)
param_grid = {'alpha': alph_range}

metal_models[model],cv_score,grid_results = train_model(metal_models[model], param_grid=param_grid, X=metal_x_train,y=metal_y_train,
                                              splits=splits, repeats=repeats)

cv_score.name = model
score_models = score_models.append(cv_score)

plt.figure()
plt.errorbar(alph_range, abs(grid_results['mean_test_score']),
             abs(grid_results['std_test_score'])/np.sqrt(splits*repeats))
plt.xlabel('alpha')
plt.ylabel('score')

1.3回归模型的评估指标

回归模型的评估有平均绝对值误差、均方误差、均方根误差和R平方值四种方法。

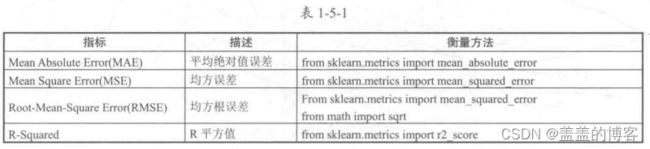
1.4交叉验证

常用的交叉验证方法包括简单交叉验证、K折交叉验证、留一法交叉验证和留P法交叉验证。

简单交叉验证

K折交叉验证

留一法交叉验证

留P法交叉验证

其他交叉验证分割方法：基于类标签，具有分层的交叉验证。用于分组数据的交叉验证。时间序列分割。

2模型调参

2.1调参

可能影响Random Forest 和Gradient Tree Boosting模型性能的参数。

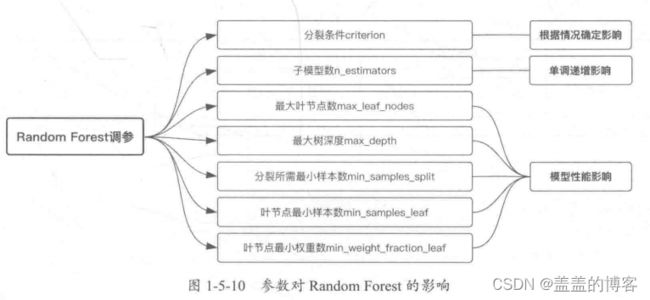
2.2网格搜索

网格搜索(Grid Search) 是一种穷举搜索的调参手段。在所有候选的参数选择中，通过循环遍历，尝试每一种可能性，表现最好的参数就是最终的结果。其原理就像是在数组中找最大值。

以有两个参数的模型为例，参数a有3种可能，参数b有4种可能，把所有可能性列出来，可以表示成一个3*4的表格，其中每个单元就是一个网格，循环过程就像是在每个网格中遍历、搜索，因此得名网格搜索。

#  # 使用数据训练随机森林模型，采用网格搜索方法调参
from sklearn.model_selection import GridSearchCV
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import train_test_split

model = 'linear_predict'

train_data, test_data, train_target, test_target = train_test_split(train, target, test_size=0.2, random_state=0)
randomForestRegression = RandomForestRegressor()
parameters = {'n_estimators':[50,100,200], 'max_depth':[1,2,3]}
clf = GridSearchCV(randomForestRegression, parameters, cv=5)
clf.fit(train_data, train_target)
score_test = mean_squared_error(test_target, clf.predict(test_data))

print('调参后的RandomForest_Regressor的训练集得分：{}'.format(clf.score(train_data,train_target)))
print('调参后的RandomForest_Regressor的测试集得分：{}'.format(clf.score(test_data,test_target)))
print("RandomForest模型调参前MSE：{}".format(mse))
print("RandomForest模型调参后MSE：{}".format(score_test))

2.3随即参数优化

# 使用数据训练随机森林模型，采用随机参数优化方法调参
from sklearn.model_selection import RandomizedSearchCV
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import train_test_split 

train_data, test_data, train_target, test_target =train_test_split(train, target, test_size=0.2, random_state=0)
randomForestRegressior = RandomForestRegressor()
parameters = {'n_estimators':[50, 100, 200, 300], 'max_depth':[1,2,3,4,5]}
clf = RandomizedSearchCV(randomForestRegressior, parameters, cv=5)
clf.fit(train_data, train_target)
score_test = mean_squared_error(test_target, clf.predict(test_data))

print('调参后的RandomForest_Regressor的训练集得分：{}'.format(clf.score(train_data,train_target)))
print('调参后的RandomForest_Regressor的测试集得分：{}'.format(clf.score(test_data,test_target)))
print("RandomForest模型调参前MSE：{}".format(mse))
print("RandomForest模型调参后MSE：{}".format(score_test))

2.4LGB模型调参

# lgb模型调参
clf = lgb.LGBMRegressor(num_leaves=31)
parameters = {'learning_rate':[0.01,0.1,1],'n_estimators':[20,40]}
clf= GridSearchCV(clf, parameters, cv=5)
clf.fit(train_data, train_target)
score_test = mean_squared_error(test_target, clf.predict(test_data))

print('调参后的LGB的训练集得分：{}'.format(clf.score(train_data,train_target)))
print('调参后的LGB的测试集得分：{}'.format(clf.score(test_data,test_target)))
print("LGB模型调参前MSE：{}".format(mse))
print("LGB模型调参后MSE：{}".format(score_test))

2.5学习曲线与验证曲线

学习曲线是在训练集大小不同时，通过绘制模型训练集和交叉验证集上的准确率来观察模型在新数据上的表现，进而判断模型的方差或偏差是否过高，以及增大训练集是否可以减小过拟合。

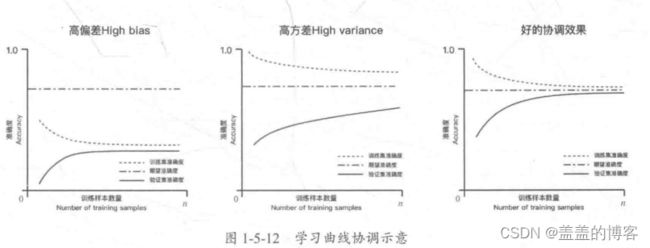
和学习曲线不同，验证曲线的横轴为某个超参数的一系列值，由此比较不同参数设置下(而非不同训练集大小)模型的准确率。