C++【2023.3.25-2023.8.12】力扣刷题——1.数组篇

力扣刷题指南

（若有侵权会及时删除，请联系告知！）

第一题

453. 最小操作次数使数组元素相等

题目描述

给你一个长度为 n 的整数数组，每次操作将会使 n - 1 个元素增加 1 。返回让数组所有元素相等的最小操作次数。

示例

示例1：
输入：nums = [1,2,3]
输出：3
解释：
只需要3次操作（注意每次操作会增加两个元素的值）：
[1,2,3]  =>  [2,3,3]  =>  [3,4,3]  =>  [4,4,4]

示例2：
输入：nums = [1,1,1]
输出：0

思路分析

• 知识点：数组的改变、移动
• 一个长度为n的整数数组，每次操作都会使$n-1$个元素增加1，此时我们不需要考虑数组的绝对大小，而需要考虑每个元素的相对大小的变化，于是，我们可以将其反向理解，认为每次操作都会使1个元素减少1。
• 为了符合题目的条件，我们只需要将每个元素的值达到最小值即可，即计算
  $$\sum _{i=0}^{n-1}(nums[i]-min(nums))$$

示例代码

class Solution {
public:
    int minMoves(vector<int>& nums) {
        int minValue = *min_element(nums.begin(),nums.end());
        int sum = 0;
        for(int i = 0; i < nums.size(); i++)
        {
            sum += (nums[i] - minValue);
        }
        return sum;
    }
};

复杂度分析

• 时间复杂度：$O(n)，$,其中n为数组中的元素数量。首先遍历求出最小值，再次遍历计算操作次数。
• 空间复杂度：$O(1)。$

第二题

665. 非递减数列

题目描述

给你一个长度为 $n$ 的整数数组$nums$，请你判断在最多改变 1 个元素的情况下，该数组能否变成一个非递减数列。

我们是这样定义一个非递减数列的： 对于数组中任意的 $i$, $(0<=i<=n-2)$，总满足 $nums[i]<=nums[i+1]$。

示例

示例1：
输入: nums = [4,2,3]
输出: true
解释: 你可以通过把第一个 4 变成 1 来使得它成为一个非递减数列。

示例2：
输入: nums = [4,2,1]
输出: false
解释: 你不能在只改变一个元素的情况下将其变为非递减数列。

思路分析（参考评论区码不停题的思路解决的）

• 知识点：数组的改变、移动
• 根据题目要求我们可以得知：最多只能有一个满足nums[i] > nums[i + 1],虽然数列[3,4,1,2]是符合这个条件的，但是它无论怎么修改都不是非递减数列，因此，我们还要修改其中的一个值，然后继续判断它是否是非递减数列。
• 我们可以来看以下三个例子【4、2、3】、【-1、4、2、3】、【2、3、3、2、4】，通过分析上面三个例子可以发现，当我们发现后面的数字小于前面的数字产生冲突后：
  （1）有时候需要修改前面较大的数字（比如前两个例子需要修改4），
  （2）有时候却要修改后面较小的数字（比如第三个例子需要修改2），
  那么有什么内在规律吗？是有的，判断修改哪个数字其实跟再前面一个数的大小有关系

1. 例子1中，当i指向2时，它再前面的数不存在（比如4前面没有数字了），我们直接修改前面的数字为当前的数字2即可。
2. 例子2中，当前面的数字存在，并且小于当前数时，-1小于2，我们仍修改前面的数字（4）为当前数字2。即a[i-1] = a[i]
3. 例子3中，（3,3,2）如果再前面的数字大于当前数（例子3），我们需要将当前数2改为前面的数3。即a[i] = a[i-1]

示例代码

class Solution {
public:
    bool checkPossibility(vector<int>& nums) {
        if (nums.size() <= 1) {
		    return true;
	    }
        int count = 0;

        for(int i = 1; i < nums.size() && count < 2; i++)
        {
            if(nums[i - 1] <= nums[i]) 
                continue;
            count++;
            if(i - 2 >= 0 && nums[i - 2] > nums[i])
                nums[i] = nums[i - 1];
            else
                nums[i - 1] = nums[i]; 
        }
            return count <= 1;
    }
};

复杂度分析

• 时间复杂度：$O(n)，$,其中n为数组中的元素数量。
• 空间复杂度：$O(1)。$

第三题

283. 移动零

题目描述

给定一个数组 $nums$，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

请注意 ，必须在不复制数组的情况下原地对数组进行操作。

示例

示例1：
输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]

示例2：
输入: nums = [0]
输出: [0]

思路分析——参考题解

• 知识点：双指针法、快速排序
• 根据题目要求，我们可以创建两个指针 $i$ 和 $j$，在第一次遍历时指针 $j$ 用来记录当前有多少个非0元素。即遍历的时候每遇到一个非0元素就进行交换处理，将其放置在左边的非0子数组里，第一次遍历完后，$j$ 指针的下标就指向了最后一个非0元素下标。
• 第二次遍历时，起始位置从 $j$ 开始到结束，将剩下的这段区域内的元素全部置为0。
• 此题还可以利用快速排序的思想进行一次遍历，参考动画演示 283.移动零

示例代码

class Solution {
public:
    void moveZeroes(vector<int>& nums) {
        int i = 0,j = 0;
        for(int i = 0; i < nums.size(); i++)
        {
            if(nums[i] != 0)
            nums[j++] = nums[i];
        }
        while(j < nums.size())
        nums[j++] = 0;
    }
};

复杂度分析

• 时间复杂度：$O(n)，$,其中n为数组中的元素数量。
• 空间复杂度：$O(1)。$

第四题

53. 最大子数组和

题目描述

给你一个整数数组 $nums$ ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。
子数组是数组中的一个连续部分。（注意跟子序列区分）

示例

示例1：
输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

示例2：
输入：nums = [1]
输出：1

示例3：
输入：nums = [5,4,-1,7,8]
输出：23

思路分析——参考经典动态规划：最大子数组问题

• 知识点：数组、动态规划—线性dp
• 为了得到合适的状态转移方程。对于这类子数组问题，我们需要重新定义dp数组的含义：
• 以$nums[i]$为结尾的最大子数组为$dp[i]$
• 这种定义之下，若想要得到整个数组的最大子数组和，不能直接返回$dp[n-1]$，而需要遍历整个$dp$数组。
  
• 如何从$dp[n-1]$推导到$dp[n]$呢？
• 答：要么自己作为子数组，要么跟前面的子数组拼凑在一起，然后取最大值，即
• 

示例代码

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int n = nums.size();
        int *dp = new int[n];
        dp[0] = nums[0];
        for(int i = 1; i < nums.size(); i++)
        {
            dp[i] = max(nums[i],nums[i] + dp[i - 1]);
        }
        int res = -9999999999;
        for(int i = 0; i < nums.size(); i++)
        {
            res = max(res,dp[i]);
        }
        return res;
    }
};

复杂度分析

• 时间复杂度：$O(n)，$,其中n为数组中的元素数量。
• 空间复杂度：$O(n)。$可以考虑用变量代替数组，直接将空间复杂度降为$O(1)$

第五题（第四题的进阶）

1749. 任意子数组和的绝对值的最大值

题目描述

给你一个整数数组 nums 。一个子数组 $[num{s}_l,num{s}_{l+1},...,num{s}_{r-1},num{s}_r]$的和的绝对值为 $abs(numsl+numsl+1+...+numsr-1+numsr)$。
请你找出 $nums$ 中和的绝对值最大的任意子数组（可能为空），并返回该最大值 。
$abs(x)$定义如下：
如果 $x$ 是负整数，那么 $abs(x)=-x$。
如果 $x$ 是非负整数，那么 $abs(x)=x$。

示例

示例1：
输入：nums = [1,-3,2,3,-4]
输出：5
解释：子数组 [2,3] 和的绝对值最大，为 abs(2+3) = abs(5) = 5 。

示例2：
输入：nums = [2,-5,1,-4,3,-2]
输出：8
解释：子数组 [-5,1,-4] 和的绝对值最大，为 abs(-5+1-4) = abs(-8) = 8 。

思路分析——参考经典动态规划：最大子数组问题

• 求子数组绝对值最大值，要么是子数组的最大值，要么是子数组的最小值，在第四题的基础上进行二重动态规划。

示例代码

class Solution {
public:
    int maxAbsoluteSum(vector<int>& nums) {
        int n = nums.size();
        int *plus_dp = new int[n];
        int *minus_dp = new int[n];
        //base case
        plus_dp[0] = nums[0];
        minus_dp[0] = nums[0];
        for(int i = 1; i < nums.size(); i++)
        {
            plus_dp[i] = max(nums[i],nums[i] + plus_dp[i - 1]);
            minus_dp[i] = min(nums[i], nums[i] + minus_dp[i - 1]);
        }
        int res1 = -999999999;
        int res2 = 9999999999;
        for(int i = 0; i < nums.size(); i++)
        {
            res1 = max(res1,plus_dp[i]);
            res2 = min(res2,minus_dp[i]);
        }
        res1 = abs(res1);
        res2 = abs(res2);
        if(res1 >= res2)
            return res1;
        else
            return res2;
    }
};

复杂度分析

• 时间复杂度：$O(n)，$,其中n为数组中的元素数量。
• 空间复杂度：$O(n)。$可以考虑用变量代替数组，直接将空间复杂度降为$O(1)$

第六题

189. 轮转数组

题目描述

给定一个整数数组 $nums$ ，将数组中的元素向右轮转 $k$ 个位置，其中 $k$ 是非负数。

示例

示例1：
输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]

示例2：
输入：nums = [-1,-100,3,99], k = 2
输出：[3,99,-1,-100]
解释: 
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]

思路分析——参考官方题解

具体介绍环状替换和数组翻转算法

环状替换算法

• 首先从下标 $0$ 开始遍历，最后又回到起点 $0$ ，这个过程走了 $a$ 圈（$a$为正整数），每圈的长度为 $n$。例如在示例$[1,2,3,4,5,6,7],k=3$中，第一轮走了$1，4，7，3，6，2，5，1$，总共走了 $3$ 圈。
• 在这个过程中，走的每一步的长度为$k$，一共走过了$b$个元素，例如在示例$[1,2,3,4,5,6],k=2$中，第一轮走了$1,3,5,1$，一共走了三个元素，所以走的总步长为 $bk$ ，也就是这 $a$ 圈的长度。即 $an=bk$。
• 则 $an$ 一定为 $n，k$ 的公倍数，又因为我们需要在第一次回到起点时就要结束，所以 $a$ 要最小，所以 $an$ 就是 $n$ 和 $k$ 的最小公倍数 $lcm(n,k)$ 。因此 $b$ 就为$lcm(n,k)/k$，所以从起点再次回到起点的过程中就会访问到$lcm(n,k)/k$ 个元素。为了访问到所有的元素，我们需要进行遍历的次数为，$n/lcm(n,k)/k=n\ast k/lcm(n,k)=gcd(n,k)$（最大公约数和最小公倍数的关系），即需要遍历的次数为 $n$ 和 $k$ 的最大公约数。
• 在示例 $[1,2,3,4,5,6],k=2$中，需要走两轮才能把所有的元素遍历完毕，分别为$[1,3,5][2,4,6]$

示例代码

class Solution {
public:
    void rotate(vector<int>& nums, int k) {
        int n = nums.size();
        k = k % n;
        int count = gcd(n,k);
        for(int start = 0; start < count; start++)
        {
            int current = start;
            int prev = nums[start];
            do{
                int next = (current + k) % n;
                swap(nums[next],prev);
                current = next;
            }while(start != current);
        }
    }
};

复杂度分析

• 时间复杂度：$O(n)，$,其中n为数组中的元素数量。
• 空间复杂度：$O(1)$

数组翻转算法

参考美服的翻转算法，原地址

nums = "----->-->"; k =3
result = "-->----->";

reverse "----->-->" we can get "<--<-----"
reverse "<--" we can get "--><-----"
reverse "<-----" we can get "-->----->"
this visualization help me figure it out :)

示例代码

class Solution {
public:
    void reverse(vector<int>& nums, int start, int end) {
        while (start < end) {
            swap(nums[start], nums[end]);
            start += 1;
            end -= 1;
        }
    }

    void rotate(vector<int>& nums, int k) {
        k %= nums.size();
        reverse(nums, 0, nums.size() - 1);
        reverse(nums, 0, k - 1);
        reverse(nums, k, nums.size() - 1);
    }
};

复杂度分析

• 时间复杂度：$O(n)，$,其中n为数组中的元素数量。每个元素被翻转两次，一共n个元素，因此总时间复杂度为O(2n) = O(n)。
• 空间复杂度：$O(1)。$

第七题

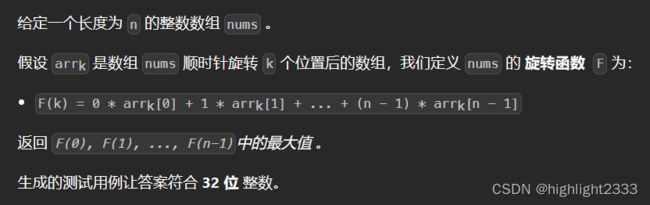
396.旋转函数

题目描述

示例

示例1：
输入: nums = [4,3,2,6]
输出: 26
解释:
F(0) = (0 * 4) + (1 * 3) + (2 * 2) + (3 * 6) = 0 + 3 + 4 + 18 = 25
F(1) = (0 * 6) + (1 * 4) + (2 * 3) + (3 * 2) = 0 + 4 + 6 + 6 = 16
F(2) = (0 * 2) + (1 * 6) + (2 * 4) + (3 * 3) = 0 + 6 + 8 + 9 = 23
F(3) = (0 * 3) + (1 * 2) + (2 * 6) + (3 * 4) = 0 + 2 + 12 + 12 = 26
所以 F(0), F(1), F(2), F(3) 中的最大值是 F(3) = 26 。

示例2：
输入: nums = [100]
输出: 0

思路分析——动态规划，题解出自[官方题解]

-

示例代码

class Solution {
public:
    
    int maxRotateFunction(vector<int>& nums) {
        int n = nums.size();
        int sum = 0;
        int total = 0;
        //int *dp = new int[n];
        int dp_0 = 0;
        int dp_1 = 0;
        for(int i = 0; i < n; i++)
        {
            total += nums[i];
            sum += i * nums[i];
        }
        dp_0 = sum;
        int maxValue = dp_0;
        for(int k = 1; k < n; k++)
        {
            dp_1 = dp_0 + total - n * nums[n - k];
            dp_0 = dp_1;
            maxValue = max(maxValue,dp_0);

            //cout << dp[k] << endl;
        }

        return maxValue;
    }
};

复杂度分析

• 时间复杂度：$O(n)$，其中n为数组中的元素数量。
• 空间复杂度：$O(1)$，仅使用常数空间。

第八题

88. 合并两个有序数组
题目要求算法复杂度为$O(m+n)$

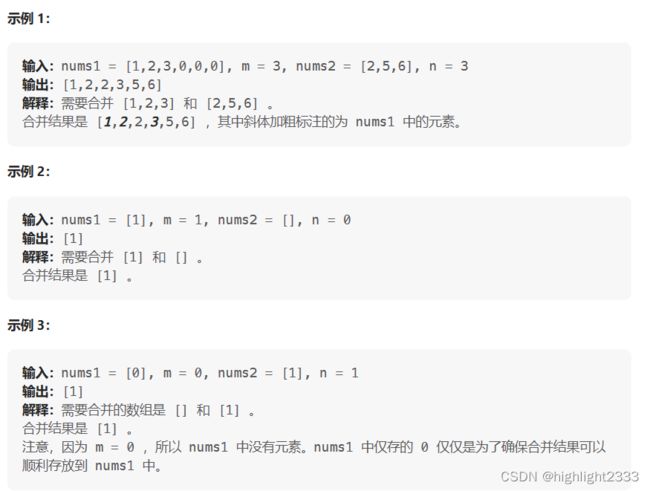
题目描述

示例

思路分析（双指针法）

思路一：直接在nums1容器中添加元素，最后进行遍历
思路二：(双指针法)由于nums1与nums2已经被排序，我们可以将两个数组看作队列，每次从两个数组头部取出比较小的数字放到结果中。于是我们分别设置m和n为两个数组的头部指针，实例代码如下：

思路二示例代码

class Solution {
public:
    void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
        int *ans = new int[m + n];
        int i = 0, j = 0,k = 0;
        while(i < m || j <  n)
        {
            if(i == m)
            {
                ans[k++] = nums2[j++];    
            }
            else if(j == n)
            {
                ans[k++] = nums1[i++];    
            }
            else if(nums1[i] <= nums2[j])
            {
                ans[k++] = nums1[i++];
            }
            else if(nums1[i] > nums2[j])
            {
                ans[k++] = nums2[j++];
            }
        }
        for(int i = 0; i < m + n; i++)
        {
            nums1[i] = ans[i];
        }
    }
};

思路三：由于 $nums1$ 的后半部分为空，可以直接覆盖而不会影响结果。因此可以指针设置为从后向前遍历，每次取两者之中的较大者放进 $nums1$ 的最后面。由于填补一个空格之后又多出来一个空格，因此示例代码如下：

复杂度分析

• 时间复杂度：$O(m+n)$，其中m,n为数组中的元素数量。
• 空间复杂度：$O(m+n)$，建立了中间数组。

思路三示例代码

class Solution {
public:
    void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
        int tail = m + n - 1;
        m--;
        n--;
        while(m >= 0 || n >= 0 )
        {
            if(m < 0)
            {
                nums1[tail--] = nums2[n--];
            }
            else if(n < 0)
            {
                nums1[tail--] = nums1[m--];
            }
            else if(nums1[m] >= nums2[n])
            {
                nums1[tail--] = nums1[m--];
            }
            else if(nums1[m] < nums2[n])
            {
                nums1[tail--] = nums2[n--];
            }
        }
    }
};

复杂度分析

• 时间复杂度：$O(m+n)$，其中m,n为数组中的元素数量。
• 空间复杂度：$O(1)，直接对nums1原地修改，不需要额外空间。$